5 인과모형

c(
  "rio", "tidyverse", "tidytable", "psych", "psychTools", 
  "skimr", "janitor", "tidymodels", "lm.beta", "mediation",
  "GGally", "ggforce", "mdthemes", "patchwork", "ggdag",
  "r2symbols", "equatiomatic", "gt" 
  ) -> pkg 
sapply(pkg, function(x){
  if(!require(x, ch = T)) install.packages(x, dependencies = T)
  library(x, ch = T)
})

5.1 통계의 착시

착시(visual illusion)는 우리가 알고 있는 세상은 세상 그 자체가 아니라 우리 마음 속에 비친 그림자임을 보여주는 좋은 예다. 착시는 시각적 대상을 모호한 방식으로 표현함으로써, 보는 사람의 지각, 기억 등의 주관적인 경험이 그 대상에 대한 인식이 달라지도록 한다. 사물을 관찰하는 방향, 맥락, 측정수준(미시 vs. 거시) 등에 따라 다양한 사례가 제시돼 있다 (안도현 2021).

가장 유명한 착시 중 하나가 16세기 이탈리아 화가 주세페 알침볼도의 그림이다 (Figure 5.1). 왼쪽의 그림은 과일, 꽃 등을 묘사한 평범한 정물화이나, 뒤짚어 놓은 오른쪽 그림에서는 정물 뿐 아니라 사람의 얼굴도 나타난다. 요소 하나 하나를 미시 수준에서 보면 과일 등의 사물이고, 개별 요소를 연결해 거시 수준에서 보면 얼굴이 된다.

Reversible Head With Basket of Fruit (circa 1590) by Giuseppe Arcimboldo

Figure 5.1: Reversible Head With Basket of Fruit (circa 1590) by Giuseppe Arcimboldo

착시는 매우 흥미로운 현상이기 때문에 다양한 착시가 만들어져 있다. 매년 착시 경연대회도 열린다. 주세페 알침볼도처럼 착시를 이용해 작품활동을 하는 예술가도 적지 않다.

5.1.1 상관성의 착시

착시의 사례는 시각적으로 특수하게 구성한 것에 국한되지 않는다. 자연현상과 사회현상에 모두 시각 착시와 같은 착시현상이 있다. 실제로는 원인과 결과의 결과과 아닌데도 원인과 결과의 관계라고 착각하는 인과착시가 그 예다.

원인과 결과에 대해서는 모든 사람들이 직관적으로 알고 있다. 밥을 먹으니 배가 부르고, 치료를 받고 병에서 낫고, 공부를 해서 실력을 쌓는 등의 현상을 보며, 인과관계를 추론한다. 그런데, 과연 우리의 눈에 명확하게 원인과 결과의 관계라고 보고 느끼는 것들이 정말로 원인과 결과의 관계일까?

원인과 결과의 관계인 것처럼 명백해 보이는 것들이 실은 원인과 결과의 관계가 아닌 착시인 경우가 적지 않다. 예를 들어보자. 아동기에는 발의 크기와 계산능력 사이에 양의 상관성이 있다. 발이 큰 아이일수록 계산을 더 잘한다. 그렇다면, 발이 크면 계산능력이 높다고 할수 있을까?

5.1.2 심슨의 역설

상관성의 착시로 대표적인 예가 심슨의 역설(Simpson’s paradox)이다. 전체로 보았을 때 나타나는 상관관계의 방향성이 전체를 이루는 요소로 나눠 보면 반대 방향으로 나타난다 (Simpson 1951). 예를 들어, 인구 전체로 보면 변수X와 변수Y 사이에 양의 상관관계가 있지만, 이를 각 요소(예, 남성과 여성)으로 구분하면, 상관관계가 반대방향으로 나타나는 현상이다 (Kievit et al. 2013).

저그마을에서 보양제와 기력의 관계를 연구중인 갑돌이를 통해 심슨의 역설을 살펴보자.

5.1.2.1 가져오기

갑돌이는 저그들이 보양제를 먹었기 때문에 기력이 좋아지는지 확인하기 위해 보양제를 복용한 남성저그 100명과 여성저그 100명을 대상으로 복용량과 기력을 측정한 자료를 수집했다 (가상의 데이터셋을 만들어 갑돌이의 저그마을 자료를 갈음하자.)

set.seed(37)
male_v <- rnorm(100, 170, 15)
female_v <- rnorm(100, 140, 15)
noise <- rnorm(100, 15, 8)

# 남성 데이터프레임 생성
male_df <- data.frame(
  # 복용량
  dose = male_v, 
  # 복용량과 역관계의 기력
  vigor = 300 - (male_v * .7) + noise,
  # 남성 값 100개 생성
  sex = rep("남성", 100)
  )
# 여성 데이터프레임 생성
female_df <- data.frame(
  # 복용량
  dose = female_v, 
  # 복용량과 역관계의 기력
  vigor = 200 - (female_v * .7) + noise,
  # 여성 값 100개 생성
  sex = rep("여성", 100)
  )
# 남성과 여성 데이터프레임 행(row))뱡향(아래 위로) 결합 
df <- bind_rows(male_df, female_df)
# 생성한 데이터 프레임 살펴보기
glimpse(df)
## Rows: 200
## Columns: 3
## $ dose  <dbl> 171.8713, 175.7311, 178.6886, 165.5938, 157.5748, 165.0093, 167.~
## $ vigor <dbl> 183.8075, 196.7337, 179.6053, 187.6091, 199.4402, 213.0087, 206.~
## $ sex   <chr> "남성", "남성", "남성", "남성", "남성", "남성", "남성", "남성", ~

생성한 데이터셋은 200행 3열의 데이터프레임이다. 즉, 200명에 대해 변수 3개(복용량, 기력, 성)로 이뤄진 데이터프레임이다.

상관분석을 해보자. 복용량과 기력 사이에는 양의 상관성이 있다. 상관계수 \(r\)은 .45로서 적지 않은 수준의 상관성이 나타난다.

cor(df$dose, df$vigor)
## [1] 0.4512355

회귀분석을 하면 회귀계수가 복용량 1단위 증가할때 기력은 .94단위 증가한다. 결정계수는 0.2다. 보양제 복용이 기력증가의 20%를 설명한다. 갑돌이는 보양제가 기력을 높여준다고 결론을 내려도 될까?

df %>% lm(vigor ~ dose, .) %>% summary()
## 
## Call:
## lm(formula = vigor ~ dose, data = .)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -97.658 -28.184  -2.538  28.158 101.139 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   9.3439    20.7672   0.450    0.653    
## dose          0.9446     0.1328   7.115    2e-11 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 38.34 on 198 degrees of freedom
## Multiple R-squared:  0.2036, Adjusted R-squared:  0.1996 
## F-statistic: 50.62 on 1 and 198 DF,  p-value: 2.004e-11

결론을 내리기 앞서 두 변수의 관계를 시각화해보자.

cor(df$dose, df$vigor) %>% round(2) -> title_r
lm(vigor ~ dose, df)$coef[2] %>% round(2) -> title_b
df %>% ggplot(aes(dose, vigor)) + 
  geom_point(col = "deep pink") +     
  geom_smooth(method = lm, se = F) +  
  labs(
    title = str_glue("복용량과 기력의 관계(*r* = {title_r}, *B* = {title_b})")
    ) +
  # mdthemes패키지로 ggplot2에서 마크다운 문법 사용
  md_theme_gray() 
## `geom_smooth()` using formula 'y ~ x'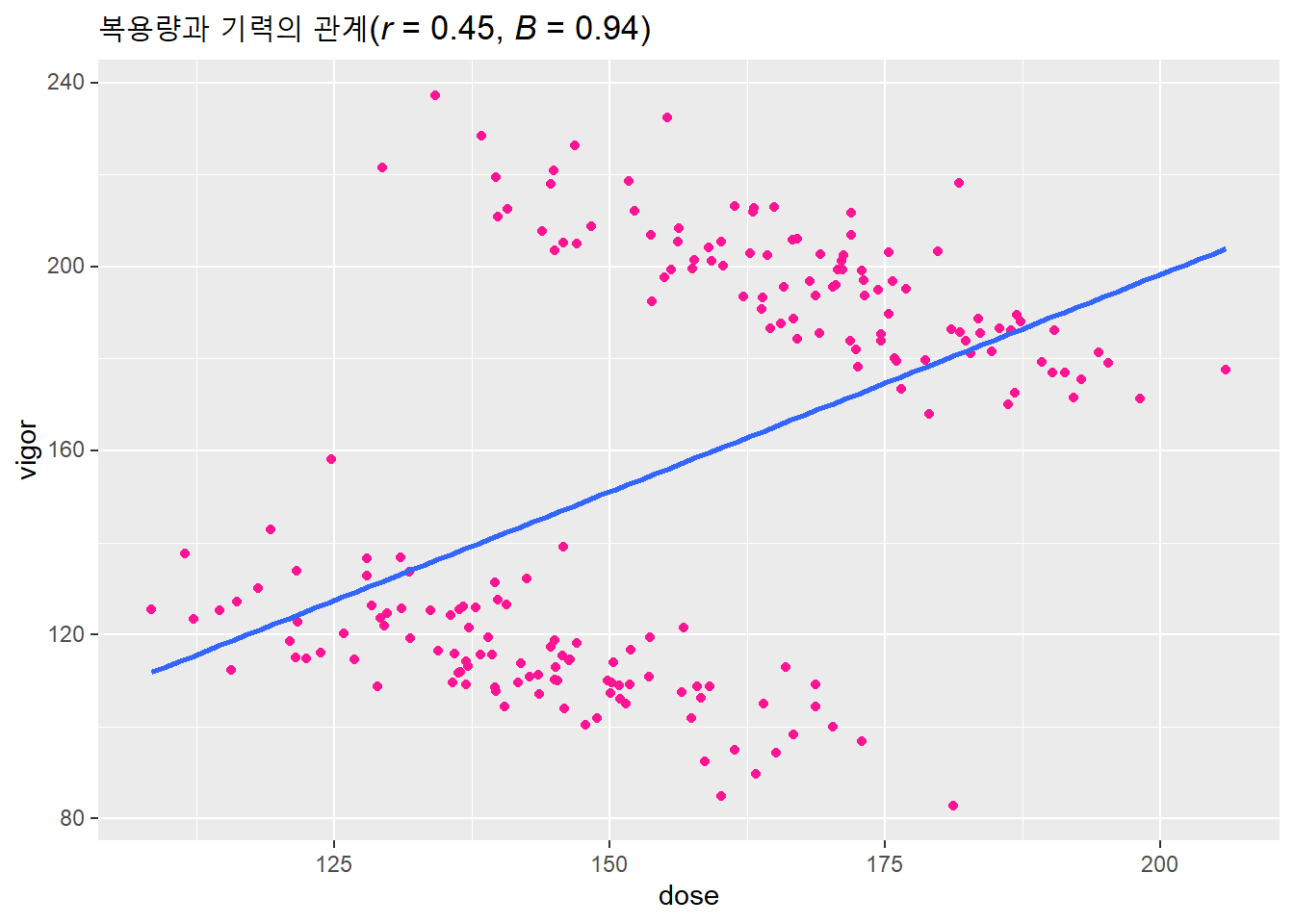

복용량과 기력 사이에 양의 상관성이 존재하는 것은 분명하지만, 분포를 보면 복용량을 늘린다고 기력이 좋아진다고 결론을 내릴 수는 없는 것처럼 보인다.

왜 이런 문제가 나타난 것일까? 거시와 미시수준의 차이에서 오는 착시 때문이다. 미시 수준에서 관찰해 개별 요소의 상관관계와 거시 수준에서 요소와 요소를 연결한 상관관계가 달리 나타난 것이다.

남성과 여성을 구분해 시각화해보자. 앞에서는 변수는 복용량(dose), 기력(vigor)를 각각 X축과 Y축에 투입했는데, 추가로 성(sex)을 제3변수로(색으로 지정)로서 투입하자.

# sex를 색으로써 세번째 변수로 투입
df %>% ggplot(aes(dose, vigor, color = sex)) + 
  geom_point(col = "deep pink") +           
  geom_smooth(method = lm, se = F) +
  labs(
    title = "복용량과 기력의 관계(남성과 여성)"
    ) + theme(plot.title = element_text(size = 20)) 
## `geom_smooth()` using formula 'y ~ x'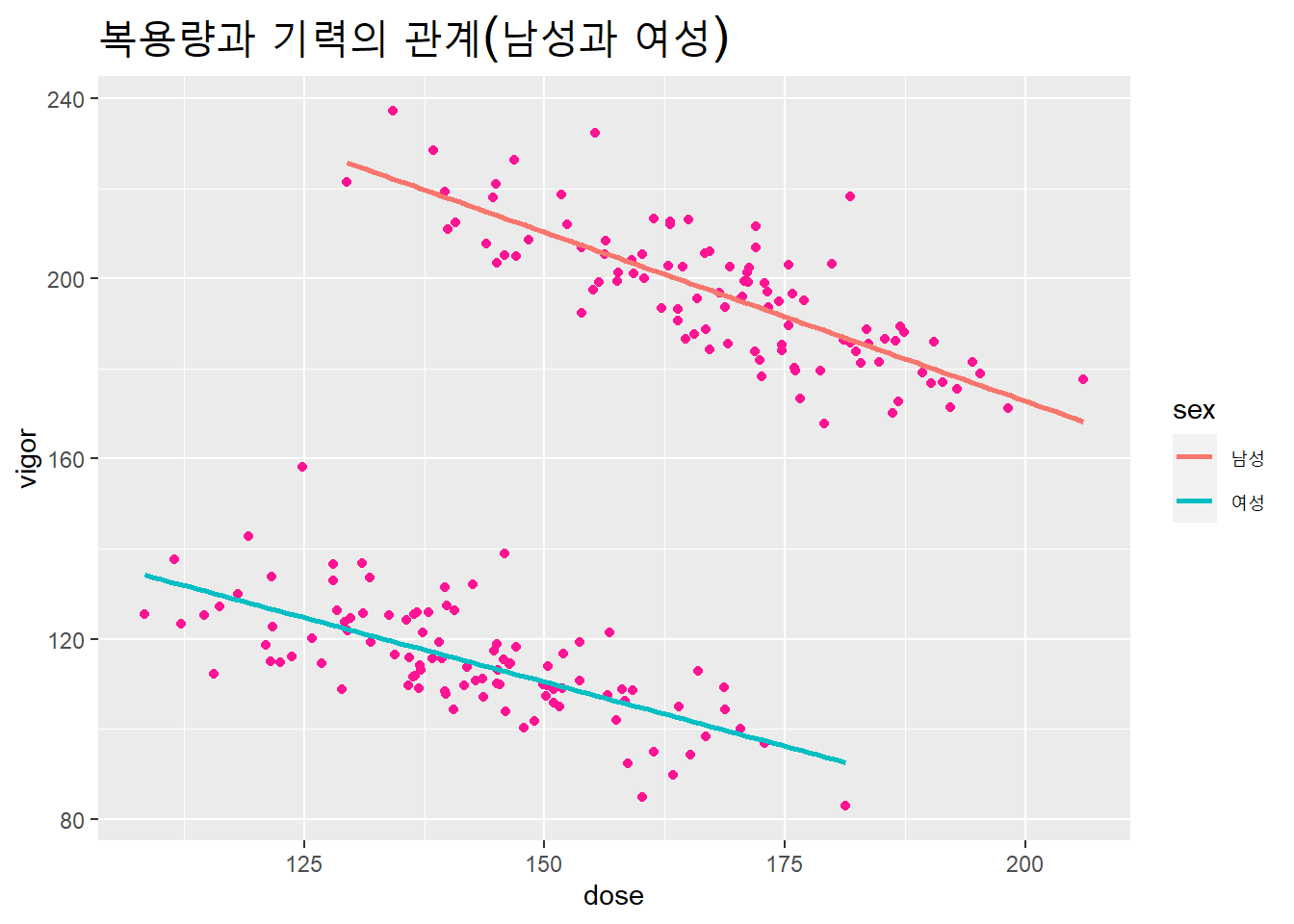

남성과 여성으로 구분해 분석하면 복용량과 기력 사이에 음의 상관성이 나타난다. 즉, 보양제를 복용하면 오히려 기력이 감소한다. 그럼에도 전체적으로 복용량과 기력 사이에 양의 상관성이 나타나는 이유는 무엇일까?

다양한 설명이 가능하지만, 한가지 가능한 설명은 남성이 여성보다 기력이 좋은데 보양제도 여성보다 더 많이 먹기 때문이다. 즉, 성을 제3변수로서 통제하면 복용량과 기력 사이의 요인별 관계를 드러낼 수 있다.

제3변수 sex의 역할은 dose만 독립변수로 투입한 단순회귀모형 모형1과 dose와 함께 sex를 통제변수로 투입한 다중회귀모형 모형2를 통해 확인할 수 있다.

더미변수(dummy variable)

sex는 속성이 남성과 여성으로 이뤄진 범주형 변수다. 범주형 변수는 회귀분석에 직접 투입할 수 없기 때문에 범주의 속성을 0 혹은 1의 숫자형으로 변환해 투입한다. 이처럼 범주형 변수로 된 독립변수의 속성을 0과 1로 변환한 변수를 더미변수(가변수 또는 지시변수)라고 한다.

lm()함수는 범주형 변수를 자동으로 일련의 더미변수(가변수)를 생성한다. levels()함수를 사용할때 알파벳순서로 0과 1로 취급한다. 예를 들어, 성의 속성을 남성과 여성으로 코딩한 경우, 알파벳 순서가 남성-여성의 순서이므로, 남성은 0, 여성은 1로 바꿔 계산한다.

c("남성", "남성", "여성", "여성") %>% 
  factor() %>% levels()
## [1] "남성" "여성"

만일 성의 속성을 male과 female로 코딩한 경우, 알파벳 순서가 female-male의 순서이므로, female은 0, male은 1로 바꿔 계산한다.

c("male", "male", "female", "female") %>% 
  factor() %>% levels()
## [1] "female" "male"

혼동을 피하고 싶으면 mutate()함수로 속성을 0과 1로 변경한다.

data.frame(sex = c("male", "male", "female", "female")) %>% 
  mutate(sex1 = recode(sex,
                     male = 0,
                     female = 1))
##      sex sex1
## 1   male    0
## 2   male    0
## 3 female    1
## 4 female    1

더미변수가 포함된 회귀모형은 다음과 같다.

data.frame(
  dv = 1:4,
  sex = c("남성", "남성", "여성", "여성")) %>% 
  lm(dv ~ sex,.) %>% extract_eq()

\[ \operatorname{dv} = \alpha + \beta_{1}(\operatorname{sex}_{\operatorname{여성}}) + \epsilon \]

회귀계수 \(\beta_{1}\)의 의미는 남성 대비 여성인 경우의 종속변수 dv의 평균변화량이다. 남성의 값이 0이고, 여성의 값이 1이므로 여성이라는 것은 sex변수가 1단위 증가하는 것과 같다.

사용자 함수mod_two()를 만들어 회귀모형 2개를 생성하자.

names(df)
## [1] "dose"  "vigor" "sex"
y <- 2
x1 <- 1      # vigor ~ dose
xx <- c(1,3) # vigor ~ dose + sex
nn <- length(xx) + 1

### 회귀모형 2개 생성
mod_two <- function(df, y, x1, xx) {
## 변수 및 회귀모형
  # 변수
  dv <- names(df)[y]
  iv1 <- names(df)[x1]
  iv2 <- names(df)[xx]
  # 모형1 회귀식
  fml_mdl1 <- iv1 %>%
    paste0(., collapse = " + ") %>%
    paste0(dv, " ~ ", .)
  # 모형2 회귀식
  fml_mdl2 <- iv2 %>%
    paste0(., collapse = " + ") %>%
    paste0(dv, " ~ ", .)
## 회귀분석 + 데이터프레임결합
  model <- c(fml_mdl1, fml_mdl2)
  return(model)
}
mod_two(df, y, x1, xx) -> model
data.frame(Formulas = model) %>% gt()
Formulas
vigor ~ dose
vigor ~ dose + sex

생성한 모형 2개를 사용자함수 reg_f()를 만들어 모형의 개수만큼 회귀분석한다.

### 회귀분석 사용자함수
reg_f <- function(nn, model){  
  # 표의 행 개수: 모형2 변수 + 절편행 개수
  output <- list()
  for (i in seq_along(model)) {
    fit <- df %>% lm(model[i], .)
    # 변수명, 회귀계수, 표준오차 데이터프레임
    op <- tidy(fit)[1:nn, 1:3] %>% 
      # 표준화 회귀계수 데이터프레임
      bind_cols.(tidy(lm.beta(fit))[1:nn, 2]) %>%
      # 결정계수 데이터프레임
      bind_rows.(data.frame(
        term = c("결정계수",
                 "수정결정계수"),
        estimate...2 = NA,
        std.error = c(summary(fit)$r.squared,
                         summary(fit)$adj.r.squared),
        estimate...4 = NA
      ))
    output <- list(output, op)
  }
  return(output)
}
reg_f(nn, model) -> fit
fit
## [[1]]
## [[1]][[1]]
## list()
## 
## [[1]][[2]]
## # A tidytable: 5 x 4
##   term         estimate...2 std.error estimate...4
##   <chr>               <dbl>     <dbl>        <dbl>
## 1 (Intercept)         9.34     20.8          9.34 
## 2 dose                0.945     0.133        0.945
## 3 <NA>               NA        NA           NA    
## 4 결정계수           NA         0.204       NA    
## 5 수정결정계수       NA         0.200       NA    
## 
## 
## [[2]]
## # A tidytable: 5 x 4
##   term         estimate...2 std.error estimate...4
##   <chr>               <dbl>     <dbl>        <dbl>
## 1 (Intercept)       308.       7.20        308.   
## 2 dose               -0.664    0.0423       -0.664
## 3 sex여성           -99.0      1.73        -99.0  
## 4 결정계수           NA        0.955        NA    
## 5 수정결정계수       NA        0.954        NA

분석결과 2개를 결합해 표로 정리한다. 사용자함수 tbl_two()를 만들자.

### 모형 2개 결합해 표로 정리
tbl_two <- function(df, fit){
  fit[[1]][[2]] %>%
    bind_cols.(fit[[2]]) %>%
    select.(term = term...5, # 모형2 변수명
            estimate...2:estimate...8) %>%
    gt() %>%
    tab_header(str_glue("{names(df)[y]}에 대한 회귀분석결과")) %>%
    fmt_number(-1, decimals = 2) %>%
    fmt_missing(-1, missing_text = html("<br>")) %>%
    cols_label(
      term = md("IV"),
      estimate...2 = md("_B_"),
      std.error...3 = md("_SE_"),
      estimate...4 = html("&beta;"),
      estimate...6 = md("_B_"),
      std.error...7 = md("_SE_"),
      estimate...8 = html("&beta;"),
    ) %>%
    tab_spanner(
      label = "Model 1",
      columns = estimate...2:estimate...4) %>%
    tab_spanner(
      label = "Model 2",
      columns = estimate...6:estimate...8) %>%
    text_transform(
      locations = 
        cells_body(
          columns = term,
          rows = term == "결정계수"),
         fn = function(x) {html(
          "<p align='center'><em>R<sup>2</sup></em></p>")        }) %>% 
    text_transform(
      locations = 
        cells_body(
          columns = term,
          rows = term == "수정결정계수"),
      fn = function(x) {html(
          "<p align='center'><em>R<sup>2</sup><sub>adj</sub></em></p>")
        }) %>% 
    tab_footnote(
      footnote = str_glue("N = {nrow(df)}"),
      locations = cells_title()
    )
}
tbl_two(df, fit)
vigor에 대한 회귀분석결과1
IV Model 1 Model 2
B SE β B SE β
(Intercept) 9.34 20.77 9.34 308.32 7.20 308.32
dose 0.94 0.13 0.94 −0.66 0.04 −0.66
sex여성


−99.02 1.73 −99.02

R2
0.20

0.95

R2adj
0.20

0.95
1 N = 200

vigor에 대해 dose만을 단독으로 독립변수로 투입한 모형1에서는 회귀계수가 0.94이나, sex를 통제변수로 투입한 모형2에서는 dose의 회귀계수가 -0.66으로 바뀌었다. sex를 통제하지 않으면, 복용량이 증가할수록 기력이 증가하나, sex를 통제하면 복용량이 증가할수도록 기력이 감소한다.

복용량과 기력의 관계에서 가능한 혼란변수는 성뿐 아니라 다양한 변수(나이, 인종, 교육수준, 생활습관 등)가 있을 수 있다.

5.2 통계적 유의성

우리가 알고 있는 세상이 우리 마음 속에 비친 그림자인것처럼, 우리 분석하기 위해 수집한 자료는 세상의 실제를 그대로 반영한 결과는 아니다. 세상의 실제에서 일부를 ’추출’한 것에 불과하다. 통계용어로 연구대상이 되는 실제를 모집단(population)이라 하고, 모집단의 일부를 추출한 것을 표본(sample)이라 한다. 모집단에서 표본을 추출하는 것을 표집(sampling)이라 한다.

  • 추론통계(inferential statistics)
    표본을 통해 모집단에 대해 추론하는 통계방법
  • 기술통계(descriptive statistics)
    표본의 자료를 기술해 요약하는 통계방법

표본을 통해 모집단을 추론할 때는 표본의 분석결과가 모집단에 대해 정확히 반영하는 정도를 확률적으로 판단할 수 밖에 없다. 이 판단을 통계적 유의성 검정이라 한다. 유의성 검정은 \(p\)값(통계적 유의도: statistical significance)을 이용한다.

\(p\)값은 측정한 통계치의 발생확률로서 분석결과를 통해 얻은 통계치가 우연에 의한 것인지 여부에 대한 지표다. \(p\)값은 확률적인 지표이므로 유의확률이라도고 한다.

\(p\)값이 0.05라면 통계치가 우연일 확률이 5% 정도 된다는 의미다. 즉, 100번 표집했을 때 5번 정도는 우연하게 그러한 결과가 나타날 수 있고, 95번은 우연이 아니라 모형에 부합하는 결과일수 있다는 의미다. 따라서 \(p\)값이 작으면 작을수록 우연이 아닐 가능성, 즉 분석결과가 모형에 부합할 가능성이 높아진다.

관행적으로 \(p\)값 0.05를 우연성 여부의 판단기준으로 사용하고 있다. 이 판단기준을 유의수준(알파: \(\alpha\))라고 한다. \(p\)값 0.05미만이면 통계치 옆에 \(*\)표식을 달고, “통계적으로 유의하다”고 표현한다.(\(p\)값이 0.01미만이면 \(**\), 0.001미만이면 \(***\)으로 표시한다.)

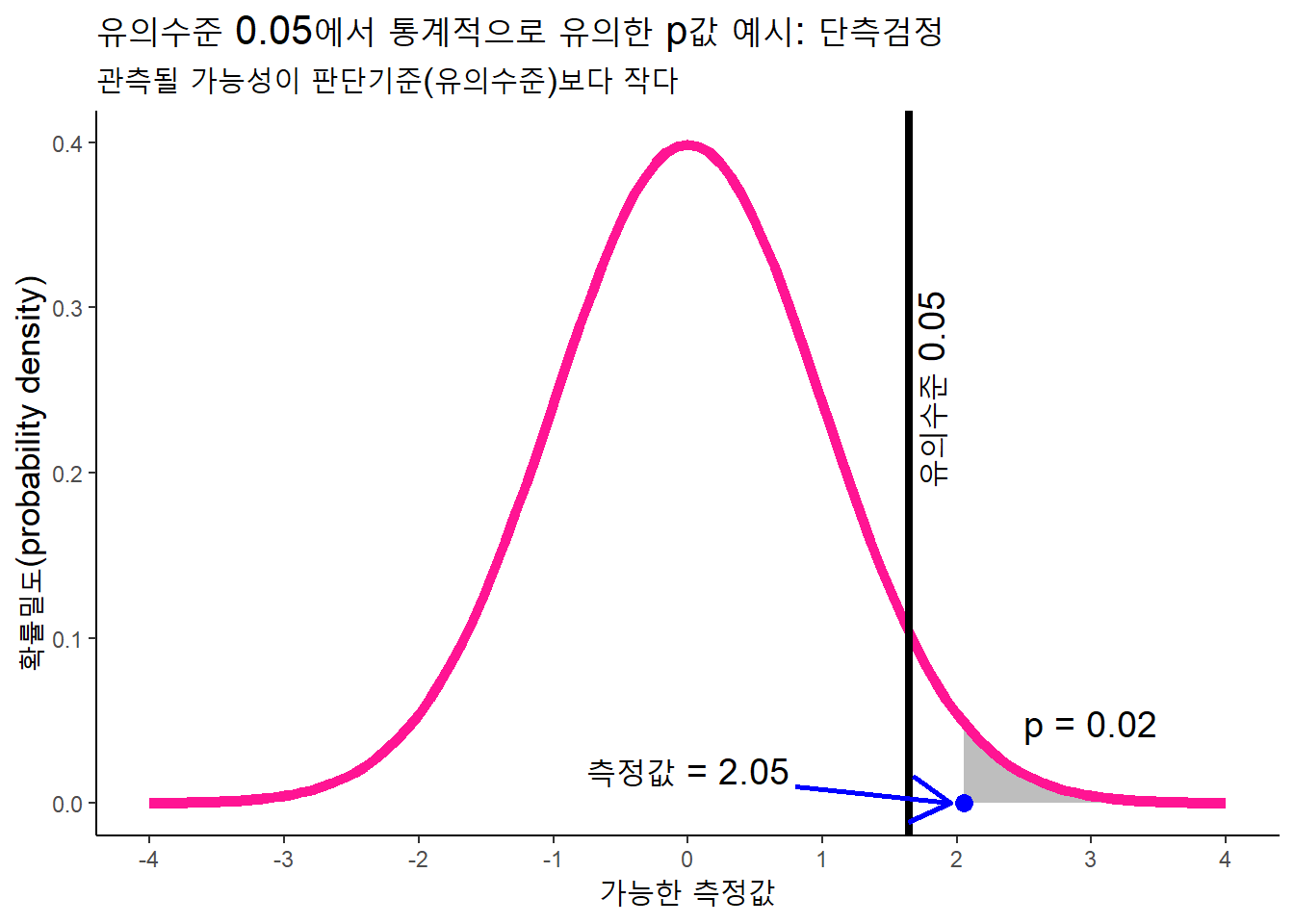
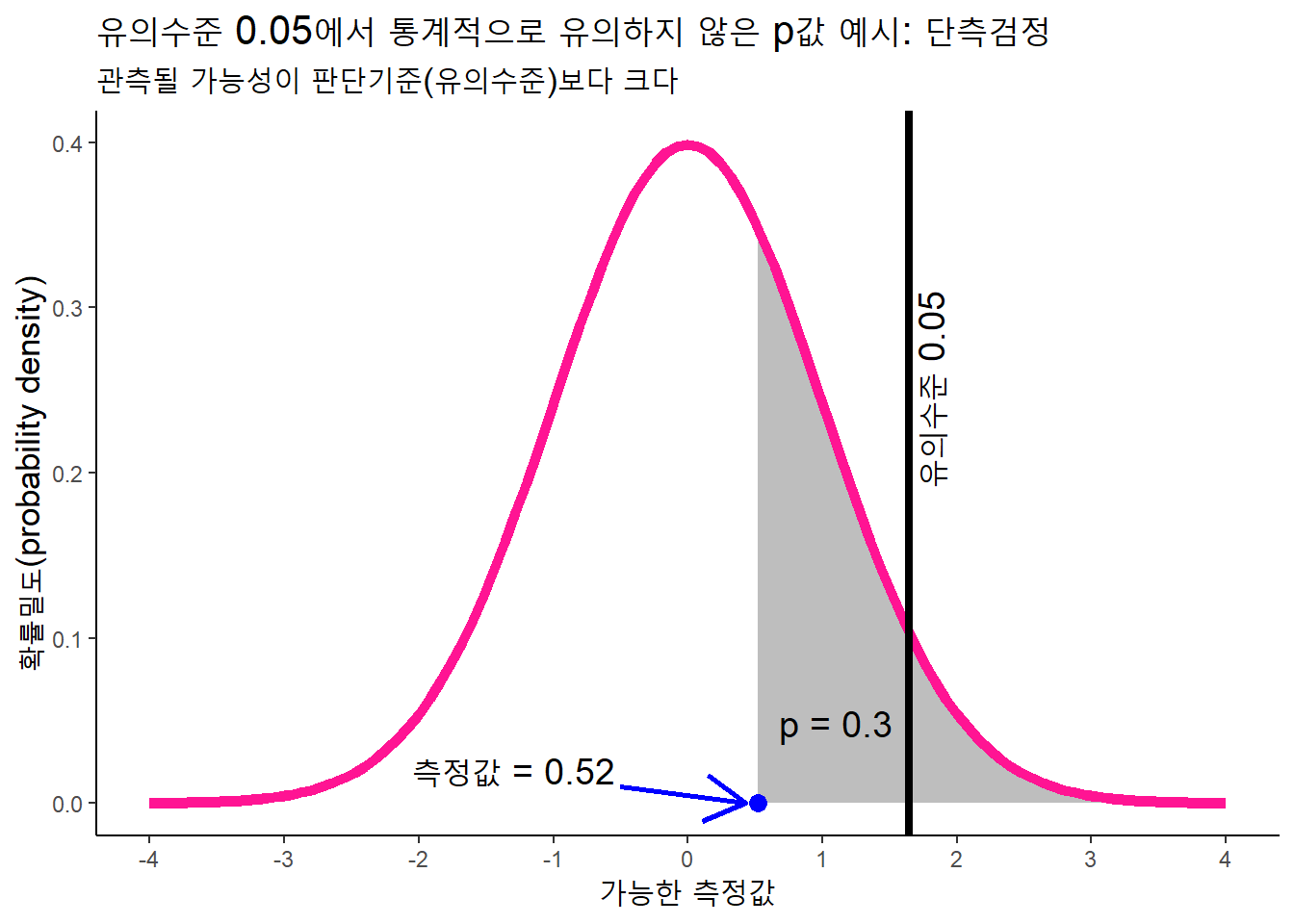
다만, \(p\)값을 사용할때 맥락을 고려해야 한다. \(p\)값 0.05라는 것은 우연일 가능성이 정말로 작은 것인지 혹은 큰 것인지는 맥락에 따라 다르기 때문이다. 예를 들어, 표본이 40만명이나 되는데, \(p\)값이 0.05미만이므로 “통계적으로 유의하다”고 주장하면 안된다. 통계적으로 유의하다는 것이 실제적으로도 늘 유의미한 것은 아니다.

새로운 관계를 발견하기 위한 탐색적인 연구라면 \(p\)값 0.05는 유의하게 작다고 할수 있으나, 인구 전체를 대상으로 실행할 정책에 적용하기 위한 근거로서는 유의하게 작다고 할 수 없다. 따라서 학계에서 관행적으로 사용하는 유의성 판단 기준 0.05를 맥락없이 남용해서는 안된다.

5.3 인과모형

상관성은 말 그대로 상호 관련성이다. 상호관련성 착시일뿐 관계의 실재는 아니다. 관계의 실재를 파악하기 위해서 우리는 일련의 인식의 과정을 거친다. 여기서 우리가 채택한 인식방법은 과학이다.

과학은 여러 인식의 방법 중 하나로서 체계적인 논리와 체계적인 경험(수집+측정)을 통해 세상을 이해하는 방법이다. 체계적인 논리를 구성하기 위해서는 이론이 필요하다. 이론은 인과모형을 통해 구성할 수 있다. 인과모형에는 원인과 결과가 있다.

두 변수(\(X\), \(Y\)) 사이에 상관성이 관측됐을 때, 그 상관성은 착시이므로, \(X\)와 \(Y\) 사이의 진정한 관계가 무엇인지 파악해야 한다. 3가지 가능성이 있다(Pearl and Mackenzie 2018).

1. 허위관계: 제3변수의 작용

상관성이 관측되나, 관측된 상관성은 제3변수의 작용에 따른 착시일뿐 실제적인 연관성은 없는 관계다. 허위 상관관계(spurious correlation)라고도 한다. 관측된 상관관계가 실제가 아닌 허위이기 때문이다. 허위관계를 만드는 제3변수는 혼란변수(confounder)와 충돌변수(collider) 두 종류가 있다.

  • 혼란변수: \(X\) ← \(C\) → \(Y\)

    • 독립변수와 종속변수에 동시에 영향을 주는 제3의 변수. 혼동변수 또는 교란변수라고도 한다. 예를 들어, 아동의 발크기(\(X\))와 계산능력(\(Y\))의 상관관계는 나이라는 혼란변수(\(C\))가 발크기(\(X\))를 늘리고, 동시에 계산능력(\(Y\))을 높게 하기 때문에 나타난 착시다.

  • 충돌변수: \(X\) → \(C\) ← \(Y\)

    • 혼란변수와 비슷해 보이나 논리적인 관계는 반대인 경우다. 독립변수와 종속변수로부터 동시에 영향을 받는 제3의 변수. 예를 들어, 연기력(\(X\))과 미모(\(Y\))의 관계를 보자. 연기력이 뛰어날수록 미모 수준이 높아지는 상관성은 충돌변수 연예명성(\(C\))에 의한 허위관계다. 연기력이 뛰어나서 연예명성이 높아진이고, 미모가 훌륭해 연예명성이 높아졌기 때문에 나타난 상관성의 착시다.

2. 역인과관계: \(X\) ← \(Y\)

결과라고 여겼던 것이 실은 원인인 경우다. 폭력미디어의 이용(\(X\))과 공격성향(\(Y\)) 사이에 상관성이 나타났을 때, 폭력미디어를 이용했기에 공격성향이 증가했을 가능성이 있지만, 동시에 공격성향이 높기 때문에 폭력미디어를 선택했을 가능성도 있다.

역인과성을 배제하기 위해서는 시간적으로 우선하는 변수가 무엇인지 고려해야 한다. 공격성향이 미디어 이용 후에 증가했는지, 혹은 미디어이용 전부터 공격성향이 높았는지 분석함으로써 무엇이 원인이고 무엇이 결과인지 판단 가능하다.

3. 인과관계: \(X\) → \(Y\)

인과관계가 성립하기 위해서는 위의 두 가능성(허위관계, 역인과관계)를 배제할 수 있어야 한다. 인과관계는 기제(mechanism)가 제시돼야 한다. 기제 역할을 하는 변수를 매개변수(mediator)라고 한다 (\(X\) → \(M\) → \(Y\)). 독립변수가 매개변수에 영향을 주고, 매개변수가 그 영향을 종속변수에 전달하는 관계다. 예를 들어, 드라마이용(\(X\))이 공감(\(M\))을 향상시키고, 향상된 공감(\(M\))이 친사회성(\(Y\))을 증가시킨다면, 드라마이용과 친사회성 사이의 기제는 공감(매개변수)이 된다.

ggdag

ggdag은 DAG(유향 비순환 그래프: Directed Acyclic Gragh)을 구성하는 R패키지다. DAG은 꼭지점(node, vertex)들 사이의 순환이 없는 방향성있는 그래프다. 꼭지점과 꼭지점은 간선(edge)으로 연결한다. ggplot2패키지와 함께 사용해 인과모형을 구성하는데 유용하다.

발크기(size)과 계산능력(competence) 사이의 상관성을 인과관계라고 간주하고, 이 둘의 관계를 다음과 같이 표현할 그릴 수 있다.

library(ggdag)
set.seed(37)
dagify(competence ~ size) %>% ggdag()

5.3.1 허위관계

상관성이 관측되나, 관측된 상관성은 제3변수의 작용에 따른 착시일뿐 실제적인 연관성은 없는 관계다. 아동의 발 크기와 계산 능력 사이의 상관성은 나이(age)가 혼란변수로 발크기(size)와 계산능력(competence)에 동시에 영향을 미치기 때문이다. age를 혼란변수로 투입해 관계도를 그려 보자. 도표의 배경도 단순화하자. 파이핑이 아니라 +로 레이어를 더한 것에 주의.

set.seed(37)
dagify(
  competence ~ age,
  size ~ age
) %>% ggdag() + theme_dag()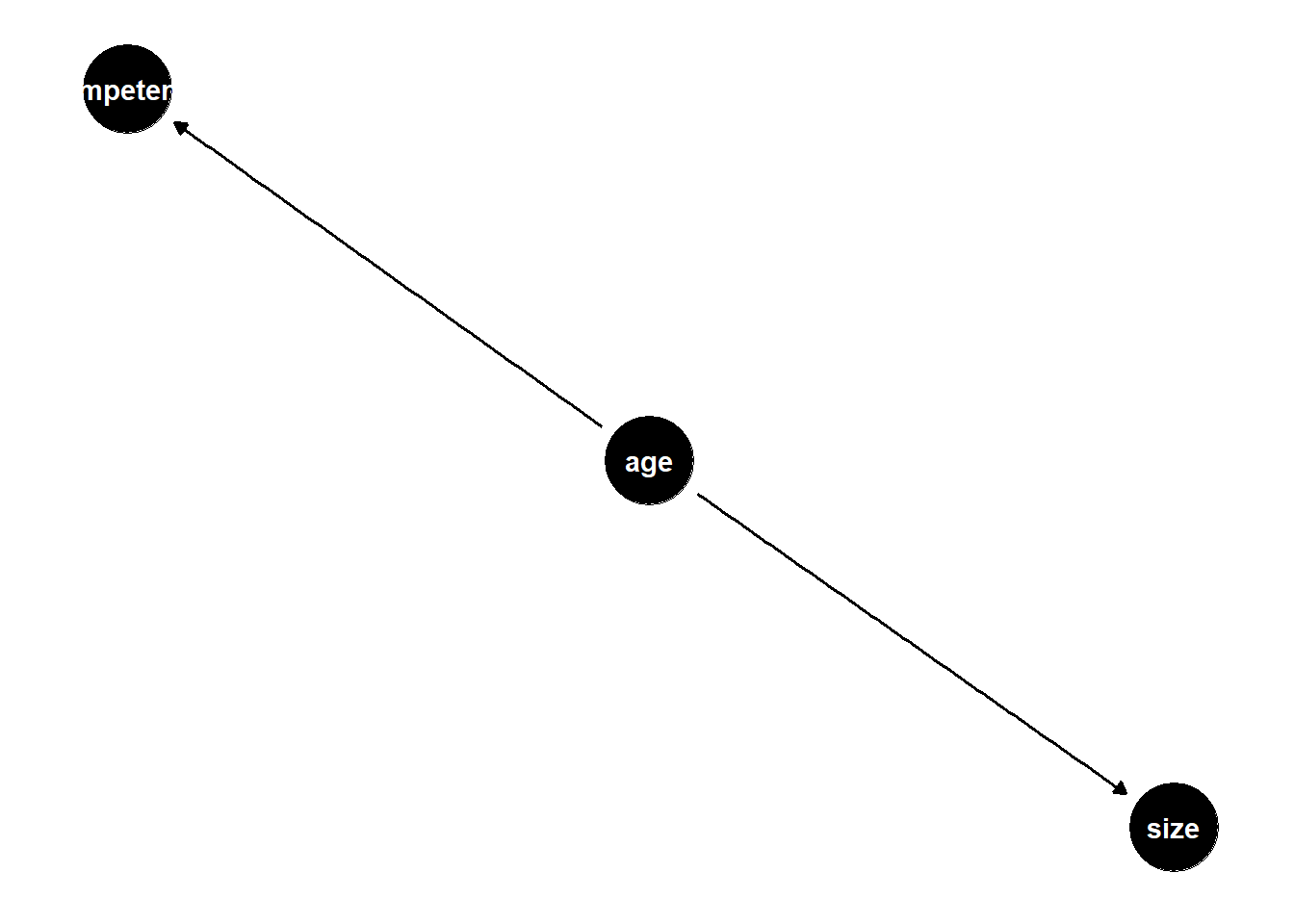

size와 competence 사이의 관련성을 양쪽 화살표로 표시하려면 ~~을 이용한다.

set.seed(8)
dagify(
  competence ~ age,
  size ~ age,
  size ~~ competence
) %>% ggdag() + theme_dag()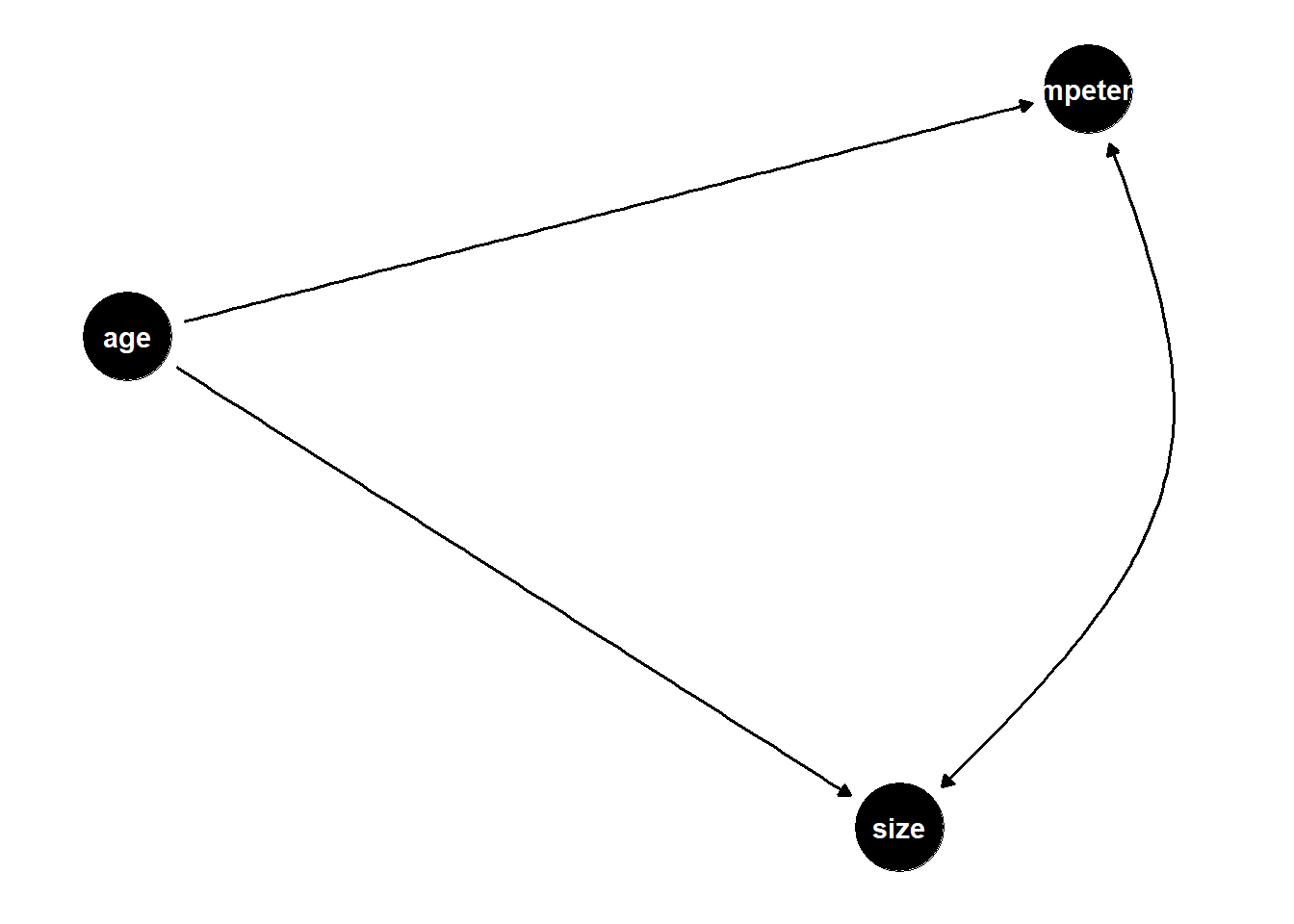

제3변수를 조정한 관계를 표시하려면 ggdag_adjust()함수를 이용한다.

set.seed(8)
dagify(
  competence ~ age,
  size ~ age,
  competence ~~ size
) %>% ggdag_adjust(var = "age")

ggdag 관계도에서 노드와 글자의 색을 바꾸려면, tidy_dagitty()로 데이터프레임으로 만들어 ggplot2를 추가하면 된다.

set.seed(37)
dagify(
  competence ~ age,
  size ~ age
) %>% tidy_dagitty()
## # A DAG with 3 nodes and 2 edges
## #
## # A tibble: 4 x 8
##   name           x     y direction to          xend  yend circular
##   <chr>      <dbl> <dbl> <fct>     <chr>      <dbl> <dbl> <lgl>   
## 1 age         29.2  22.4 ->        competence  28.4  23.2 FALSE   
## 2 age         29.2  22.4 ->        size        30.0  21.6 FALSE   
## 3 competence  28.4  23.2 <NA>      <NA>        NA    NA   FALSE   
## 4 size        30.0  21.6 <NA>      <NA>        NA    NA   FALSE
set.seed(37)
dagify(
  competence ~ age,
  size ~ age
) %>% tidy_dagitty() %>% 
  mutate(color = case_when(
    name == "age" ~ "red",
    name == "size" ~ "green",
    TRUE ~ "blue")) %>% 
  ggplot(aes(
    x = x, xend = xend, y = y, yend = yend
  )) +
  geom_dag_point(aes(color = color), shape = 15) +
  geom_dag_edges() +
  geom_dag_text(color = "black") +
  labs(title = "혼란변수로 인한 허위관계") +
  guides(color = "none") + # 범례(legend) 제거
  theme_dag()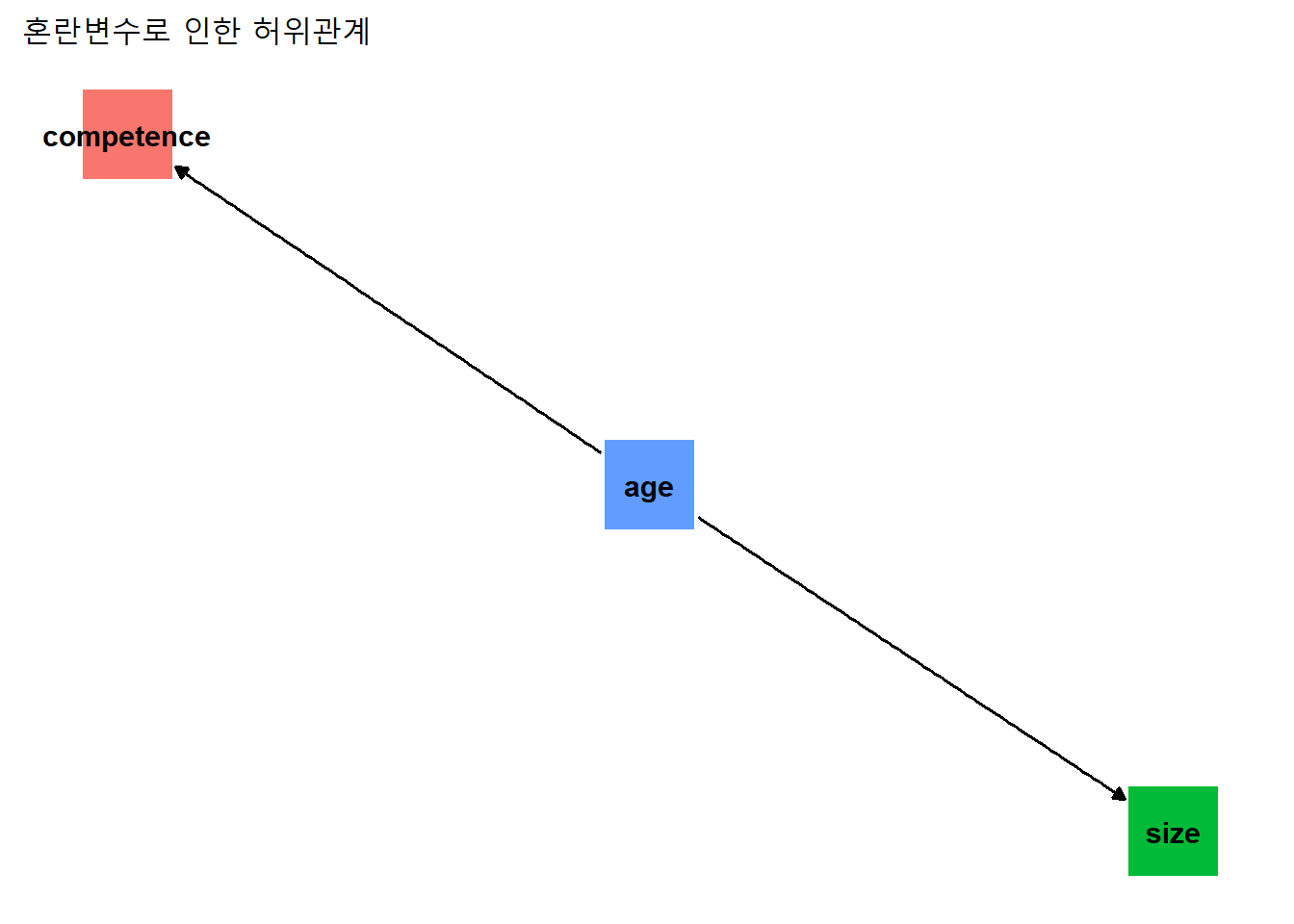

혼란변수로 인한 허위관계는 다음과 같은 관계도로 정리할 수 있다. (각 노드의 위치를 특정하려면 좌표를 미리 지정한다.)

dag_coords <-  # 좌표 데이터프레임
  data.table(
    name = c("V1", "Confounder", "V2"),
    x    = c(1, 2, 3),
    y    = c(1, 2, 1))
dagify(
  V1 ~ Confounder,
  V2 ~ Confounder,
  coords = dag_coords   # 좌표 지정
) %>% tidy_dagitty() %>% 
  ggplot(aes(
    x = x, xend = xend, y = y, yend = yend
  )) + xlim(0.7, 3.3) + ylim(0.7, 2.3)+
  geom_dag_point(color = "deep pink", alpha = .2, 
                 size = 15, shape = 15) +
  geom_dag_edges(edge_color = "deep pink") +
  geom_dag_text(color = "black") +
  labs(title = "혼란변수로 인한 허위관계") +
  theme_dag()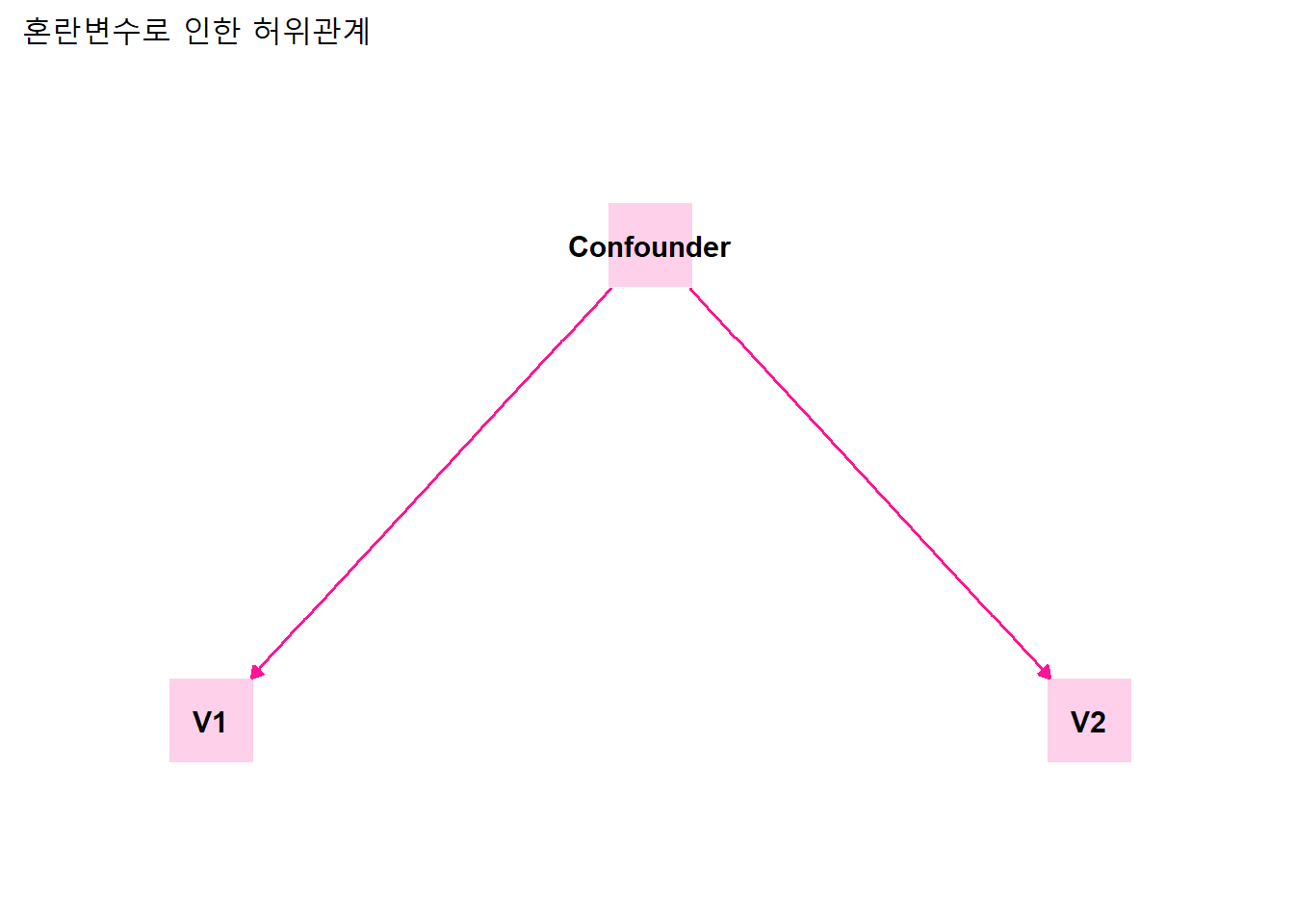

5.3.1.1 허위관계 사례

age가 혼란변수로서 competence의 원인이고, age가 size의 원인으로 작용하는 데이터셋을 만들어보자. 고학년과 저학년 집단 내에서는 각각 발크기과 계산능력 사이의 상관성이 없는데, 고학년 아동이 저학년 아동보다 발이 크고, 계산능력도 좋도록 자료를 구성한다.

회귀선을 모든 집단을 포괄하는 경우와, 각 집단을 구분하는 경우로 나눠 설정하도록 시각화 사용자함수 viz_f()를 만든다.

N <- 1000
set.seed(37)
ivg1 <- rnorm(N, 230, 50)
set.seed(41)
ivg2 <- rnorm(N, 140, 50)
set.seed(43)
e <- rnorm(N, 30, 4)
df <- data.table( # 고학년 데이터프레임
  x = ivg1,  
  y = 50 + 0.0001*ivg1 + e,  # 무관계이므로 기울기 최소화
  z = rep("고학년", N)) %>% 
  bind_rows.(data.table( # 저학년 데이터프레임
  x = ivg2, 
  y = 30 + 0.0001*ivg2 + e,  # 무관계이므로 기울기 최소화
  z = rep("저학년", N))) 

viz_f <- function(df, xlab, ylab, zlab){
df %>% ggplot() + 
  geom_point(aes(x, y), alpha = 0.1) +           
  # 통제변수 투입 전
  geom_smooth(aes(x, y), size = 3,
              method = lm, se = F) +
  # 통제변수 투입 후
  geom_smooth(aes(x, y, color = z), size = 4,
              method = lm, se = F) +
  labs(
    title = str_glue("{zlab}별 {xlab}와 {ylab}의 관계"),
    x = str_glue("{xlab}"), 
    y = str_glue("{ylab}"), 
    color = str_glue("{zlab}"),
    ) + theme(plot.title = element_text(size = 15)) 
}
viz_f(df, xlab = "size", ylab = "competence", zlab = "age")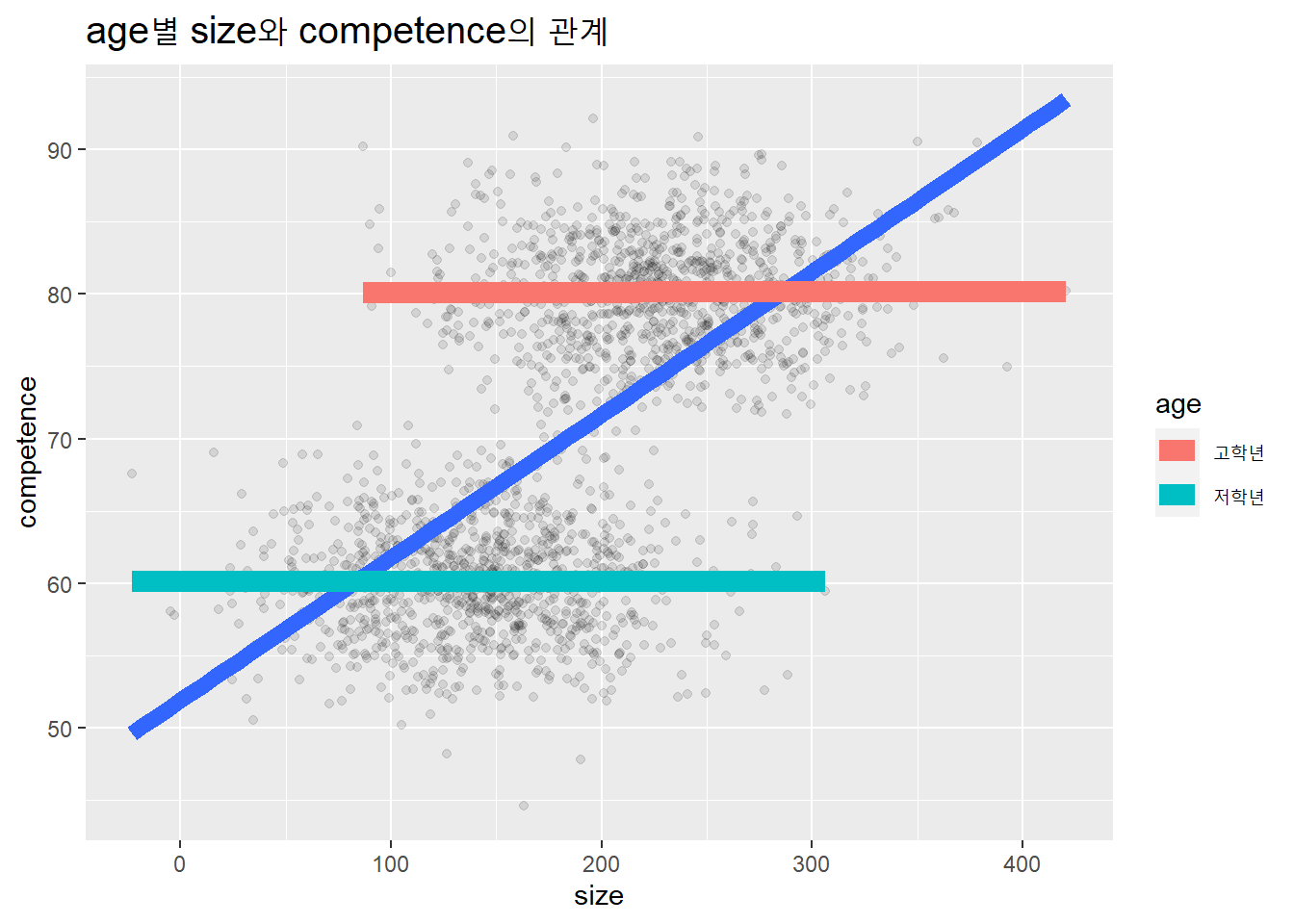

회귀모형으로 혼란변수 투입전후를 비교해보자. 먼저 회귀모형 2개를 구성한다.

names(df) <- c("size", "competence", "age")
y <- 2
x1 <- 1       # competence ~ size
xx <- c(1,3)  # competence ~ size + age
mod_two(df, y, x1, xx) -> model
data.frame(Formulas = model) %>% gt()
Formulas
competence ~ size
competence ~ size + age

두개 모형에 대해 회귀분석을 수행한다. 통계적 유의성 \(p\)값도 함께 계산한다. \(p\)값은 broom패키지의 tidy()함수로 산출 데이터프레임의 p.value열에 있다. 열의 수가 많아지므로 표준화계수는 제외하고 출력한다.

df %>% lm(model[1], .) %>% tidy()
## # A tibble: 2 x 5
##   term        estimate std.error statistic   p.value
##   <chr>          <dbl>     <dbl>     <dbl>     <dbl>
## 1 (Intercept)  51.9      0.555        93.5 0        
## 2 size          0.0988   0.00283      35.0 2.87e-209
nn <- length(xx) + 1 # IV행 + 절편행 개수
### 회귀분석 사용자함수
reg_f <- function(nn, model){  
  output <- list()
  for (i in seq_along(model)) {
    fit <- df %>% lm(model[i], .)
    # 변수명, 회귀계수, 표준오차 데이터프레임
    op <- tidy(fit)[1:nn, -4] %>% # statitic열 빼고 선택
      # 결정계수 데이터프레임
      bind_rows.(data.frame(
        term = c("결정계수",
                 "수정결정계수"),
        estimate = NA,
        std.error = c(summary(fit)$r.squared,
                     summary(fit)$adj.r.squared),
        p.value = NA
      ))
    output <- list(output, op)
  }
  return(output)
}
(reg_f(nn, model) -> fit)
## [[1]]
## [[1]][[1]]
## list()
## 
## [[1]][[2]]
## # A tidytable: 5 x 4
##   term         estimate std.error    p.value
##   <chr>           <dbl>     <dbl>      <dbl>
## 1 (Intercept)   51.9      0.555    0        
## 2 size           0.0988   0.00283  2.87e-209
## 3 <NA>          NA       NA       NA        
## 4 결정계수      NA        0.379   NA        
## 5 수정결정계수  NA        0.379   NA        
## 
## 
## [[2]]
## # A tidytable: 5 x 4
##   term            estimate std.error p.value
##   <chr>              <dbl>     <dbl>   <dbl>
## 1 (Intercept)   80.1         0.423     0    
## 2 size           0.0000360   0.00176   0.984
## 3 age저학년    -20.0         0.237     0    
## 4 결정계수      NA           0.864    NA    
## 5 수정결정계수  NA           0.864    NA

각 모형의 계산결과를 하나의 데이터프레임으로 결합하고, 표로 정리한다.

### 모형 2개 결합해 표로 정리
tbl_two <- function(df, fit){
  fit[[1]][[2]] %>%
    bind_cols.(fit[[2]]) %>%
    select.(term = term...5, # 모형2 변수명
            estimate...2:p.value...8) %>%
    gt() %>%
    tab_header(str_glue("{names(df)[y]}에 대한 회귀분석결과")) %>%
    fmt_number(-1, decimals = 2) %>%
    # p값은 소숫점 3자리
    fmt_number(starts_with("p.value"), decimals = 3) %>% 
    fmt_missing(-1, missing_text = html("<br>")) %>%
    cols_label(
      term = md("IV"),
      estimate...2 = md("_B_"),
      std.error...3 = md("_SE_"),
      p.value...4 = md("_p_"),
      estimate...6 = md("_B_"),
      std.error...7 = md("_SE_"),
      p.value...8 = md("_p_")
    ) %>%
    tab_spanner(
      label = "Model 1",
      columns = estimate...2:p.value...4) %>%
    tab_spanner(
      label = "Model 2",
      columns = estimate...6:p.value...8) %>%
    text_transform(
      locations = 
        cells_body(
          columns = term,
          rows = term == "결정계수"),
        fn = function(x) {
          html(
            "<p align='center'><em>R<sup>2</sup></em></p>")
        }) %>% 
    text_transform(
      locations = 
        cells_body(
          columns = term,
          rows = term == "수정결정계수"),
        fn = function(x) {
          html(
            "<p align='center'><em>R<sup>2</sup><sub>adj</sub></em></p>")
        }) %>% 
    tab_footnote(
      footnote = str_glue("N = {nrow(df)}"),
      locations = cells_title()
    )
}
tbl_two(df, fit)
competence에 대한 회귀분석결과1
IV Model 1 Model 2
B SE p B SE p
(Intercept) 51.88 0.56 0.000 80.11 0.42 0.000
size 0.10 0.00 0.000 0.00 0.00 0.984
age저학년


−20.01 0.24 0.000

R2
0.38

0.86

R2adj
0.38

0.86
1 N = 2000

size의 competence에 대한 회귀계수가 age를 통제하지 않았을때는 0.1로 통계적으로 유의하다(\(p\) < 0.001), age를 통제하면 계수가 0로 감소하며 통계적 유의성도 사라진다(\(p\) < 0.984).

반면, age를 독립변수로 투입하고 size를 통제변수로 투입하면, age를 단독 독립변수로 투입한 모형1에서 competence에 대한 회귀계수는 size를 통제변수로 추가한 모형2에서는 회귀계수가 거의 변화가 없다.

names(df) <- c("size", "competence", "age")
y <- 2
x1 <- 3       # competence ~ age
xx <- c(3,1)  # competence ~ age + size
nn <- length(xx) + 1
mod_two(df, y, x1, xx) -> model
data.frame(Formulas = model) %>% gt()
Formulas
competence ~ age
competence ~ age + size
 
model %>% 
  reg_f(nn, .) %>% 
  tbl_two(df, .)
competence에 대한 회귀분석결과1
IV Model 1 Model 2
B SE p B SE p
(Intercept) 80.12 0.13 0.000 80.11 0.42 0.000
age저학년 −20.01 0.18 0.000 −20.01 0.24 0.000
size


0.00 0.00 0.984

R2
0.86

0.86

R2adj
0.86

0.86
1 N = 2000

5.3.2 충돌관계

충돌관계는 관계처럼 두 변수가 충돌변수에 대해 동시에 원인으로 작용하기 때문에 나타나는 일종의 허위관계다.

dag_coords <-  # 좌표 데이터프레임
  data.table(
    name = c("V1", "Collider", "V2"),
    x    = c(1, 2, 3),
    y    = c(1, 2, 1))
dagify(
  Collider ~ V1,
  Collider ~ V2,
  coords = dag_coords   # 좌표 지정
) %>% tidy_dagitty() %>% 
  ggplot(aes(
    x = x, xend = xend, y = y, yend = yend
  )) + xlim(0.7, 3.3) + ylim(0.7, 2.3) +
  geom_dag_point(color = "blue", alpha = .2, 
                 size = 15, shape = 15) +
  geom_dag_edges(edge_color = "blue") +
  geom_dag_text(color = "black") +
  labs(title = "충돌변수로 인한 허위관계") +
  theme_dag()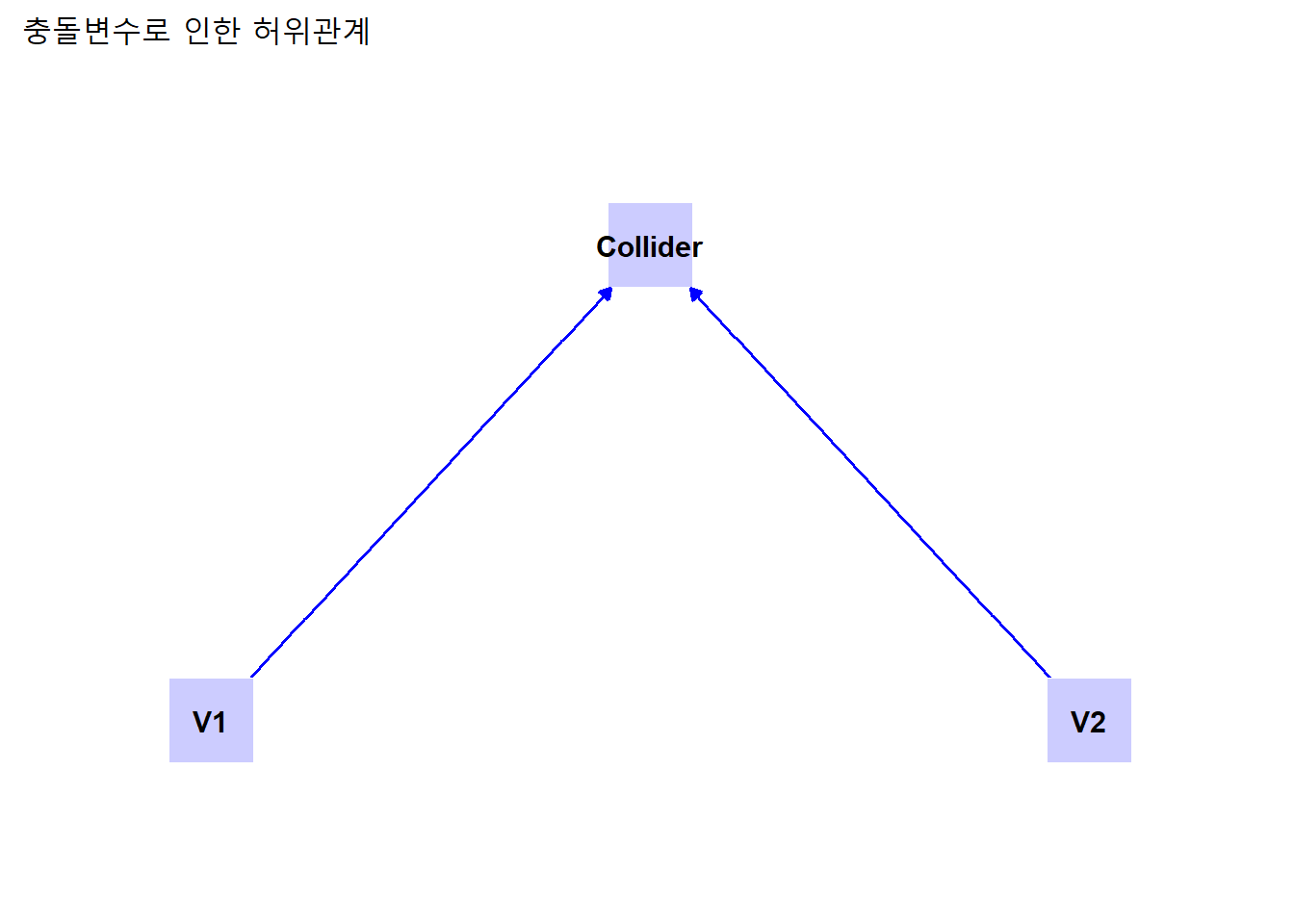

예를 들어, 연예명성(Celeb), 연기력(Telent), 미모(Beauty)의 관계에서 연기력과 미모가 동시에 연예명성에 대해 원인으로 작용해 연기력과 미모 사이에 상관성이 나타나는 경우다.

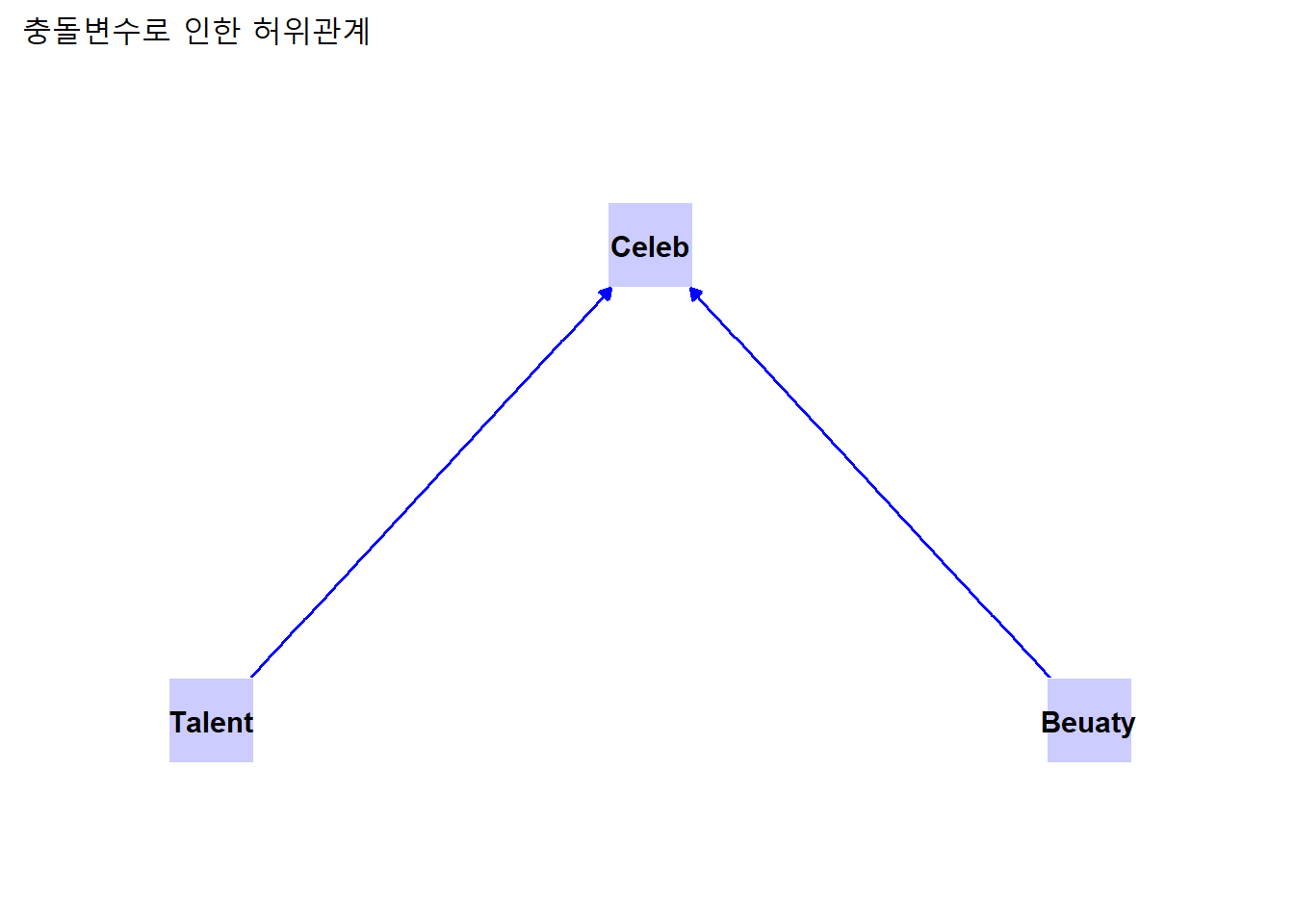
5.3.3 합산모형

혼란변수로 인한 허위관계 여부를 판단하기 위해서는 혼란변수를 통제해 두 변수 사이의 상관성이 허위임을 밝힐 수 있으나, 충돌관계에서는 충돌변수를 통제해서는 안된다. 충돌관계는 종속변수를 잘못 설정한 경우에 해당하기 때문이다.

연예명성 사례의 경우, 연기력과 미모가 독립변수와 종속변수 혹은 종속변수와 독립변수의 관계라기 보다, 연기력과 미모가 각각 독립변수로서 종속변수인 연예명성에 영향을 미치는 관계로 파악하는 것이 타당하다.

이처럼 두개의 원인이 서로 독립적으로 합산해(additive) 종속변수를 설명하는 모형을 합산모형이라고 한다.

dag_coords <-  # 좌표 데이터프레임
  data.table(
    name = c("Talent", "Beauty", "Celeb"),
    x    = c(1, 2, 3),
    y    = c(1, 2, 1))
dagify(
  Celeb ~ Talent + Beauty,
  coords = dag_coords   # 좌표 지정
) %>% tidy_dagitty() %>% 
  ggplot(aes(
    x = x, xend = xend, y = y, yend = yend
  )) + xlim(0.7, 3.3) + ylim(0.7, 2.3) +
  geom_dag_point(color = "green", alpha = .5, 
                 size = 15, shape = 15) +
  geom_dag_edges(edge_color = "green") +
  geom_dag_text(color = "black") +
  labs(title = "두개의 원인에 의한 합산모형") +
  theme_dag()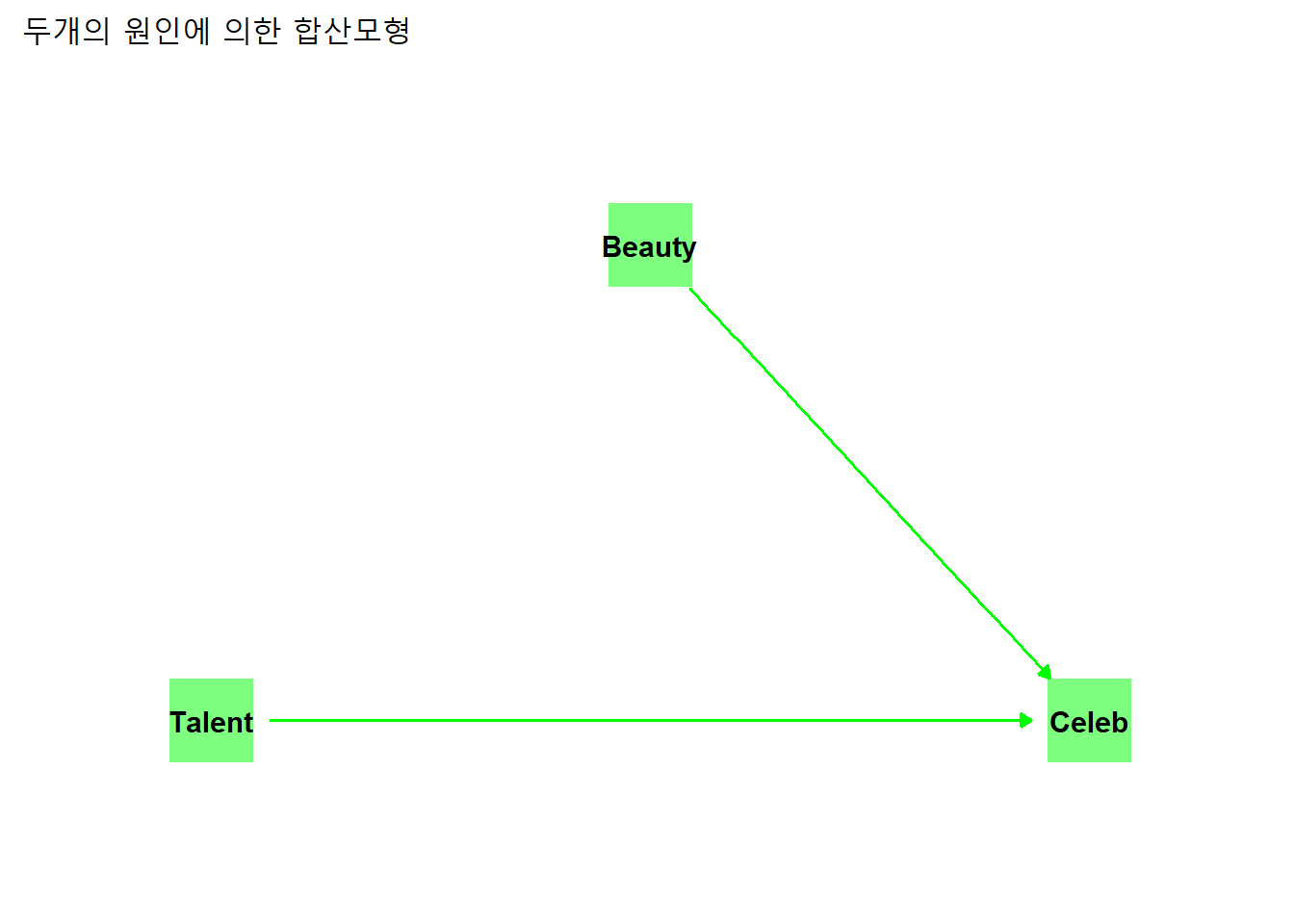

5.3.3.1 합산모형 사례

talent과 beauty가 각각 독립변수로서 종속변수 celeb에 영향을 미치는 데이터셋을 만들어 시각화하자. talent와 celeb의 기울기는 beauty의 요인(상, 하)별 구분한 집단에서의 talent와 celeb의 기울기가 동일하다.

N <- 1000
set.seed(37)
ivg1 <- rnorm(N, 300, 50)
set.seed(41)
ivg2 <- rnorm(N, 300, 50)
set.seed(43)
e <- rnorm(N, 30, 30)
df <- data.table(
  x = ivg1,  
  y = 200 + 0.7*ivg1 + e,   # 기울기 동일하게 설정
  z = rep("상", N)) %>% 
  bind_rows.(data.table(
  x = ivg2, 
  y = 50 + 0.7*ivg2 + e,    # 기울기 동일하게 설정
  z = rep("하", N))) 
viz_f(df, xlab = "talent", ylab = "celeb", zlab = "beauty")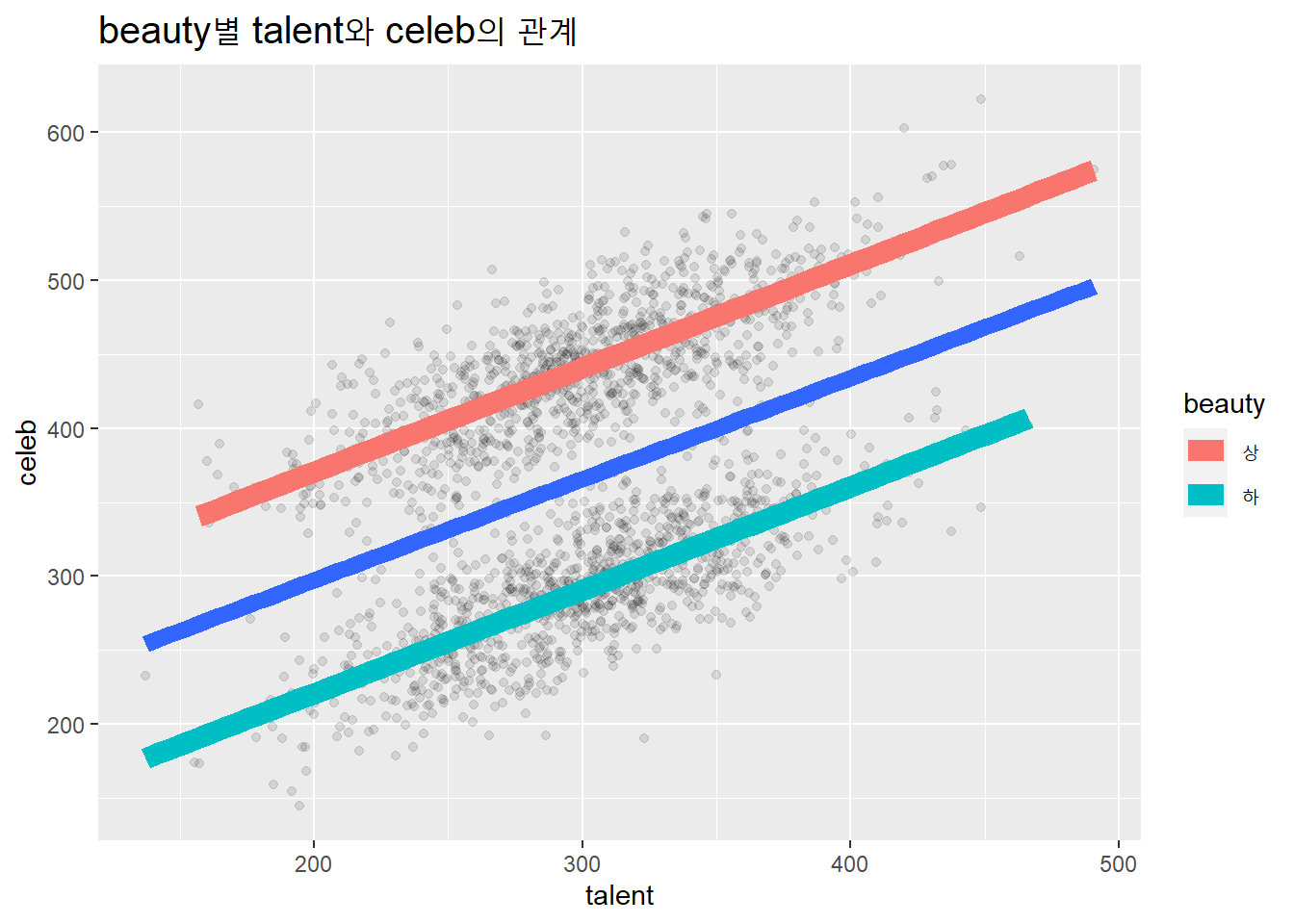

합산모형 여부를 판단하기 위해서는 각 독립변수가 서로 독립적으로 종속변수에 대한 설명력이 합산적인지 봐야 한다. 이를 위해서는 각 독립변수를 단독으로 투입한 회귀모형 2개와 두 독립변수를 함께투입한 회귀모형 등 3개의 회귀모형이 필요하다.

names(df) <- c("talent", "celeb", "beauty")
y <- 2
x1 <- 1          # celeb ~ talent
x2 <- 3          # celeb ~ beauty
xx <- c(x1, x2)  # celeb ~ talent + beauty
### 회귀모형 3종 생성
mod_three <- function(df, y, x1, x2, xx) {
## 변수 및 회귀모형
  # 변수
  dv <- names(df)[y]
  iv1 <- names(df)[x1]
  iv2 <- names(df)[x2]
  iv3 <- names(df)[xx]
  # 모형1 회귀식
  fml_mdl1 <- iv1 %>%
    paste0(., collapse = " + ") %>%
    paste0(dv, " ~ ", .)
  # 모형2 회귀식
  fml_mdl2 <- iv2 %>%
    paste0(., collapse = " + ") %>%
    paste0(dv, " ~ ", .)
  # 모형3 회귀식
  fml_mdl3 <- iv3 %>%
    paste0(., collapse = " + ") %>%
    paste0(dv, " ~ ", .)
## 회귀분석 + 데이터프레임결합
  model <- c(fml_mdl1, fml_mdl2, fml_mdl3)
  return(model)
}
mod_three(df, y, x1, x2, xx) -> model
data.frame(Fomulas = model) %>% gt()
Fomulas
celeb ~ talent
celeb ~ beauty
celeb ~ talent + beauty

talent와 beauty가 각각 독립적으로 celeb에 영향을 미치는 단순회귀 모형2개 및 telent와 beauty를 함께 독립변수로 투입한 다중회귀모형을 만들어 회귀계수를 계산하자.

nn <- length(xx) + 1
model %>% 
  reg_f(nn, .) -> fit
fit
## [[1]]
## [[1]][[1]]
## [[1]][[1]][[1]]
## list()
## 
## [[1]][[1]][[2]]
## # A tidytable: 5 x 4
##   term         estimate std.error   p.value
##   <chr>           <dbl>     <dbl>     <dbl>
## 1 (Intercept)   161.      10.9     1.06e-46
## 2 talent          0.684    0.0359  1.94e-74
## 3 <NA>           NA       NA      NA       
## 4 결정계수       NA        0.154  NA       
## 5 수정결정계수   NA        0.153  NA       
## 
## 
## [[1]][[2]]
## # A tidytable: 5 x 4
##   term         estimate std.error p.value
##   <chr>           <dbl>     <dbl>   <dbl>
## 1 (Intercept)      440.     1.46        0
## 2 beauty하        -149.     2.06        0
## 3 <NA>              NA     NA          NA
## 4 결정계수          NA      0.724      NA
## 5 수정결정계수      NA      0.724      NA
## 
## 
## [[2]]
## # A tidytable: 5 x 4
##   term         estimate std.error p.value
##   <chr>           <dbl>     <dbl>   <dbl>
## 1 (Intercept)   231.       4.07         0
## 2 talent          0.700    0.0132       0
## 3 beauty하     -150.       1.33         0
## 4 결정계수       NA        0.885       NA
## 5 수정결정계수   NA        0.885       NA

모형 3개를 결합하기 위해서는 두번째 모형(celeb ~ beauty)에서 독립변수가 제시되는 순서가 바뀌어야 한다.

fit[[1]][[2]][1,] %>%  # 절편행
  bind_rows.(fit[[1]][[2]][3,]) %>%  # NA행
  bind_rows.(fit[[1]][[2]][2,]) %>%  # 독립변수 행
  bind_rows.(fit[[1]][[2]][4:5,]) -> fit[[1]][[2]]
fit[[1]][[2]]
## # A tidytable: 5 x 4
##   term         estimate std.error p.value
##   <chr>           <dbl>     <dbl>   <dbl>
## 1 (Intercept)      440.     1.46        0
## 2 <NA>              NA     NA          NA
## 3 beauty하        -149.     2.06        0
## 4 결정계수          NA      0.724      NA
## 5 수정결정계수      NA      0.724      NA

사용자함수 tbl_three()를 만들어 회귀분석결과 3개를 결합해 표로 정리하자.

## 모형3개 결합해 표로 정리
tbl_three <- function(df, fit){
  fit[[1]][[1]][[2]] %>%
    bind_cols.(fit[[1]][[2]]) %>%
    bind_cols.(fit[[2]]) %>%
    select.(term = term...9, # 모형3 변수명
            estimate...2:p.value...4, 
            estimate...6:p.value...8,
            estimate...10:p.value...12
            ) %>%
    gt() %>%
    tab_header(str_glue("{names(df)[y]}에 대한 회귀분석결과")) %>%
    fmt_number(-1, decimals = 2) %>%
    fmt_number(starts_with("p.value"), decimals = 3) %>%
    fmt_missing(-1, missing_text = html("<br>")) %>%
    cols_label(
      term = md("IV"),
      estimate...2 = md("_B_"),
      std.error...3 = md("_SE_"),
      p.value...4 = md("_p_"),
      estimate...6 = md("_B_"),
      std.error...7 = md("_SE_"),
      p.value...8 = md("_p_"),
      estimate...10 = md("_B_"),
      std.error...11 = md("_SE_"),
      p.value...12 = md("_p_")
    ) %>%
    tab_spanner(
      label = str_glue("Model 1"),
      columns = estimate...2:p.value...4) %>%
    tab_spanner(
      label = str_glue("Model 2"),
      columns = estimate...6:p.value...8) %>%
    tab_spanner(
      label = str_glue("Model 3"),
      columns = estimate...10:p.value...12) %>%
    text_transform(
      locations = 
        cells_body(
          columns = term,
          rows = term == "결정계수"),
      fn = function(x) {html(
          "<p align='center'><em>R<sup>2</sup></em></p>")
        }) %>% 
    text_transform(
      locations = 
        cells_body(
          columns = term,
          rows = term == "수정결정계수"),
      fn = function(x) {html(
          "<p align='center'><em>R<sup>2</sup><sub>adj</sub></em></p>")
        }) %>% 
    tab_footnote(
      footnote = str_glue("N = {nrow(df)}"),
      locations = cells_title()
    )
}
tbl_three(df, fit)
celeb에 대한 회귀분석결과1
IV Model 1 Model 2 Model 3
B SE p B SE p B SE p
(Intercept) 160.64 10.91 0.000 440.08 1.46 0.000 230.87 4.07 0.000
talent 0.68 0.04 0.000


0.70 0.01 0.000
beauty하


−149.25 2.06 0.000 −150.00 1.33 0.000

R2
0.15

0.72

0.89

R2adj
0.15

0.72

0.88
1 N = 2000

telent의 celeb에 대한 회귀계수가 모형1과 모형3에서 거의 같다. 모형2의 beauty의 celeb에 대한 회귀계수 역시 모형3에서 거의 변하지 않는다.

모형1의 결정계수와 모형2의 결정계수를 더하면 거의 모형3의 결정계수가 나온다.

이처럼 두 개의 독립변수가 종속변수에 대해 서로 독립적으로 영향을 미치기 때문에 두 독립변수의 종속변수에 대한 영향은 합산적(additive)이라고 할수 있다.

5.3.4 상호작용

두 독립변수가 서로 독립적이지 않은 경우, 독립변수의 종속변수에 대한 영향은 합산적이지 않고 곱셈적이 된다. 한 독립변수의 종속변수에 대한 영향을 다른 독립변수가 “조절”하기 때문이다. 이처럼 독립변수의 종속변수에 대한 영향을 조절하는 변수를 조절변수(moderator)라고 하며, 이러한 관계를 조절관계 혹은 상호작용관계라고 한다.

예를 들어, 독립변수와 종속변수의 관계에서 조절변수의 값이 큰 경우 독립변수의 증가가 종속변수의 증가로 이어지고, 조절변수의 값이 작은 경우 독립변수의 증가가 종속변수의 감소로 이어지거나 변화가 없는 경우가 조절관계다.

상호작용 관계는 다음과 같이 나타낼 수 있다.

dag_coords <-  # 좌표 데이터프레임
  data.table(
    name = c("IV", "Moderator", "DV", "holder"),
    x    = c(1, 2, 3, 2),
    y    = c(1, 2, 1, 0.9)
    )
dagify(
  DV ~ IV,
  holder ~ Moderator,
  coords = dag_coords   # 좌표 지정
) %>% tidy_dagitty() %>% 
  ggplot(aes(
    x = x, xend = xend, y = y, yend = yend
  )) + xlim(0.7, 3.3) + ylim(0.7, 2.3) +
  geom_dag_point(
    data = function(x) filter(x, name != "holder"),
    color = "green", alpha = .6,
                 size = 15, shape = 15) +
  geom_dag_edges(edge_color = "green") +
  geom_dag_text(
    data = function(x) filter(x, name != "holder"),
    color = "black") +
  labs(title = "조절변수로 인한 상호작용(개념모형)") +
  theme_dag()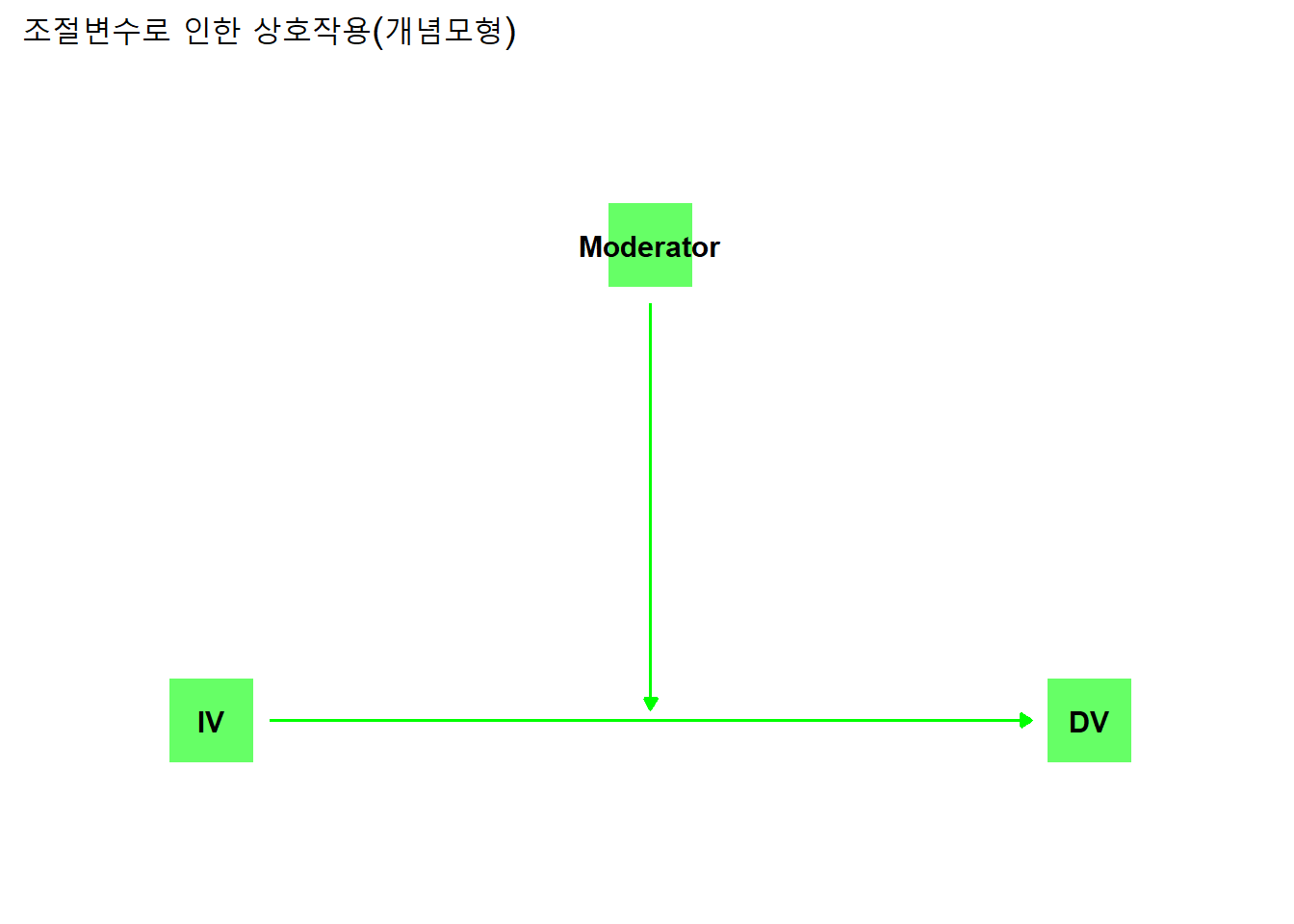

독립변수와 조절변수는 곱셈관계이기 때문에 실제 계산할 때 사용하는 모형은 다음과 같다.

dag_coords <-  # 좌표 데이터프레임
  data.table(
    name = c("IV", "Moderator", "DV", "IVxModerator"),
    x    = c(1, 2, 3, 2),
    y    = c(1, 2, 1, 1.5)
    )
dagify(
  DV ~ IV,
  DV ~ Moderator,
  DV ~ IVxModerator,
  coords = dag_coords   # 좌표 지정
) %>% tidy_dagitty() %>% 
  ggplot(aes(
    x = x, xend = xend, y = y, yend = yend
  )) + xlim(0.7, 3.3) + ylim(0.7, 2.3) +
  geom_dag_point(
    data = function(x) filter(x, name != "holder"),
    color = "green", alpha = .6,
                 size = 15, shape = 15) +
  geom_dag_edges(edge_color = "green") +
  geom_dag_text(
    data = function(x) filter(x, name != "holder"),
    color = "black") +
  labs(title = "조절변수로 인한 상호작용(계산모형)") +
  theme_dag()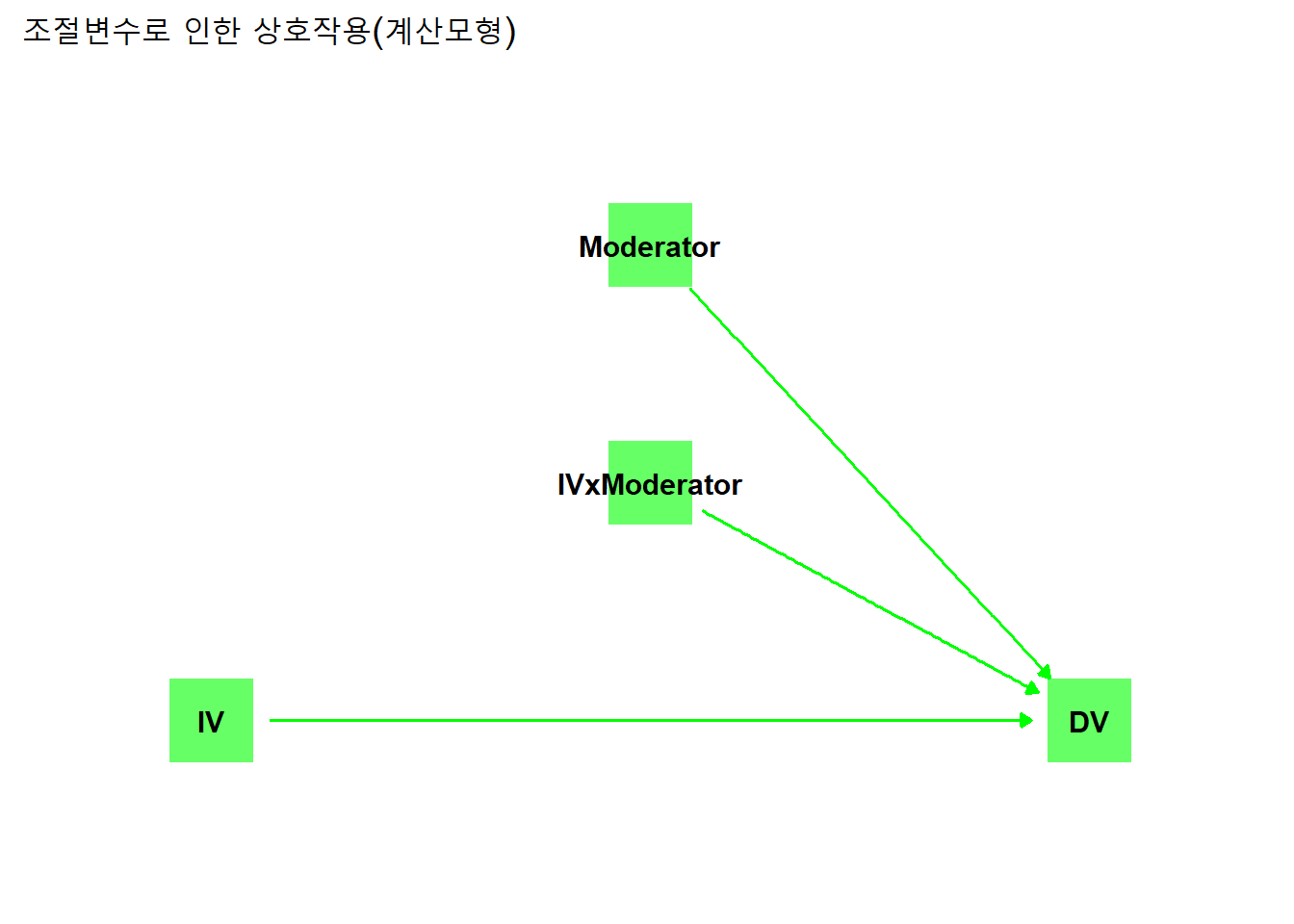

따라서 상호작용의 회귀모형은 다음과 같다. \(Z\)가 조절변수다.

\[ Y = \alpha + \beta_1X + \beta_2Z + \beta_3X*Z + \epsilon \]

5.3.4.1 상호작용 사례1

이야기이용시간(IV)과 친사회성(DV)의 관계를 예로 들어보자. 통상적으로 이야기 이용시간과 친사회성 사이에 상관성이 관측되지 않았다고 하자. 그렇다면, 이야기의 이용과 친사회성 사이의 관계는 없다고 판단해도 될까?

앞서, 허위관계는 상관성이 관측됐지만 실은 제3변수(허위변수)의 작용에 의한 착시임을 설명했다. 여기서 소개하는 상호작용관계는 그와 반대인 경우다. 상관성이 관측되지 않았지만 제3변수(조절변수)의 작용을 고려하면 연관성이 드러난다.

이야기이용과 친사회성의 관계를 조절하는 변수는 이야기의 장르다. 장르가 드라마인 경우 이야기이용시간이 늘수록 친사회성이 증가하고, 이야기 장르가 공포인 경우 이야기이용시간이 늘수록 친사회성이 감소하거나 변화가 없을수 있다.

가상의 데이터셋을 만들어 상호작용을 살펴보자.

N <- 1000
set.seed(37)
ivg1 <- rnorm(N, 300, 50)
set.seed(41)
ivg2 <- rnorm(N, 300, 50)
set.seed(43)
e <- rnorm(N, 30, 30)
df <- data.table(
  x = ivg1,  
  y = 50 + 0.5*ivg1 + e,
  z = rep("드라마", N)) %>% 
  bind_rows.(data.table(
  x = ivg2, 
  y = 200 - 0.5*ivg2 + e,   # 기울기 반대방향으로 설정
  z = rep("공포", N))) 
viz_f(df, xlab = "이야기", ylab = "친사회성", zlab = "장르")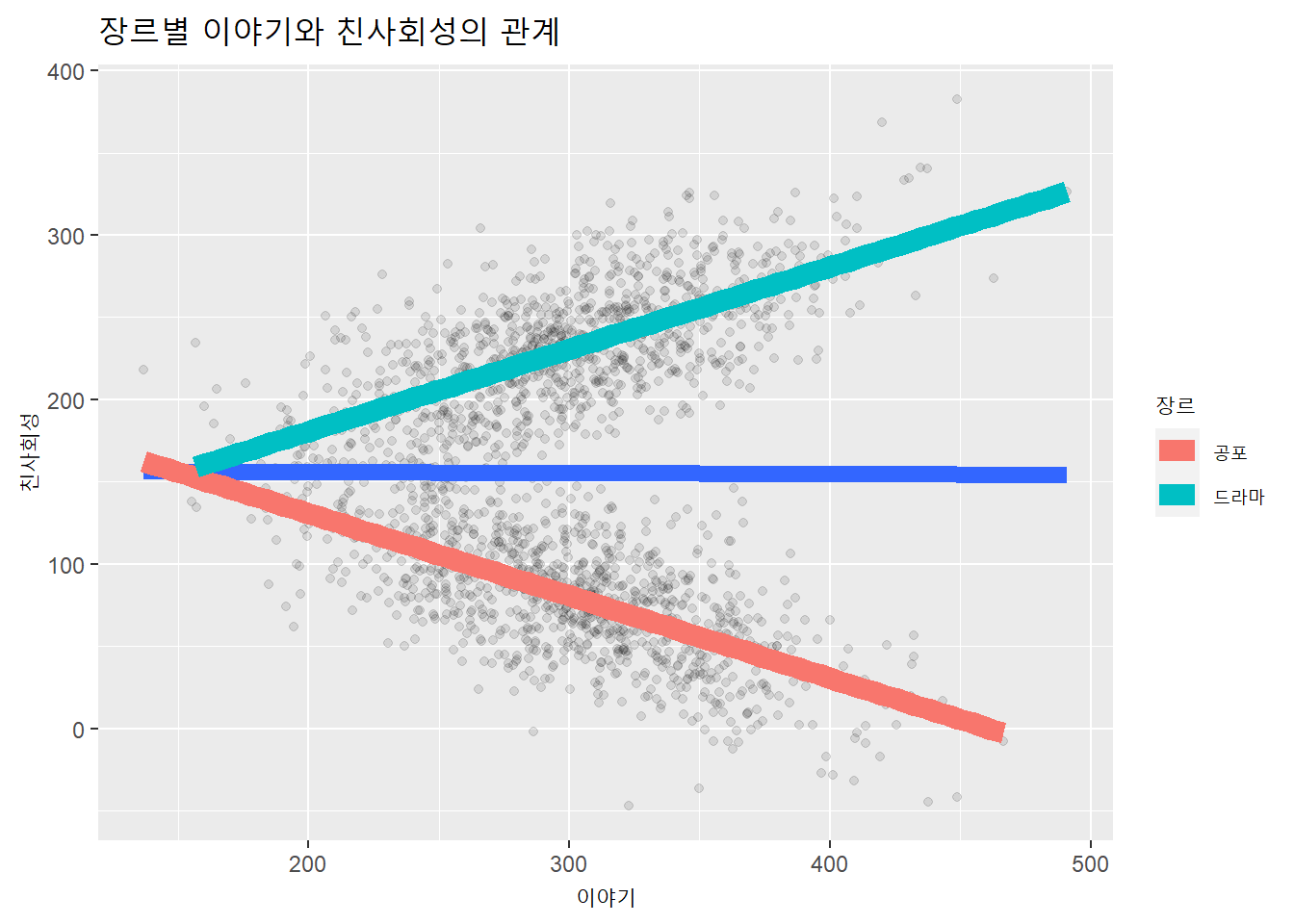

위 조절관계를 회귀모형으로 구성하면 다음과 같다.

names(df) <- c("이야기", "친사회성", "장르")
lm(친사회성 ~ 이야기 + 장르 + 이야기*장르, df) %>% extract_eq()

\[ \operatorname{친사회성} = \alpha + \beta_{1}(\operatorname{이야기}) + \beta_{2}(\operatorname{장르}_{\operatorname{드라마}}) + \beta_{3}(\operatorname{이야기} \times \operatorname{장르}_{\operatorname{드라마}}) + \epsilon \]

조절관계를 lm()함수로 계산할 때 상호작용은 X*Z와 같은 방식으로 단축해 표현할 수 있다.

즉, 아래 두 회귀식은 동일하다.

lm(Y ~ X*Z, data)
lm(Y ~ X + Z + X:Z, data)

상호작용은 회귀모형 3개를 만들어 비교한다. 독립변수만 투입한 모형1, 독립변수와 조절변수를 함께 투입한 모형2, 독립변수와 조절변수가 상호작용하는 모형3을 만들어 결과를 비교해보자.

names(df) <- c("이야기", "친사회성", "장르")
y <- 2
x1 <- 1        # 친사회성 ~ 이야기  
x2 <- 3
xx <- c(x1,x2) # 친사회성 ~ 이야기 + 장르  
               # 친사회성 ~ 이야기 * 장르
### 회귀분석결과 표 생성 사용자함수
moderation_f <- function(df, y, x1, xx) {
## 변수 및 회귀모형
  # 변수
  dv <- names(df)[y]
  iv1 <- names(df)[x1]
  iv2 <- names(df)[xx]
  # 모형1 회귀식
  fml_mdl1 <- iv1 %>%
    paste0(., collapse = " + ") %>%
    paste0(dv, " ~ ", .)
  # 모형2 회귀식
  fml_mdl2 <- iv2 %>%
    paste0(., collapse = " + ") %>%
    paste0(dv, " ~ ", .)
  # 모형3 회귀식
  fml_mdl3 <- iv2 %>%
    paste0(., collapse = " * ") %>%
    paste0(dv, " ~ ", .)
## 회귀분석 + 데이터프레임결합
  model <- c(fml_mdl1, fml_mdl2, fml_mdl3)
  return(model)
} 
moderation_f(df, y, x1, xx) -> model
data.frame(Formulas = model) %>% gt()
Formulas
친사회성 ~ 이야기
친사회성 ~ 이야기 + 장르
친사회성 ~ 이야기 * 장르
 
nn <- length(xx) + 1 + 1  # IV행 + 절편행 + 상호작용항행 개수
model %>% 
  reg_f(nn, .) %>% 
  tbl_three(df, .)
친사회성에 대한 회귀분석결과1
IV Model 1 Model 2 Model 3
B SE p B SE p B SE p
(Intercept) 157.21 11.40 0.000 77.64 5.35 0.000 231.15 5.76 0.000
이야기 −0.01 0.04 0.876 0.01 0.02 0.563 −0.50 0.02 0.000
장르드라마


149.63 1.74 0.000 −150.55 8.05 0.000
이야기:장르드라마





1.00 0.03 0.000

R2
0.00

0.79

0.88

R2adj
0.00

0.79

0.88
1 N = 2000

모형1에서 독립변수를 단독으로 투입하면 회귀계수가 0에 수렴하고 통계적으로도 유의하지 않다(\(p\) < 0.876). 반면, 상호작용항(이야기:장르드라마)은 통계적으로 유의하다 (\(p\) < 0.001)

상호작용모형에서 회귀계수의 크기나 방향(양 or 음)은 해석하지 않는다. 산점도, 상자도, 선도 등으로 시각화하여 조절변수의 값에 따라 독립변수가 종속변수에 미치는 영향이 어떻게 변하는지 판단한다.

5.3.4.2 상호작용 사례2

상호작용은 조절변수의 속성에 따른 기울기가 반드시 반대방향일 필요는 없다. 기울기가 충분하게 차이만 나도 상호작용에 해당한다. ‘충분한 차이’ 여부는 상호작용 회귀모형에서 상호작용항의 통계적 유의성 여부로 판단한다.

N <- 1000
set.seed(37)
ivg1 <- rnorm(N, 300, 50)
set.seed(41)
ivg2 <- rnorm(N, 300, 50)
set.seed(43)
e <- rnorm(N, 30, 30)
df <- data.table(
  x = ivg1,  
  y = 50 + 0.8*ivg1 + e,
  z = rep("드라마", N)) %>% 
  bind_rows.(data.table(
  x = ivg2, 
  y = 120 + 0.3*ivg2 + e,  # 기울기 각도만 차이나게 설정
  z = rep("어드벤처", N))) 
viz_f(df, xlab = "이야기", ylab = "친사회성", zlab = "장르")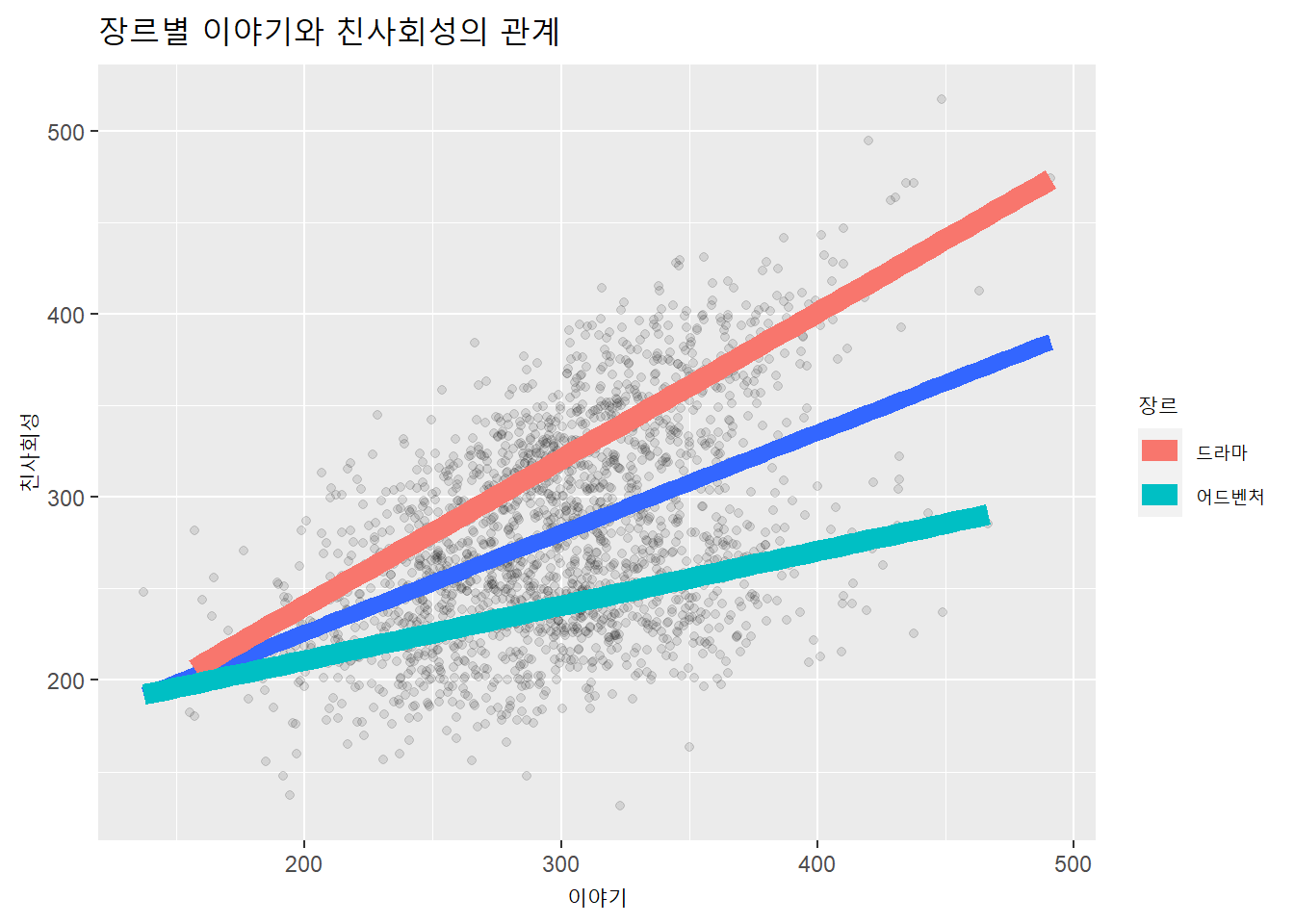

names(df) <- c("이야기", "친사회성", "장르")
y <- 2
x1 <- 1          # 친사회성 ~ 이야기  
x2 <- 3
xx <- c(x1, x2)  # 친사회성 ~ 이야기 + 장르  
                 # 친사회성 ~ 이야기 * 장르
nn <- length(xx) + 1 + 1  # IV행 + 절편행 + 상호작용항행 개수
moderation_f(df, y, x1, xx)  %>% 
  reg_f(nn, .) %>% 
  tbl_three(df, .)
친사회성에 대한 회귀분석결과1
IV Model 1 Model 2 Model 3
B SE p B SE p B SE p
(Intercept) 116.70 6.94 0.000 154.07 4.42 0.000 80.60 5.62 0.000
이야기 0.55 0.02 0.000 0.55 0.01 0.000 0.80 0.02 0.000
장르어드벤처


−79.81 1.45 0.000 70.55 8.05 0.000
이야기:장르어드벤처





−0.50 0.03 0.000

R2
0.22

0.69

0.74

R2adj
0.22

0.69

0.74
1 N = 2000

앞서 제시한 사례1과 달리, 이번에는 상호작용항이 없는 모형1과 모형2에서 독립변수의 종속변수에 대한 영향은 통계적으로 유의하다. 모형3의 상호작용항이 통계적으로 유의하므로 (\(p\) < 0.001), 상호작용 관계라고 판단할 수 있다. 실제로 위의 도표에서 조절변수(장르)의 값에 따라 독립변수와 종속변수 사이의 기울기가 현저하게 다르다.

5.3.5 매개관계

매개관계는 독립변수가 종속변수에 미치는 영향이 매개변수(Mediator)를 통해 이뤄지는 관계다.

dag_coords <-  # 좌표 데이터프레임
  data.table(
    name = c("IV", "Mediator", "DV"),
    x    = c(1, 2, 3),
    y    = c(1, 2, 1))
dagify(
  DV ~ IV,
  Mediator ~ IV,
  DV ~ Mediator,
  coords = dag_coords   # 좌표 지정
) %>% tidy_dagitty() %>% 
  ggplot(aes(
    x = x, xend = xend, y = y, yend = yend
  )) + xlim(0.7, 3.3) + ylim(0.7, 2.3) +
  geom_dag_point(color = "purple", alpha = .5, 
                 size = 15, shape = 15) +
  geom_dag_edges(edge_color = "purple") +
  geom_dag_text(color = "black") +
  labs(title = "매개관계") +
  theme_dag()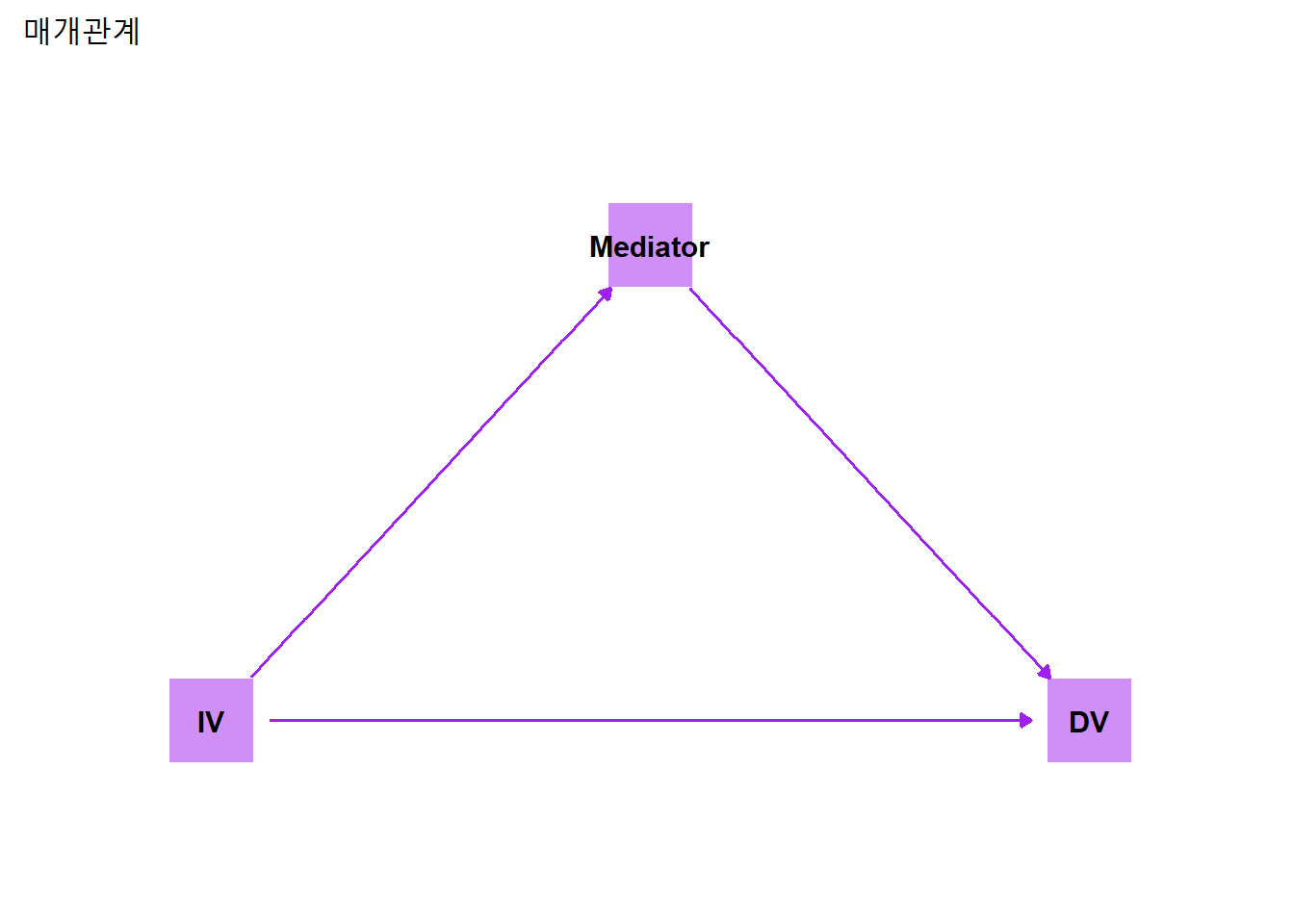

드라마이용과 친사회성의 관계를 예로 들어보자. 드라마를 많이 이용하면 친사회성이 증가한다고 할때, 드라마의 이용이 공감능력을 향상시키고, 이를 통해 친사회성이 증가하는 매개관계(드라마:drama → 공감:empathy → 친사회성:prosociality)를 표시해보자.

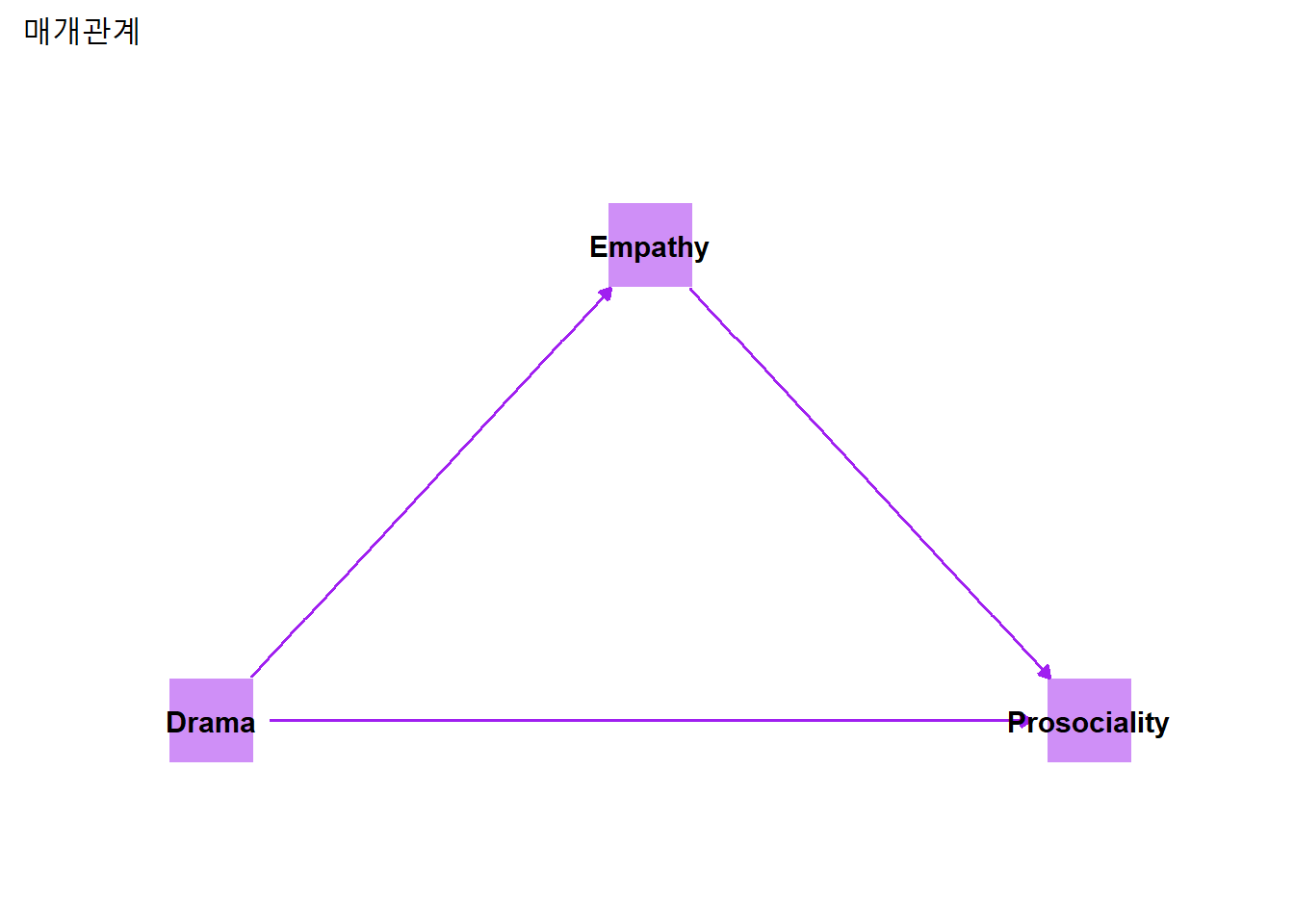
5.3.5.1 매개관계의 판단

매개관계(X → M → Y)를 보다 쉽게 이해하는 방법은 회귀모형을 3단계로 구분하는 것이다(Baron and Kenny 1986).

  • 1단계: X → Y 독립변수의 종속변수에 대한 회귀모형. 통계적으로 유의한 독립변수(\(X\))의 종속변수(\(Y\))에 대한 회귀계수 \(\beta_1\).매개변수를 통하지 않고 영향을 미쳤으므로 직접효과(direct effect)라고 한다.

\[Y = \alpha + \beta_1X + \epsilon\]

  • 2단계: X → M 독립변수의 매개변수에 대한 회귀모형. 통계적으로 유의한 독립변수(\(X\))의 매개변수(\(M\))에 대한 회귀계수 \(\beta_2\).

\[M = \alpha + \beta_2X + \epsilon\]

  • 3단계: X + M → Y 독립변수와 매개변수의 종속변수에 대한 회귀모형. 유의성이 사라진 독립변수(\(X\))의 종속변수(\(Y\))에 대한 회귀계수 \(\beta_3\)과 통계적으로 유의한 매개변수(\(M\))의 종속변수(\(Y\))에 대한 회귀계수 \(\beta_4\)

\[Y = \alpha + \beta_3X + \beta_4M + \epsilon\]

즉, 매개변수 \(M\)의 회귀계수 \(\beta_4\)가 통계적으로 유의한 상태에서, \(X\)의 회귀계수 \(\beta_3\)가 0에 수렴하거나 1단계의 \(X\)의 회귀계수 \(\beta_1\)에 비해 현저하게 감소하면 매개관계(\(X\) → \(M\) → \(Y\))가 성립된다.

3단계의 효과는 매개변수를 통해 영향을 미쳤으므로 간접효과(indirect effect)라고 한다.

직접효과와 간접효과를 합하면 총효과(total effect)가 된다.

  • 완전매개: 매개변수가 독립변수의 종속변수에 대한 영향을 온전하게 매개. 즉, 3단계에서 직접효과가 사라지는 관계. 직접효과가 온전하게 사라지므로 간접효과의 크기와 총효과의 크기가 비슷해진다.

  • 부분매개: 매개변수가 독립변수의 종속변수에 대한 영향을 일부만 매개. 즉, 3단계에서 직접효과가 현저하게 감소하는 관계.

5.3.5.2 매개관계 유의성 검정

직접효과, 간접효과, 총효과의 크기를 계산해 매개관계의 성립여부를 판단하기 위해서는 복잡한 계산이 필요하다. 다양한 방법이 소개돼 있는데, 여기서 소개하는 mediation패키지를 이용한 인과적매개분석이 그중 하나다(Imai, Keele, and Tingley 2010).

사용방법을 간략하게 정리하면 다음과 같다.

# 매개변수에 대한 회귀모형(2단계 회귀모형)
med.fit <- lm(MV ~ IV, data)
# 종속변수에 대해 회귀모형(3단계 회귀모형)
out.fit <- lm(DV ~ MV + IV, data)
# 두 회귀모형을 이용한 매개모형
fit <- mediate(med.fit, out.fit, 
               treat = "IV", mediator = "MV")
# 결과 요약
summary(fit)
# 결과 도표 출력
plot(fit)
  • ACME(Average Causal Mediation Effect): 간접효과(매개효과)
  • ADE(Average Direct Effect): 직접효과
  • Total Effect: 총효과

5.3.5.3 매개관계 사례

매개관계를 가상의 데이터셋으로 확인해보자.

N <- 1000
set.seed(37)
x <- runif(N, 10, 25)
set.seed(79)
e1 <- rnorm(N)
set.seed(421)
e2 <- rnorm(N)
m <- 1 + 0.5*x + e1
y <- 1 + 0.5*m + e2
df <- data.frame(y = y, x = x, m = m)

드라마이용이 공감능력을 향상시키고, 향상된 공감능력을 통해 친사회성이 증가하는 관계다.

df %>% 
  mutate(m2 = ifelse(m > mean(m), "상", "하")) %>% 
  ggplot() +
  geom_point(aes(x, y, color = m2), alpha = .2) +
  geom_smooth(aes(x, y, color = m2), size = 4,
              method = lm, se = F) +
  geom_smooth(aes(x, y), size = 2,
              method = lm, se = F) +
  labs(title = "매개관계 시각화",
       x = "드라마", y = "친사회성",
        color = "공감") +
  theme(plot.title = element_text(size = 17))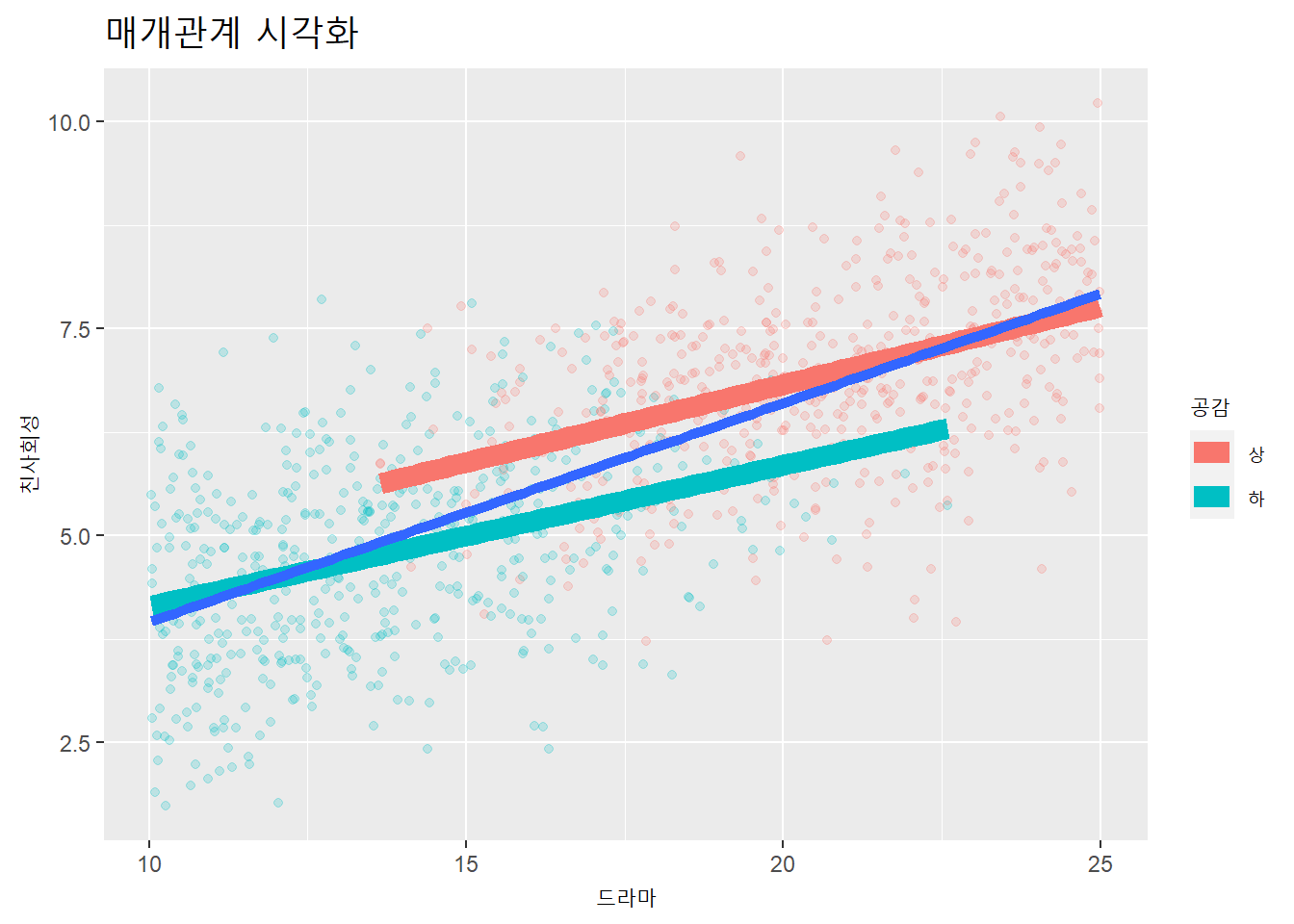

매개모형 판단의 3단계를 적용해 모형을 만들면 다음과 같다.

names(df) <- c("drama", "prosociality", "empathy")
y <- 2
x1 <- 1
m <- 3
xx <- c(x1, m)
nn <- length(xx) + 1
mediation_model <- function(df, y, x1, xx, m) {
## 변수 및 회귀모형
  # 변수
  dv <- names(df)[y]
  mv <- names(df)[m]
  iv1 <- names(df)[x1] 
  ivxx <- names(df)[xx] 
  # step 1 회귀식  # model1 x -> y
  fml_mdl1 <- iv1 %>%
    paste0(., collapse = " + ") %>%
    paste0(dv, " ~ ", .)
  # step 2 회귀식  # model2 x -> m  
  fml_mdl2 <- iv1 %>%
    paste0(., collapse = " + ") %>%
    paste0(mv, " ~ ", .)
  # step 3 회귀식  # model3 x + m -> y
  fml_mdl3 <- ivxx %>%
    paste0(., collapse = " + ") %>%
    paste0(dv, " ~ ", .)
## 회귀분석 + 데이터프레임결합
  model <- c(fml_mdl1, fml_mdl2, fml_mdl3)
  return(model)
}
mediation_model(df, y, x1, xx, m) -> model
data.frame(Formulas = model) %>% gt()
Formulas
prosociality ~ drama
empathy ~ drama
prosociality ~ drama + empathy

3단계 매개분석 결과을 저장한 데이터프레임을 행방향으로 결합하므로, 사용자 함수 수정이 필요하다.

### 회귀분석 사용자함수
reg_mediation <- function(nn, model){  
  # 표의 행 개수: 모형2 변수 + 절편행 개수
  output <- list()
  for (i in seq_along(model)) {
    fit <- df %>% lm(model[i], .)
    # 변수명, 회귀계수, 표준오차 데이터프레임
    op <- tidy(fit)[, -4] %>% # statitic만 빼고 모두 선택
      # 결정계수 데이터프레임
      bind_rows.(data.frame(
        term = c("결정계수",
                 "수정결정계수"),
        estimate = NA,
        std.error = c(summary(fit)$r.squared,
                     summary(fit)$adj.r.squared),
        p.value = NA
      ))
    output <- list(output, op)
  }
  return(output)
}
(reg_mediation(nn, model) -> fit)
## [[1]]
## [[1]][[1]]
## [[1]][[1]][[1]]
## list()
## 
## [[1]][[1]][[2]]
## # A tidytable: 4 x 4
##   term         estimate std.error    p.value
##   <chr>           <dbl>     <dbl>      <dbl>
## 1 (Intercept)      5.77    0.365   1.72e- 50
## 2 drama            1.96    0.0598  7.49e-160
## 3 결정계수        NA       0.517  NA        
## 4 수정결정계수    NA       0.516  NA        
## 
## 
## [[1]][[2]]
## # A tidytable: 4 x 4
##   term         estimate std.error    p.value
##   <chr>           <dbl>     <dbl>      <dbl>
## 1 (Intercept)      2.53    0.177   4.47e- 42
## 2 drama            1.22    0.0291  5.39e-221
## 3 결정계수        NA       0.636  NA        
## 4 수정결정계수    NA       0.635  NA        
## 
## 
## [[2]]
## # A tidytable: 5 x 4
##   term         estimate std.error    p.value
##   <chr>           <dbl>     <dbl>      <dbl>
## 1 (Intercept)    1.59      0.238   3.68e- 11
## 2 drama         -0.0518    0.0590  3.80e-  1
## 3 empathy        1.65      0.0387  2.58e-227
## 4 결정계수      NA         0.829  NA        
## 5 수정결정계수  NA         0.829  NA

매개분석 과정에서 3단계 회귀모형은 매개변수를 종속변수로 분석하기 때문에 표를 표시하는 방법을 수정해야 한다. 각 단계가 순차적으로 보이도록 데이터프레임을 행방향으로 결합한다.

## 모형3개 결합해 표로 정리
tbl_mediation <- function(df, fit){
  # 회귀분석 결과에 단계를 표하는 열 생성해 열 결합.
  data.frame(step = "Step1") %>% bind_cols.(fit[[1]][[1]][[2]]) %>%
    bind_rows.(data.frame(step = "Step2") %>% bind_cols.(fit[[1]][[2]])) %>%
    bind_rows.(data.frame(step = "Step3") %>% bind_cols.(fit[[2]])) %>%
    gt() %>%
    tab_header(str_glue("3단계 매개모형")) %>%
    fmt_number(3:5, decimals = 2) %>%
    fmt_number(starts_with("p"), decimals = 3) %>%  # p값만 소숫점 3자리 표시
    fmt_missing(3:5, missing_text = html("<br>")) %>%
    cols_label(
      step = html("<br>"),   # 단계 표시 step열 이름 미표시
      term = md("IV"),
      estimate = md("_B_"),
      std.error = md("_SE_"),
      p.value = md("_p_")) %>%
    tab_row_group(    # 각 회귀분석 단계별 그룹 지정
      label = str_glue("Step 3: {names(df)[y]} ~ {names(df)[x1]} + {names(df)[m]}"),
      rows = step == "Step3") %>% 
    tab_row_group(
      label = str_glue("Step 2: {names(df)[m]} ~ {names(df)[x1]}"),
      rows = step == "Step2") %>% 
    tab_row_group(
      label = str_glue("Step 1: {names(df)[y]} ~ {names(df)[x1]}"),
      rows = step == "Step1") %>% 
    text_transform(   # 결정계수를 통계기호로 변경
      locations = 
        cells_body(
          columns = term,
          rows = term == "결정계수"),
      fn = function(x) {html(
          "<p align='center'><em>R<sup>2</sup></em></p>")
        }) %>% 
    text_transform(
      locations = 
        cells_body(
          columns = term,
          rows = term == "수정결정계수"),
      fn = function(x) {html(
          "<p align='center'><em>R<sup>2</sup><sub>adj</sub></em></p>")
        }) %>% 
    text_transform(  # step열의 글자를 공백으로 변경
      locations = 
        cells_body(
          columns = step,
          rows = step == "Step1"),
      fn = function(x) html("<br>")) %>% 
    text_transform(
      locations = 
        cells_body(
          columns = step,
          rows = step == "Step2"),
      fn = function(x) html("<br>")) %>% 
    text_transform(
      locations = 
        cells_body(
          columns = step,
          rows = step == "Step3"),
      fn = function(x) html("<br>")) %>% 
    tab_footnote(
      footnote = str_glue("N = {nrow(df)}"),
      locations = cells_title())
}
model %>% 
  reg_mediation(nn, .) %>% 
  tbl_mediation(df, .)
3단계 매개모형1

IV B SE p
Step 1: prosociality ~ drama

(Intercept) 5.77 0.36 0.000

 drama 1.96 0.06 0.000

R2
0.52

R2adj
0.52
Step 2: empathy ~ drama

(Intercept) 2.53 0.18 0.000

 drama 1.22 0.03 0.000

R2
0.64

R2adj
0.64
Step 3: prosociality ~ drama + empathy

(Intercept) 1.59 0.24 0.000

 drama −0.05 0.06 0.380

 empathy 1.65 0.04 0.000

R2
0.83

R2adj
0.83
1 N = 1000

1단계 모형에서 통계적으로 유의한 독립변수 drama의 prosociality에 대한 관계(\(\beta\) = 1.96, \(p\) < 0.001)는 3단계에서 사라진다(\(\beta\) = -0.05, \(p\) = 0.380). 반면, 매개변수 empathy의 prociality에 대한 관계는 통계적으로 유의하다(\(\beta\) = 1.65, \(p\) < 0.001).

매개모형이 성립하는지 판단하기 위해 mediation패키지의 mediate()함수로 간접효과의 유의성을 계산해보자.

set.seed(37)
names(df)
## [1] "drama"        "prosociality" "empathy"
m1 <- lm(empathy ~ drama, df)
m2 <- lm(prosociality ~ drama + empathy, df)
fit <- mediate(m1, m2, treat = "drama", mediator = "empathy")
plot(fit)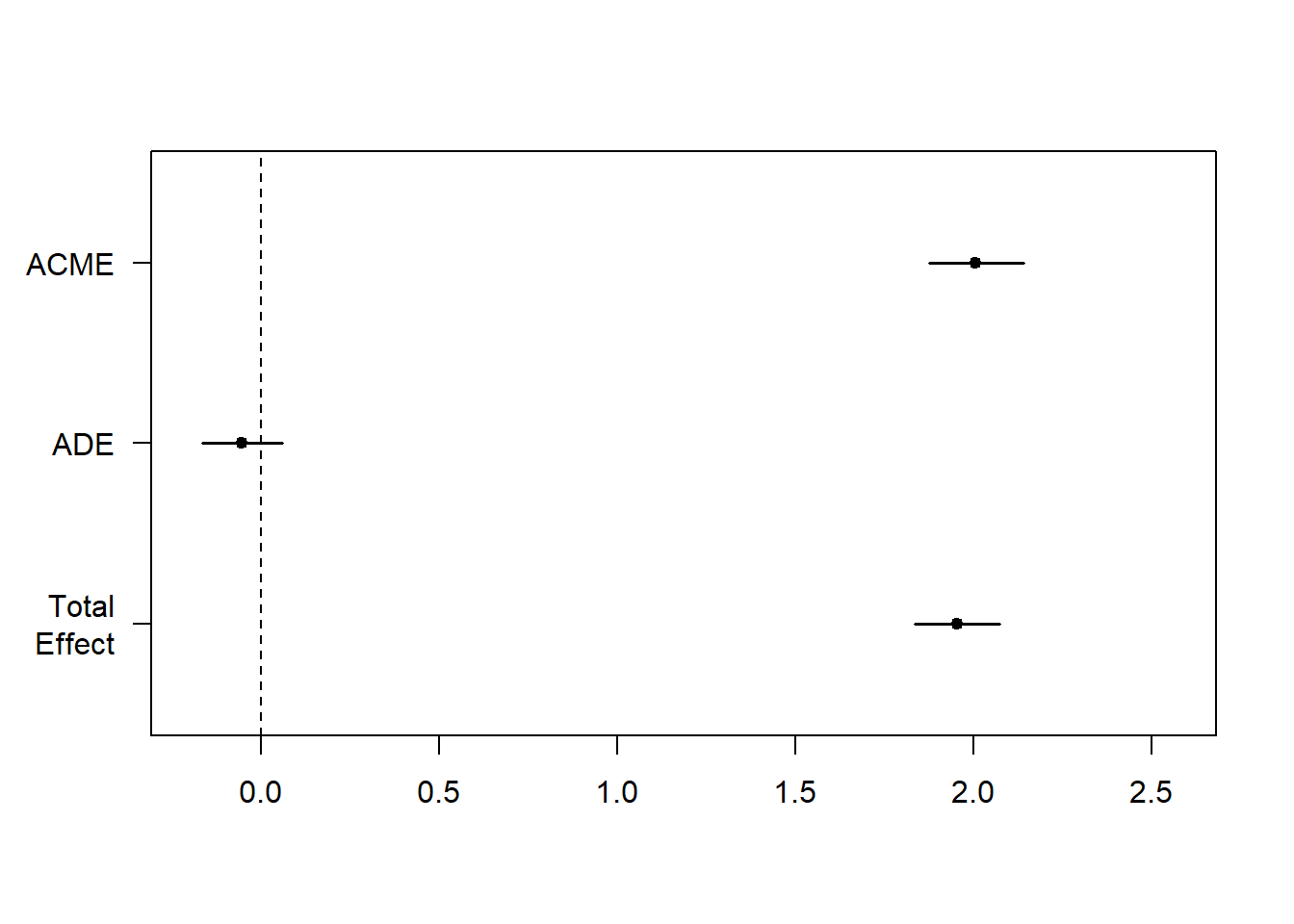

총효과(Total Effect)와 간접효과(ACME)가 비슷하고, 직접효과(ADE)는 사라졌다.

summary(fit)
## 
## Causal Mediation Analysis 
## 
## Quasi-Bayesian Confidence Intervals
## 
##                Estimate 95% CI Lower 95% CI Upper p-value    
## ACME              2.005        1.876         2.14  <2e-16 ***
## ADE              -0.052       -0.164         0.06    0.37    
## Total Effect      1.953        1.834         2.07  <2e-16 ***
## Prop. Mediated    1.026        0.970         1.09  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Sample Size Used: 1000 
## 
## 
## Simulations: 1000

총효과(Total Effect)의 계수 1.953에서 직접효과(ADE)의 계수 -0.052를 제하면 간접효과(ACEM)의 계수 2.005가 나온다.

간접효과(\(\beta_{ACME}\) = 2.005)는 통계적으로 유의하게 0과 다르고(\(p\) < 0.001), 직접효과(\(\beta_{ADE}\) = -0.052)는 0과 유의하게 다르지 않다(\(p\) = 0.37).

회귀계수가 0이면 변수와 변수 사이에 연관성이 없다는 의미다.

이 결과를 통해 드라마 이용은 공감능력을 향상시키고, 이를 통해 친사회성이 증가한다고 판단할수 있다 (주의: 가상의 데이터셋이다.)

5.3.5.4 부분 매개

매개변수가 독립변수의 종속변수에 대한 영향을 부분만 매개하는 경우. 모형의 매개변수 외에 측정되지 않는 또 다른 매개변수가 있을때 나타나는 현상.

완전매개

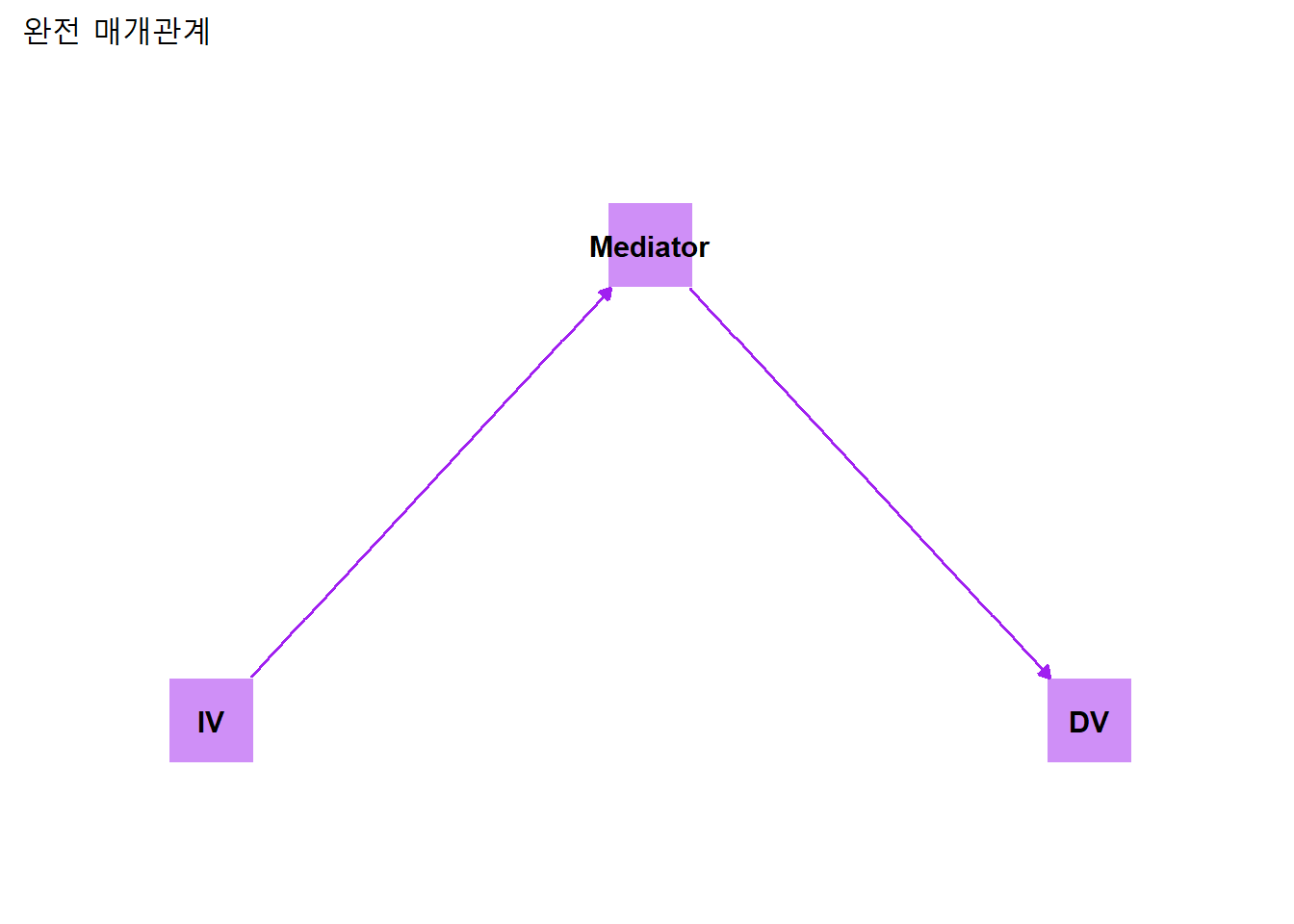
부분매개

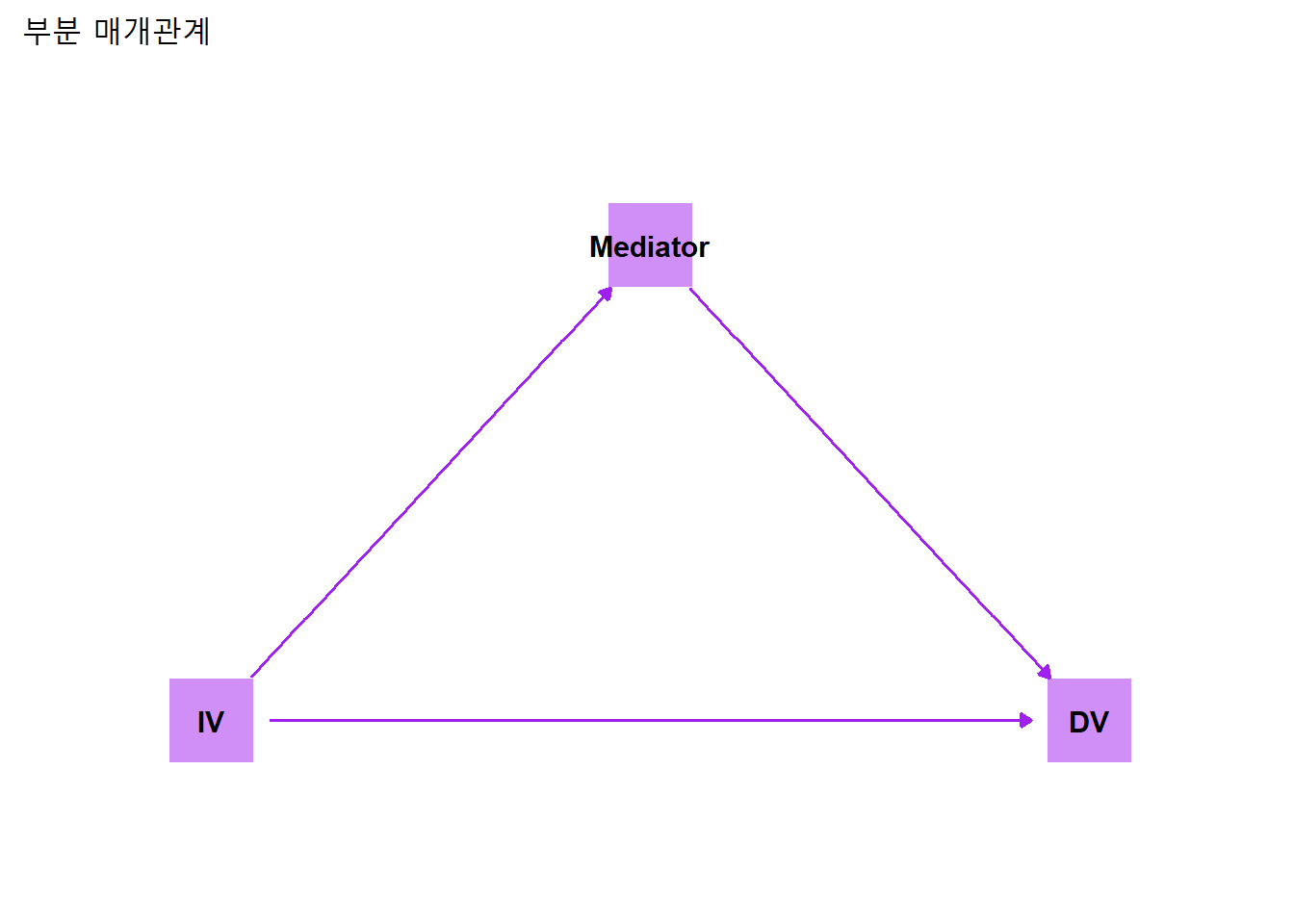
부분매개가 완전매개를 포괄하므로, 매개관계를 관계도로 나타낼때는 부분매개관계로로 제시한다.

5.3.5.5 부분매개 사례

완전 매개 사례의 종속변수에 독립변수가 직접적으로 영향을 주는 값을 생성에 종속변수와 합산해 가상 데이터셋을 만든다.

N <- 1000
set.seed(37)
x <- runif(N, 10, 25)
set.seed(79)
e1 <- rnorm(N)
set.seed(421)
e2 <- rnorm(N)
set.seed(73)
e3 <- rnorm(N)

m <- 1 + 0.3*x + e1
y1 <- 1 + 0.3*m + e2  # 매개변수 통한 간접효과 경로
y2 <- 1 + 0.2*x + e3  # 매개변수 통하지 않는 직접효과 경로 
y <- y1 + y2

df <- data.frame(y = y, x = x, m = m)  
df %>% 
  mutate(m2 = ifelse(m > mean(m), "상", "하")) %>% 
  ggplot() +
  geom_point(aes(x, y, color = m2), alpha = .2) +
  geom_smooth(aes(x, y, color = m2), size = 4,
              method = lm, se = F) +
  geom_smooth(aes(x, y), size = 2,
              method = lm, se = F) +
  labs(title = "매개관계 시각화",
       x = "드라마", y = "친사회성",
        color = "공감") +
  theme(plot.title = element_text(size = 17))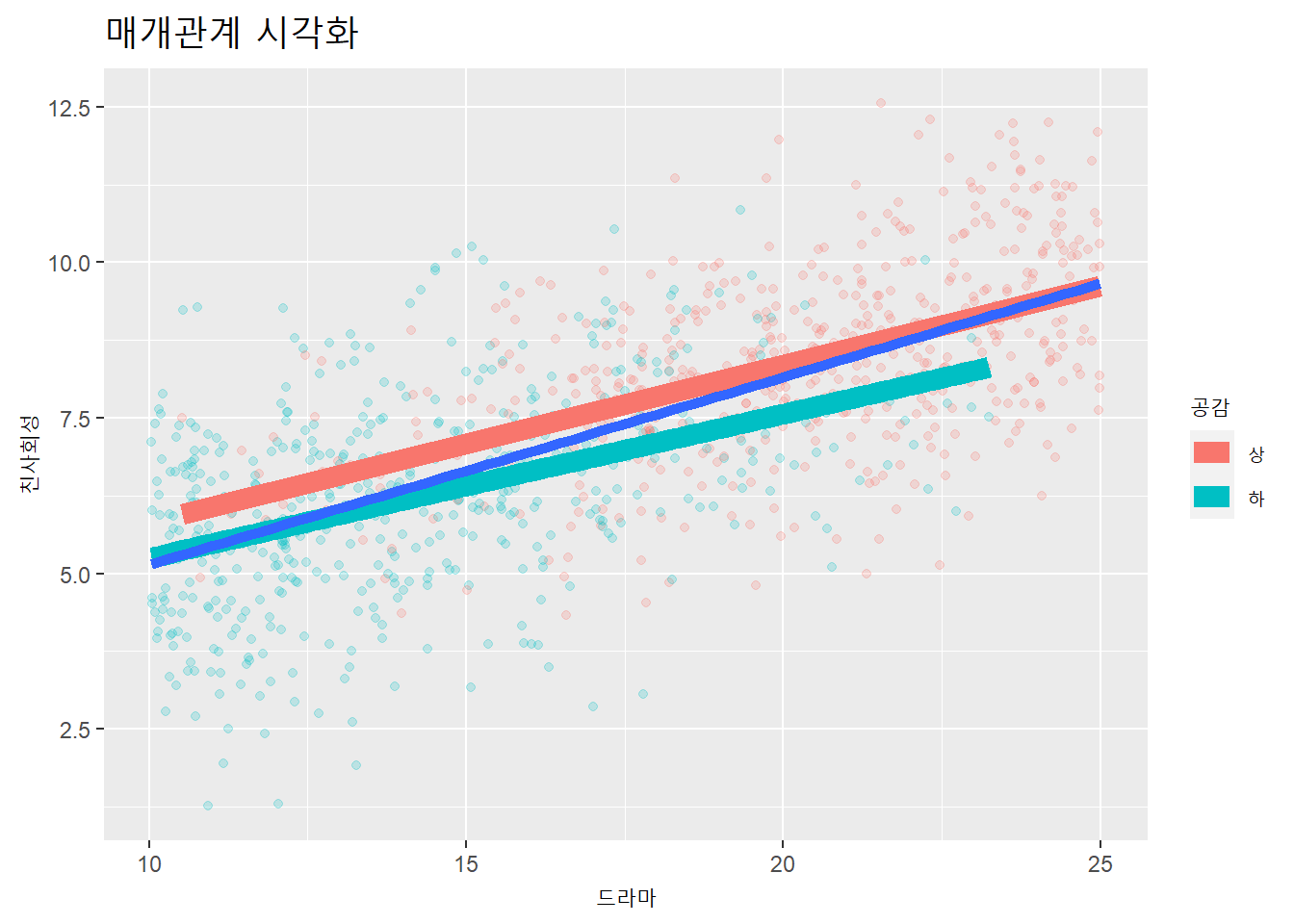

매개모형 판단의 3단계를 적용해 모형을 만들면 다음과 같다.

names(df) <- c("drama", "prosociality", "empathy")
y <- 2
x1 <- 1
m <- 3
xx <- c(x1, m)
nn <- length(xx) + 1
mediation_model(df, y, x1, xx, m) -> model
data.frame(Formulas = model) %>% gt()
Formulas
prosociality ~ drama
empathy ~ drama
prosociality ~ drama + empathy

생성한 모형으로 회귀분석을 3단계 실시해 표로 정리.

model %>% 
  reg_mediation(nn, .) %>% 
  tbl_mediation(df, .)
3단계 매개모형1

IV B SE p
Step 1: prosociality ~ drama

(Intercept) 6.10 0.40 0.000

 drama 1.52 0.05 0.000

R2
0.46

R2adj
0.46
Step 2: empathy ~ drama

(Intercept) 1.97 0.16 0.000

 drama 0.58 0.02 0.000

R2
0.44

R2adj
0.44
Step 3: prosociality ~ drama + empathy

(Intercept) 2.90 0.33 0.000

 drama 0.58 0.05 0.000

 empathy 1.62 0.06 0.000

R2
0.68

R2adj
0.68
1 N = 1000

1단계 모형에서 통계적으로 유의한 독립변수 drama의 prosociality에 대한 관계(\(\beta\) = 1.5, \(p\) < 0.001)가 3단계에서 회귀계수만 감소하고 유의성은 사라지지 않는다(\(\beta\) = 0.58, \(p\) < 0.001). 매개변수 empathy의 prociality에 대한 관계는 통계적으로 유의하다(\(\beta\) = 1.62, \(p\) < 0.001).

회귀계수의 감소(즉, 매개변수의 영향)가 유의한지는 간접효과의 유의성을 계산해 판단할 수 있다. mediation패키지의 mediate()함수로 간접효과의 유의성을 계산해보자.

set.seed(37)
names(df)
## [1] "drama"        "prosociality" "empathy"
m1 <- lm(empathy ~ drama, df)
m2 <- lm(prosociality ~ drama + empathy, df)
fit <- mediate(m1, m2, treat = "drama", mediator = "empathy")
plot(fit)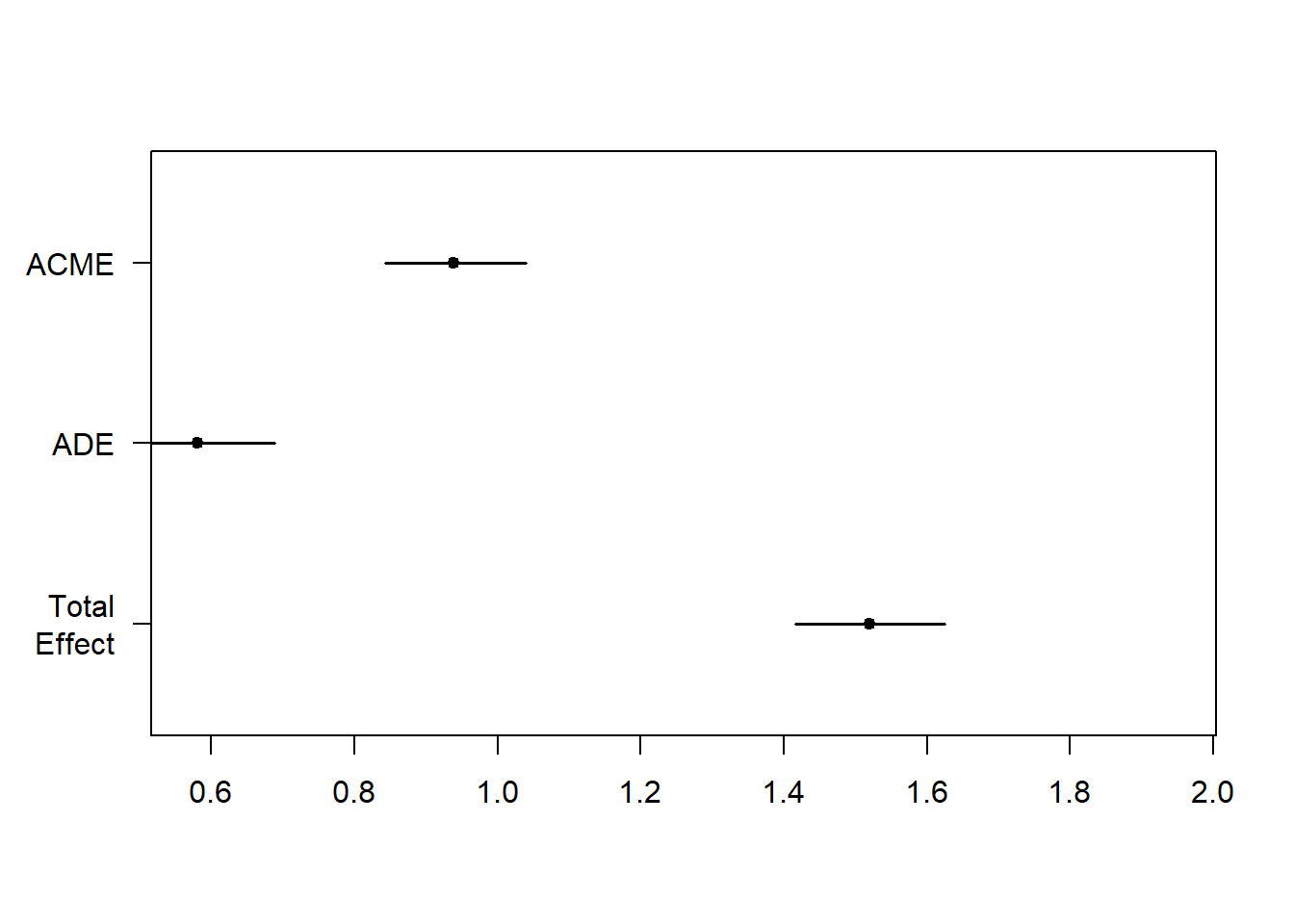

직접효과가 사라지지 않았지만, 간접효과가 더 크다.

summary(fit)
## 
## Causal Mediation Analysis 
## 
## Quasi-Bayesian Confidence Intervals
## 
##                Estimate 95% CI Lower 95% CI Upper p-value    
## ACME              0.939        0.844         1.04  <2e-16 ***
## ADE               0.581        0.476         0.69  <2e-16 ***
## Total Effect      1.520        1.416         1.62  <2e-16 ***
## Prop. Mediated    0.618        0.561         0.68  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Sample Size Used: 1000 
## 
## 
## Simulations: 1000

총효과(Total Effect)의 계수 1.52에서 직접효과(ADE)의 계수 0.581를 제하면 간접효과(ACEM)의 계수 0.939가 나온다.

직접효과(\(\beta_{ADE}\) = 0.581)는 0과 유의하게 다르지 않다(\(p\) < 0.001). 간접효과(\(\beta_{ACME}\) = 0.939)는 통계적으로 유의하게 0과 다르다(\(p\) < 0.001),

따라서, 직접효과가 유의하기때문에 매개변수가 독립변수의 영향을 완전하게 매개하지는 않아도 간접효과가 유의하므로 매개변수가 독립변수의 종속변수에 대한 영향을 부분적으로 매개한다고 판단할 수 있다.

5.4 종합

5.4.1 과학

  • 체계적논리
  • 체계적경험(수집+측정)
  • 이론(원인과 결과의 관계)

5.4.2 통계

  • 심슨의 역설(Simpson’s paradox)
  • 더미변수(dummy variable: 가변수)
  • 통계적 유의성
  • p값
  • 모집단(population)
  • 표본(sample)
  • 표집(sampling)
  • 추론통계(inferential statistics)
  • 기술통계(descriptive statistics)
  • 허위관계(spurious relations)
  • 혼란변수(confounder: 혼동변수, 교란변수)
  • 충돌변수(collider)
  • 합산관계(두개 이상의 원인)
  • 상호작용(interaction)
  • 조절변수(moderator)
  • 역인과관계
  • 인과관계
  • 매개변수(mediator)
  • 직접효과(ADE: Average Direct Effect)
  • 간접효과(ACME: Average Causal Mediation Effect)
  • 총효과(Total Effect)
  • 매개분석 3단계
  • 완전매개
  • 부분매개

5.4.3 코딩

  • ggdag
    • dagify()
    • ggdag()
    • theme_dag()
    • ggdag_adjust()
    • tidy_dagitty()
    • geom_dag_point()
    • geom_dag_edges()
    • geom_dag_text()
  • gt
    • tab_header()
    • fmt_number()
    • fmt_missing()
    • starts_with()
    • tab_spanner()
    • text_transform()
    • text_footnote()
  • html
    • <br>
    • <p align=“center”> </p>
    • <em> </em>
    • <sup> </sup>
    • <sub> </sub>
  • mediation
    • mediate()

5.5 연습

  1. 화가 김동유의 작품을 검색해 그의 그림의 의미를 실재와 인식의 틀에서 설명하시오.

  2. 아래 주어진 데이터셋은 가상의 상황을 상정해 만든 100행 3열의 데이터프레임이다. 행복을 종속변수로 설정해 분석하여, 어느 모형(허위관계, 충돌관계, 합산모형, 상호작용, 매개관계)에 해당하는지 밝히시오.

  • 인과모형에서 학습한 통계기법을 이용해 분석하시오.
  • 분석결과는 산점도와 선도로 시각화하고, gt패키지 표로 정리.
  • 만일 매개관계에 해당한다면 mediation 패키지로 매개변수 유의성 검정 수행.
url <- "https://raw.githubusercontent.com/dataminds/art/main/files/mediation.csv"
rio::import(url) -> df
names(df) <- c("성적", "성취감", "행복")

References

Baron, Reuben M, and David A Kenny. 1986. “The Moderator–Mediator Variable Distinction in Social Psychological Research: Conceptual, Strategic, and Statistical Considerations.” Journal of Personality and Social Psychology 51 (6): 1173.
Imai, Kosuke, Luke Keele, and Dustin Tingley. 2010. “A General Approach to Causal Mediation Analysis.” Psychological Methods 15 (4): 309.
Kievit, Rogier, Willem Eduard Frankenhuis, Lourens Waldorp, and Denny Borsboom. 2013. “Simpson’s Paradox in Psychological Science: A Practical Guide.” Frontiers in Psychology 4: 513.
Pearl, Judea, and Dana Mackenzie. 2018. The Book of Why: The New Science of Cause and Effect. Basic books.
Simpson, E. H. 1951. “The Interpretation of Interaction in Contingency Tables.” Journal of the Royal Statistical Society: Series B (Methodological) 13 (2): 238–41.
안도현. 2021. “유령위험과 무시된 위해: 위험의 개념화와 유형화.” 언론정보연구 58 (2): 5–65.