8 평균비교

c(
  "rio", "tidyverse", "tidytable", "psych", "psychTools", 
  "skimr", "janitor", "tidymodels", "lm.beta", "mediation",
  "GGally", "ggforce", "mdthemes", "patchwork", "ggdag",
  "r2symbols", "equatiomatic", "gt" 
  ) -> pkg 
sapply(pkg, function(x){
  if(!require(x, ch = T)) install.packages(x, dependencies = T)
  library(x, ch = T)
})

내가 갖고 있는 자료에서 나타난 효과(예: 평균의 차이)가 실재를 반영한 것인가, 아니면 우연에 의한 허상인가?

실재를 반영했다면 진양성 혹은 진음성이고, 우연에 의한 허상이라면 1종오류(위양성) 혹은 2종오류(위음성)다.

실상과 허상 가능성 판단에 널리 사용되는 방법이 영가설 검정(Null Hypothesis Testing)이다.

모집단에 ’효과’가 없다고 가정한 영가설을 기각해 대립가설을 채택하거나 영가설을 기각하지 않고 영가설 유지함으로써 내가 갖고 있는 자료에서 관측한 효과가 ’실재의 반영’인지 ’우연에 의한 허상’인지 판단한다.

양성(영가설 기각)으로 판단해 대립가설을 채택하거나, 음성(영가설 미기각)으로 판단해 영가설을 유지하는 경우, 어느 상황이건 오류 가능성이 있다. 즉, 양성(효과 있음) 혹은 음성(효과 없음)의 판단은 100% 확실성이 있는게 아니므로 확률적으로 접근한다.

통상 오류가능성은 통계적 유의도(= 유의확률: \(p\)값)로 판단한다. 널리 사용하는 판단기준은 유의수준(significant level: \(\alpha\))이다. 관행적으로 유의수준을 0.05로 잡는다. (따라서 맥락에 따라 유의수준은 더 혹은 덜 엄격하게 적용할 필요가 있다.)

관행적으로 \(p\)값이 0.05보다 같거나 작으면, 관측한 효과가 우연일 가능성이 낮다고 판단해 영가설을 기각해 대립가설을 채택한다. 반면, \(p\)값이 0.05보다 크면, 관측한 효과가 우연일 가능성이 높다고 판단해 영가설을 기각하지 않고 영가설을 유지한다.

8.1 이론 vs. 시뮬레이션

영가설검정에 필요한 \(p\)값 계산에는 이론으로 접근하는 방식과 시뮬레이션으로 접근하는 방식이 있다. 두 접근의 차이는 통계치를 구하는 방식이다. 이론기반은 공식을 적용해 통계치를 구하고, 시뮬레이션 기반은 무수히 많은 가상의 표본을 만들어 통계치를 구한다.

dag_coords <-
  data.table(
    name = c("Specify_Variables", "Hypothesize_Ho", "Generate_Data", "Calculate_Statistic"),
    x = c(1, 2, 3, 4),
    y = c(4, 3, 2, 1))

dagify(
  Calculate_Statistic ~ Generate_Data,
  Generate_Data ~ Hypothesize_Ho,
  Hypothesize_Ho ~ Specify_Variables,
  coords = dag_coords
) %>% tidy_dagitty() %>% 
  ggplot(aes(x = x, xend = xend, y = y, yend = yend)) +
  xlim(0.5, 4.5) + ylim(0.5, 4.4) +
  geom_dag_point(color = "DeepPink", alpha = .2,
                 size = 15, shape = 15) +
  geom_dag_edges(edge_color = "DeepPink" ) +
  geom_dag_text(color = "black") +
  labs(title = "가설검정 구조: 시뮬레이션기반") +
  theme_dag()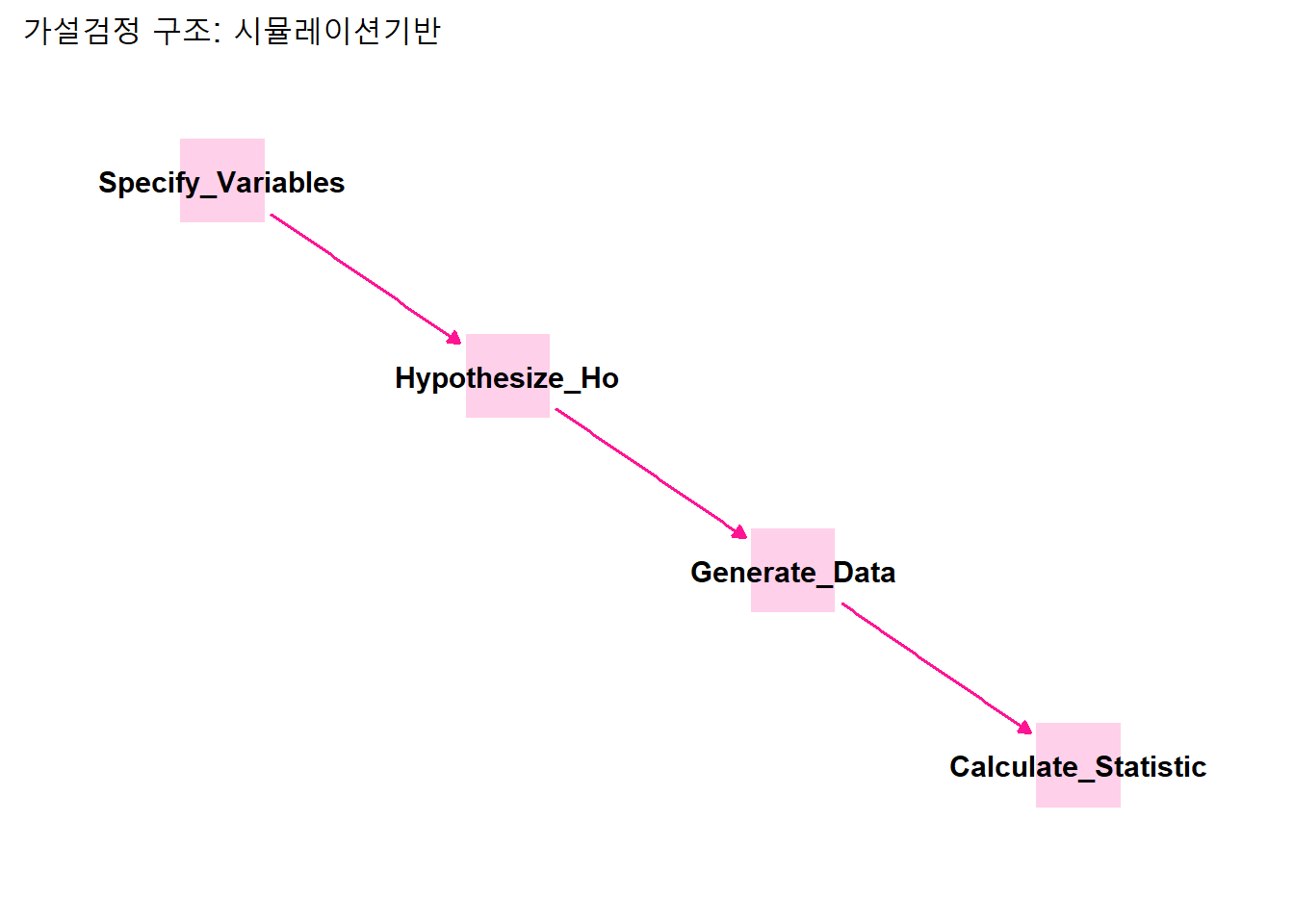

dag_coords <-
  data.table(
    name = c("Specify_Variables", "Hypothesize_Ho",  "Calculate_Statistic"),
    x = c(1, 2, 3),
    y = c(3, 2, 1))

dagify(
  Calculate_Statistic ~ Hypothesize_Ho,
  Hypothesize_Ho ~ Specify_Variables,
  coords = dag_coords
) %>% tidy_dagitty() %>% 
  ggplot(aes(x = x, xend = xend, y = y, yend = yend)) +
  xlim(0.5, 3.5) + ylim(0.5, 3.4) +
  geom_dag_point(color = "DarkGreen", alpha = .2,
                 size = 15, shape = 15) +
  geom_dag_edges(edge_color = "DarkGreen" ) +
  geom_dag_text(color = "black") +
  labs(title = "가설검정 구조: 이론기반") +
  theme_dag()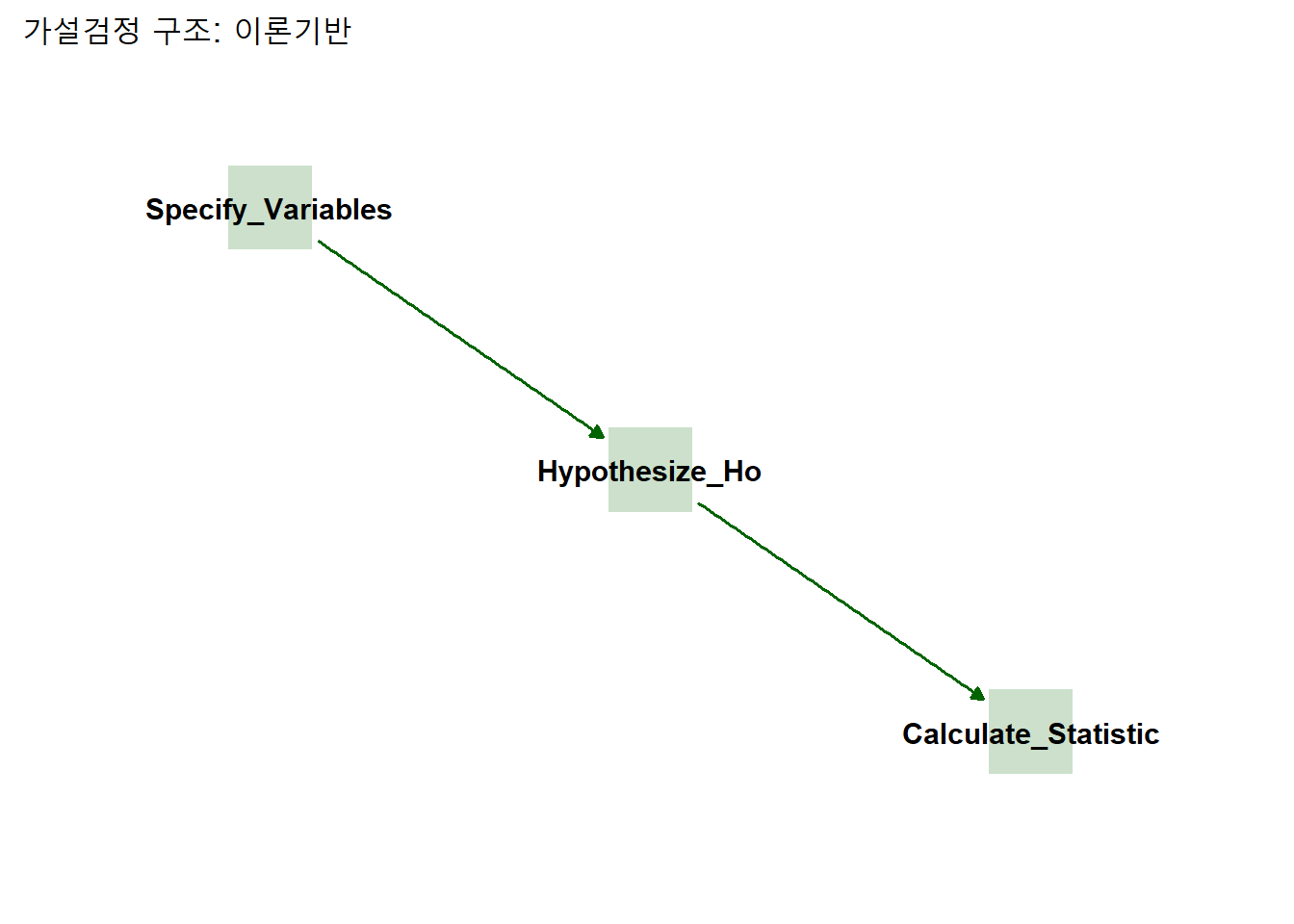

이 원리를 잘 구현한게 infer패키지다.

specify() : 관심 변수 설정
hypothesize() : 영가설 지정
generate() : (시뮬레이션기반인경우) 모의자료 생성
calculate() : 통계치 계산

infer패키지에서 제공하는 gss데이터셋을 이용해 이론기반 가설검정과 시뮬레이션기반 가설검정에 대해 알아보자.

GSS(The General Social Survey)는 미국에서 1972년부터 매년 실시하는 사회 및 여론조사다. gss데이터셋에는 표본 500명 변수 11개가 포함돼 있다.

gss %>% glimpse()

## Rows: 500
## Columns: 11
## $ year    <dbl> 2014, 1994, 1998, 1996, 1994, 1996, 1990, 2016, 2000, 1998, 20~
## $ age     <dbl> 36, 34, 24, 42, 31, 32, 48, 36, 30, 33, 21, 30, 38, 49, 25, 56~
## $ sex     <fct> male, female, male, male, male, female, female, female, female~
## $ college <fct> degree, no degree, degree, no degree, degree, no degree, no de~
## $ partyid <fct> ind, rep, ind, ind, rep, rep, dem, ind, rep, dem, dem, ind, de~
## $ hompop  <dbl> 3, 4, 1, 4, 2, 4, 2, 1, 5, 2, 4, 3, 4, 4, 2, 2, 3, 2, 1, 2, 5,~
## $ hours   <dbl> 50, 31, 40, 40, 40, 53, 32, 20, 40, 40, 23, 52, 38, 72, 48, 40~
## $ income  <ord> $25000 or more, $20000 - 24999, $25000 or more, $25000 or more~
## $ class   <fct> middle class, working class, working class, working class, mid~
## $ finrela <fct> below average, below average, below average, above average, ab~
## $ weight  <dbl> 0.8960034, 1.0825000, 0.5501000, 1.0864000, 1.0825000, 1.08640~

대학학위(college) 유무와 노동시간(hours)의 관계에 대한 가설검정을 해보자.

\(H_0\): 대학학위보유 노동시간 = 대학학위 미보유 노동시간

gss %>% select.(college, hours) -> df; df %>% skim()

Table 8.1: Data summary
Name	Piped data
Number of rows	500
Number of columns	2
Key	NULL
_______________________
Column type frequency:
factor	1
numeric	1
________________________
Group variables	None

Variable type: factor

skim_variable	n_missing	complete_rate	ordered	n_unique	top_counts
college	0	1	FALSE	2	no : 326, deg: 174

Variable type: numeric

skim_variable	n_missing	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
hours	0	1	41.38	14.82	3	36.75	40	48	89	▂▂▇▂▁

먼저 기술통계부터 구한다.

df %>% 
  ggplot(aes(college, hours, color = college)) +
  geom_sina(alpha = 0.3) +
  geom_text(stat = 'summary',
            aes(label = paste("평균", round(..y.., 2), "시간")),
            color = 'black', size = 4) +
  labs(title = "대학학위유무별 노동시간 평균과 분포",
       x = "대학학위 유무",
       y = "주당 노동시간") + theme(legend.position = 'none')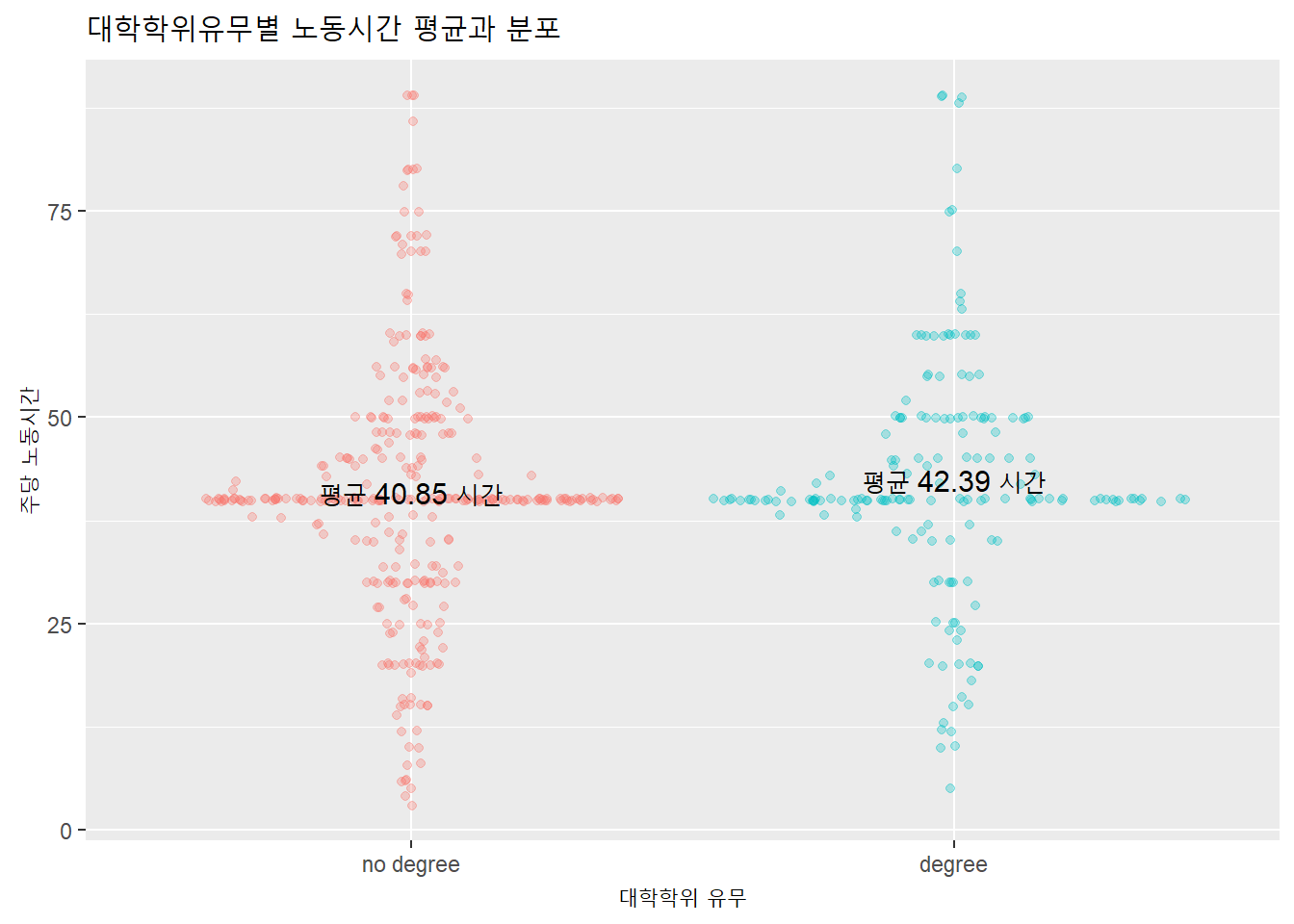

밀도도표로 학위 유무에 따른 노동시간의 분포를 시각화해보자.

df %>% ggdensity(x = 'hours', 
                 add = 'mean', 
                 rug = T,
                 color = 'college', fill = 'college')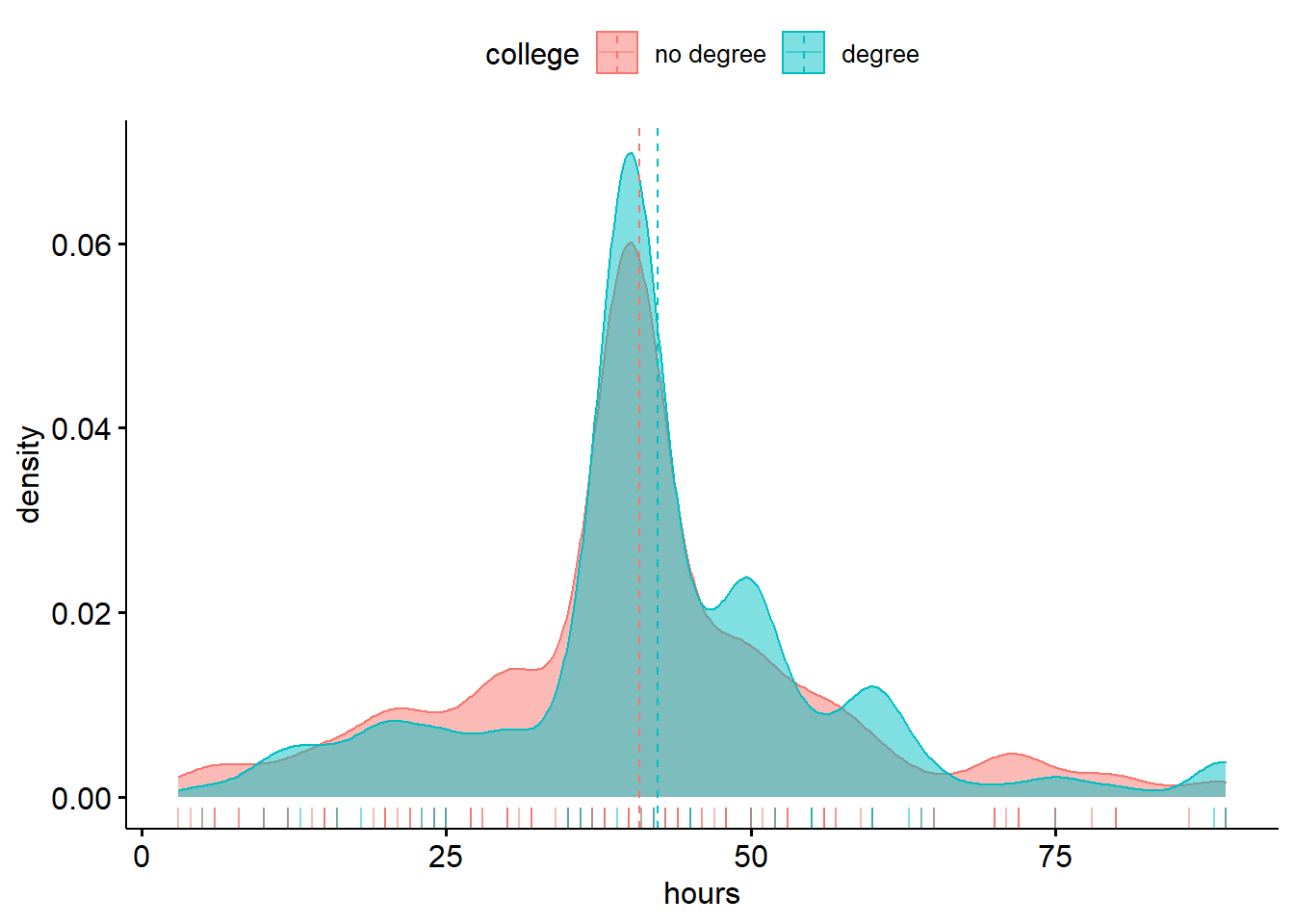

8.1.1 이론기반 가설검정

이론기반 가설검정에서는 공식을 이용해 \(t\)통계치을 구한 다음, \(t\)분포 상의 \(p\)값을 구한다. 요즘은 소프트웨어로 \(p\)값을 계산하지만, 과거에는 \(t\)분포표에서 수작업으로 \(p\)근사값을 찾았다.

\(t\)통계치을 이용하기에 \(t\)검정이라고 한다.

\[ t = \dfrac{집단간평균차이}{각집단분산의 합} \] \(t\)통계치를 구하는 공식은 다음과 같다.

\[ t = \dfrac{ \overline{x}_1 - \overline{x}_2}{ \sqrt{\dfrac{{s_1}^2}{n_1} + \dfrac{{s_2}^2}{n_2}} } \] 공식을 이용해 \(t\)통계치을 계산한다. 각 요인별 값의 갯수, 평균, 및 표준편차가 필요하다.

df %>% 
  summarise.(n = n(),
             mean = mean(hours),
             sd = sd(hours),
             .by = college) -> t_df; t_df

## # A tidytable: 2 x 4
##   college       n  mean    sd
##   <fct>     <int> <dbl> <dbl>
## 1 degree      174  42.4  14.4
## 2 no degree   326  40.8  15.0

x1 <- t_df$mean[1]
x2 <- t_df$mean[2]
s1 <- t_df$sd[1]
s2 <- t_df$sd[2]
n1 <- t_df$n[1]
n2 <- t_df$n[2]

(x1 - x2) / sqrt(s1^2/n1 + s2^2/n2)

## [1] 1.11931

아래 함수로도 \(t\)통계치를 구할 수 있다.

obs_t <- df %>%
  specify(hours ~ college) %>%
  hypothesize(null = 'independence') %>%
  calculate(stat = 't', order = c("degree", "no degree"))

그 다음 영가설하에서 발생 가능한 \(t\)통계치의 분포를 구한다.

t_dist <- df %>%
  specify(hours ~ college) %>%
  assume(distribution = 't') 
t_dist %>% visualize()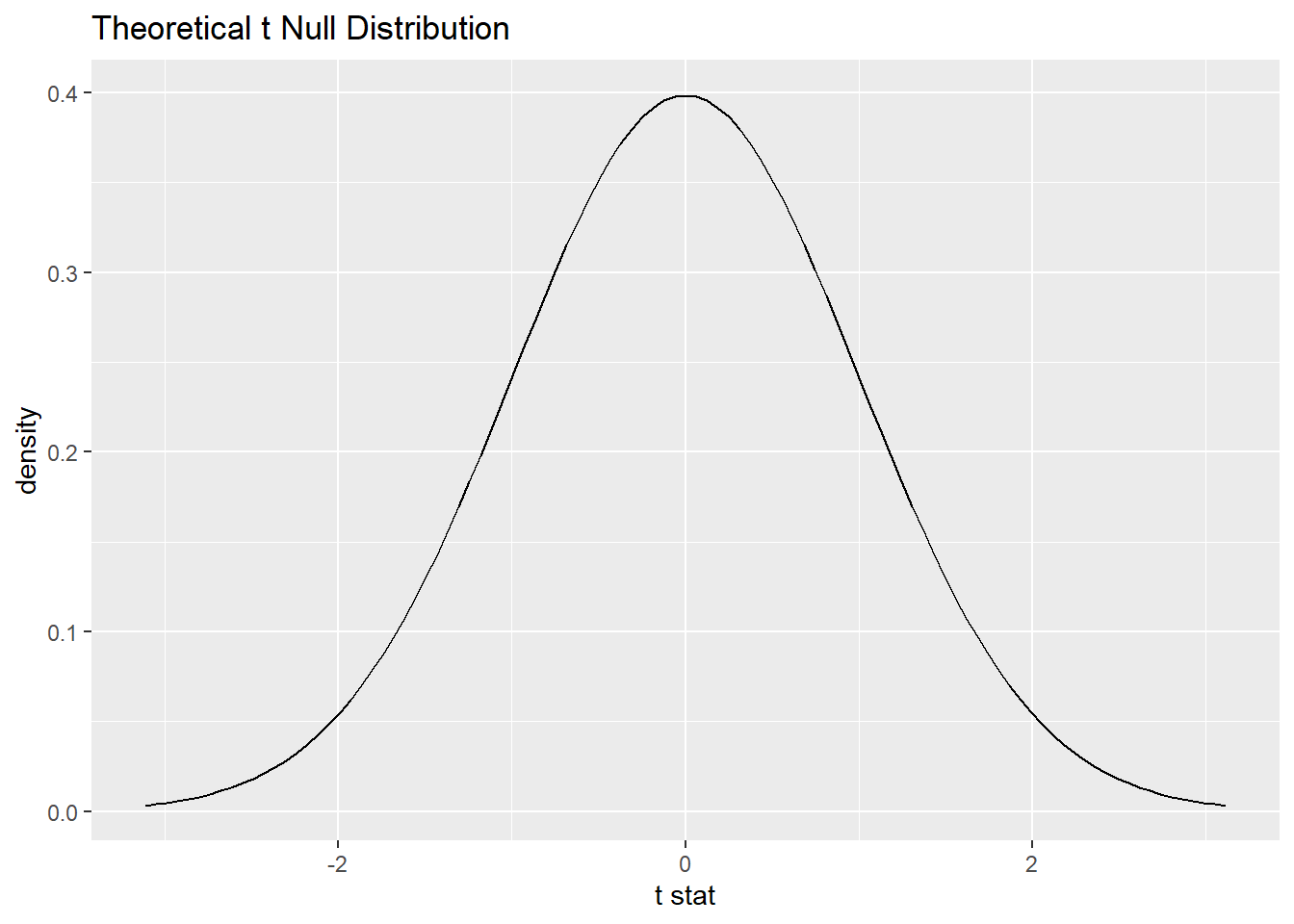

이 분포를 이용해 영가설 하에서 관측한 표본의 \(t\)통계치가 모집단에 실재할 가능성 \(p\)값을 구한다. \(p\)값이 작을수록 영가설하에서 발생가능성이 작다는 의미. 극단적인 사례(즉, 우연이 아닐 가능성)일 가능성이 높다.

p_value_2_sample <- t_dist %>%
  get_p_value(obs_stat = obs_t,
              direction = 'two-sided') %>% pull.()
p_value_2_sample

## [1] 0.2637428

\(p\)값과 함께 분포를 시각화하면 다음과 같다.

t_dist %>% 
  visualize() +
  shade_p_value(obs_stat = obs_t, 
                direction = 'two-sided')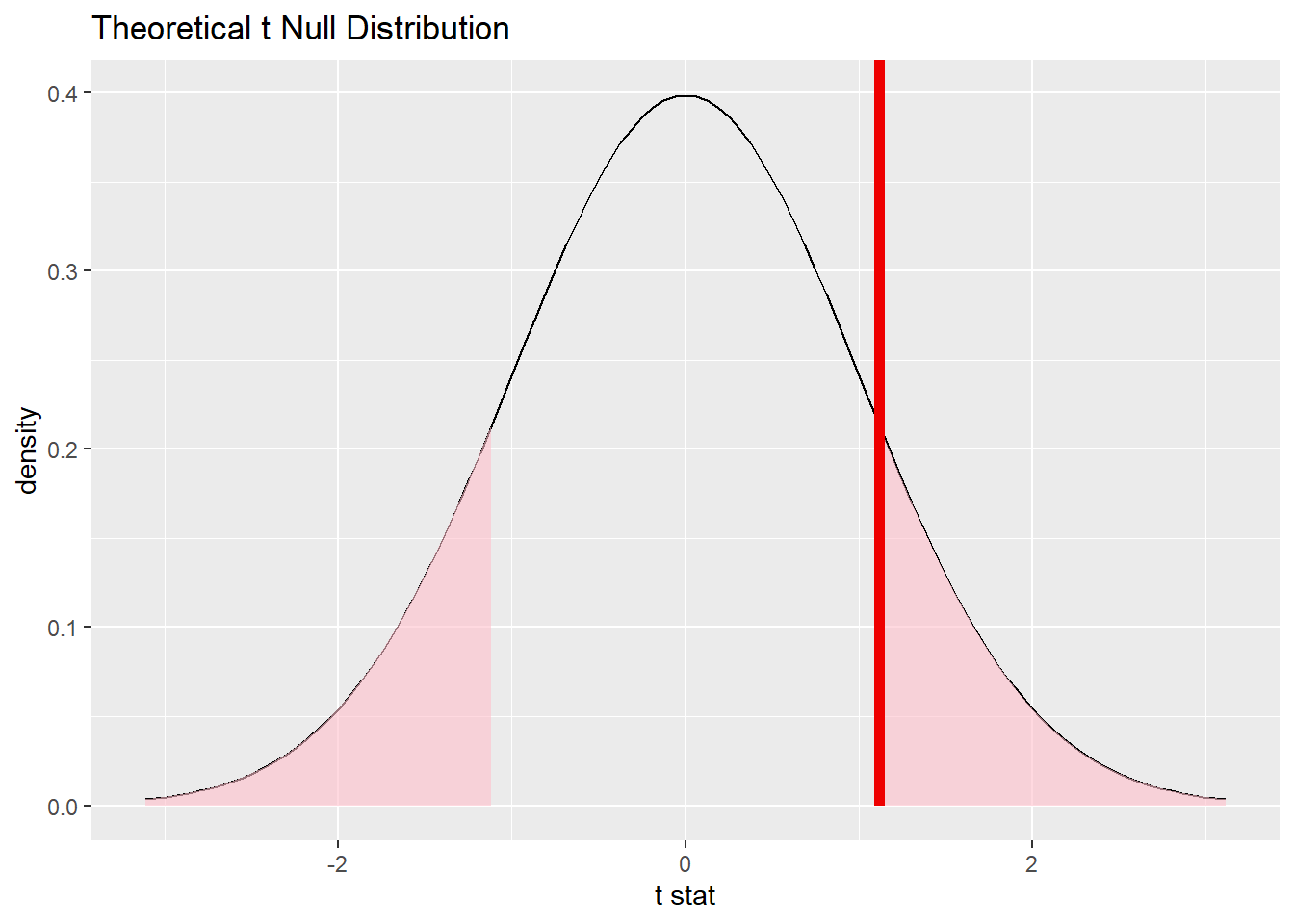

\(p\)값 0.26가 통상적인 유의수준 0.05보다 크기 때문에, \(t\)통계치 1.12가 극단적인 값일 가능성은 낮다. 따라서 영가설을 기각하지 않고 유지한다.

결국 gss자료에 따르면, 대학학위 유무와 노동시간 사이에는 통계적으로 유의한 차이가 없다는 판단을 할 수 있다.

이론 기반 \(t\)검정은 t_test()함수나 t.test()함수로도 할수 있다.

df %>% t_test(
  formula = hours ~ college,
  order = c("degree", "no degree"),
  alternative = "two-sided"
) %>%
  gt() %>%
  tab_header("대학학위유무와 노동시간 관계: 이론접근") %>%
  fmt_number(c(1, 2, 5:7), decimals = 2) %>%
  fmt_number(3, decimals = 3)

대학학위유무와 노동시간 관계: 이론접근
statistic	t_df	p_value	alternative	estimate	lower_ci	upper_ci
1.12	365.64	0.264	two.sided	1.54	−1.16	4.24

statistic: \(t\)통계치
estimate: 집단간 평균 차이

8.1.2 시뮬레이션 기반 가설검정

시뮬레이션기반 가설검정에서는 표본을 반복적으로 재표집(resampling)해 복수(5000 ~ 10000개 권장)의 하위표본(subsample)을 만들어, 표본평균의 분포를 구성해 \(p\)값을 계산한다.

복원추출을 통한 재표집을 부트스트래핑(bootstrapping) 재표집, 비복원추출을 통한 퍼뮤테이션(순열: permutation) 재표집이라고 한다.

즉, 이론기반 가설검정에서는 표본을 하나만 표집해 공식에 따라 통계치를 계산해 \(p\)값을 구하는 반면, 시뮬레이션기반 가설검정에서는 공식에 의지하지 않고 무수히 많은 통계치를 통해 \(p\)값을 구한다 (Figure 8.1).

아래 도표에 시뮬레이션 기반 가설검정의 원리가 잘 나타나 있다.

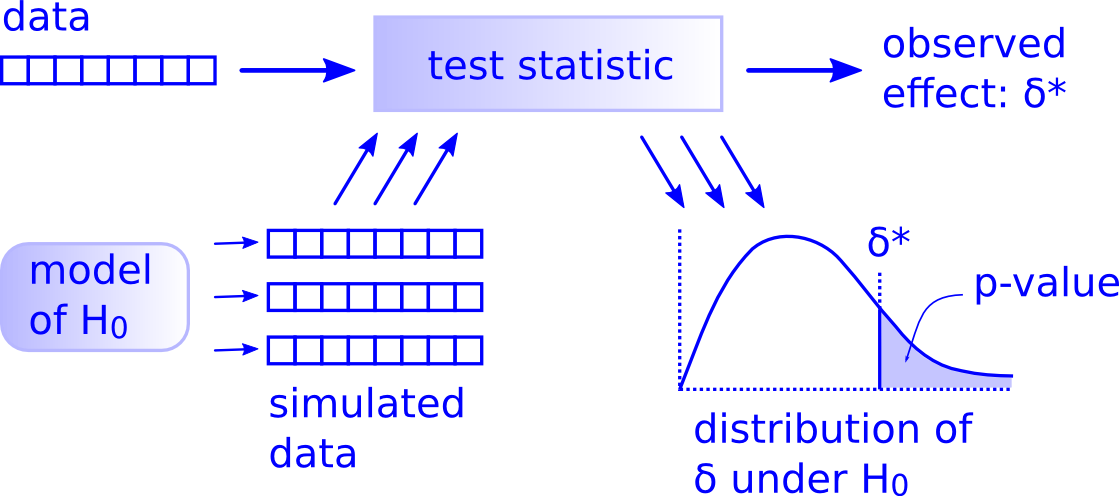
Figure 8.1: 시뮬레이션기반 가설검정

먼저, 10개만 재표집(순열)해 표본분포를 만들어 보자.

null_dist_sim <- df %>% 
  specify(hours ~ college) %>% 
  hypothesize(null = 'independence') %>% 
  generate(reps = 10, type = 'permute') %>% 
  calculate(stat = 'diff in means', 
            order = c("degree", "no degree")) 
null_dist_sim

## Response: hours (numeric)
## Explanatory: college (factor)
## Null Hypothesis: independence
## # A tibble: 10 x 2
##    replicate   stat
##        <int>  <dbl>
##  1         1  1.14 
##  2         2  1.07 
##  3         3  4.12 
##  4         4  0.842
##  5         5  0.419
##  6         6  0.234
##  7         7 -0.762
##  8         8 -1.78 
##  9         9 -1.92 
## 10        10 -0.850

이 결과를 시각화하면 다음과 같다.

observed_statistic <- df %>% 
  specify(hours ~ college) %>% 
  calculate(stat = 'diff in means', 
            order = c("degree", "no degree"))
round(observed_statistic, 2)

## Response: hours (numeric)
## Explanatory: college (factor)
## # A tibble: 1 x 1
##    stat
##   <dbl>
## 1  1.54

null_dist_sim %>% 
  visualise() + 
  shade_p_value(observed_statistic,
                direction = 'greater')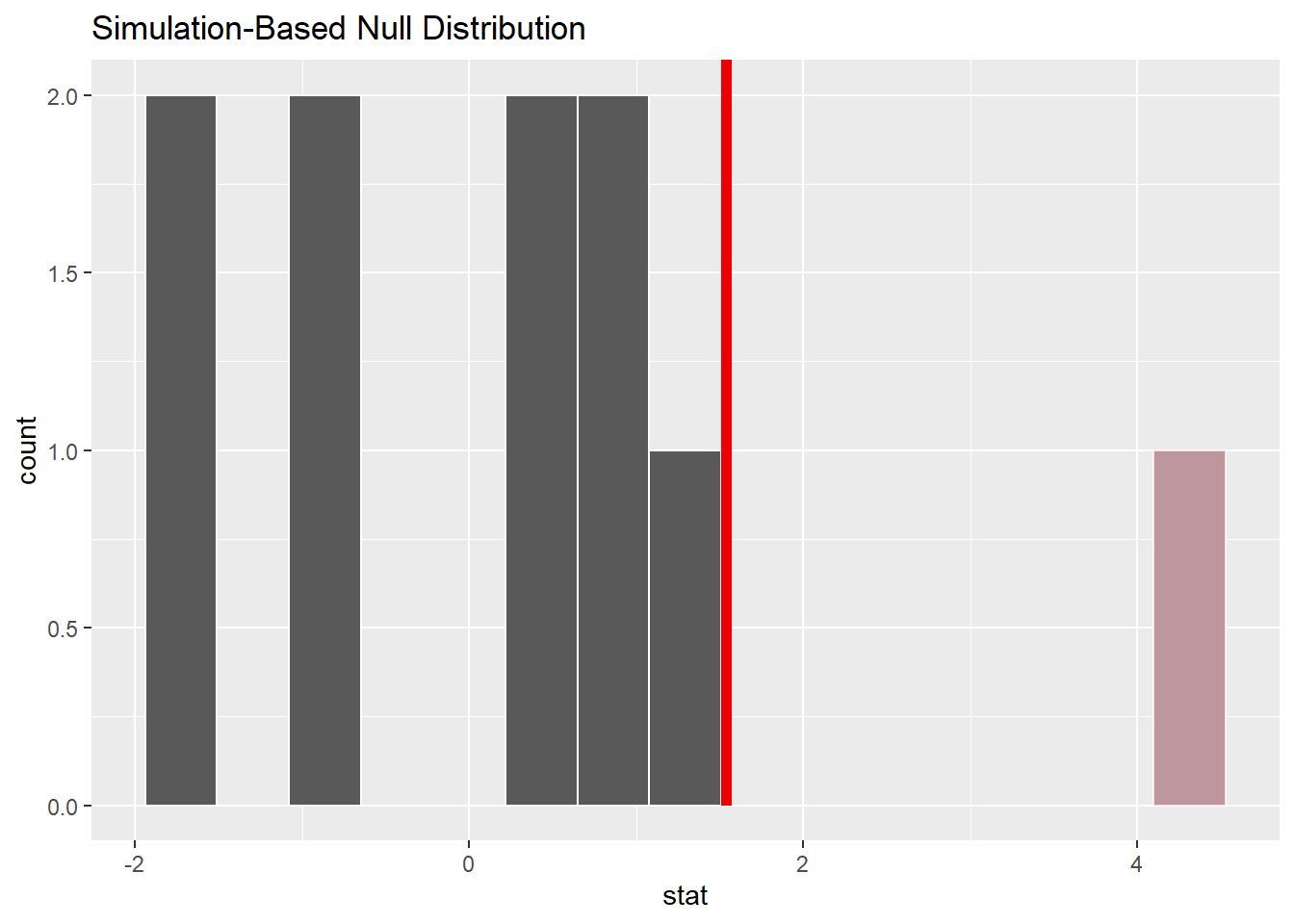

재표집 표본을 1000개로 늘려보자. 표본분포가 정규분포를 이룬다.

set.seed(37)
df %>% 
  specify(hours ~ college) %>% 
  hypothesize(null = 'independence') %>% 
  generate(reps = 1000, type = 'permute') %>% 
  calculate(stat = 'diff in means', 
            order = c("degree", "no degree")) %>% 
  visualise() + 
  shade_p_value(observed_statistic,
                direction = 'two-sided')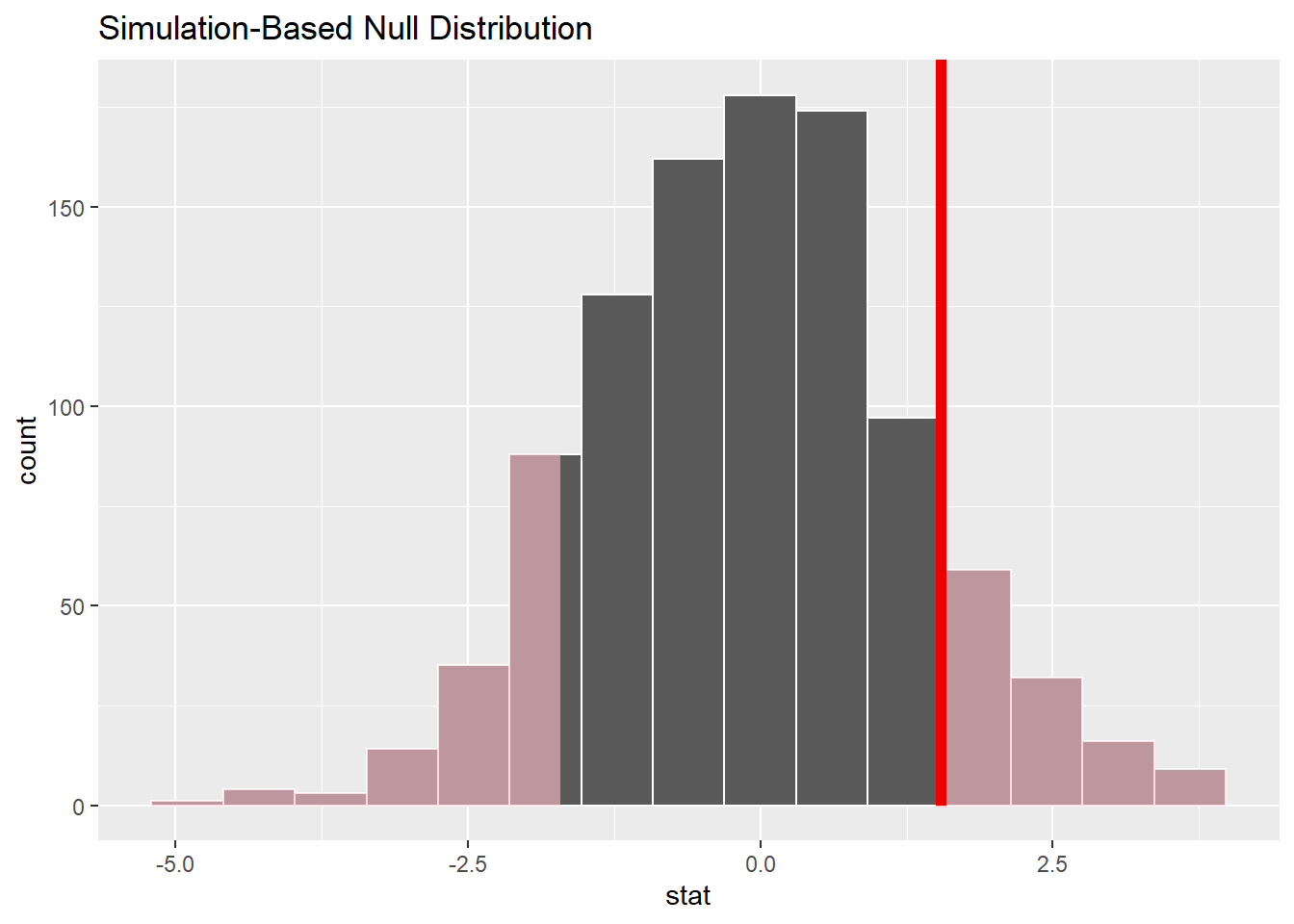

8.1.2.1 유의확률(유의도)

영가설(모평균의 차이가 0)하에서, 관측한 평균의 차이 1.54시간은 발생가능성이 적지는 않아 보인다. 이 관측값과 표본분포로 \(p\)값(유의도/유의확률)을 구하면 다음과 같다.

p_value_2_sample <- null_dist_sim %>%
  get_p_value(obs_stat = observed_statistic,
              direction = 'two-sided') %>% pull.()
p_value_2_sample

## [1] 0.2

\(p\)값이 0.2이므로, 모집단에서 대학학위 유무와 노동시간 사이에 차이가 없다면, 관측한 표본평균의 차이 1.54보다 더 극단적인 통계치를 구할 확률은 약 0.2이다.

유의수준을 0.05로 설정한다면, 영가설을 기각하지 않고 유지한다.

그런데, 0.2은 이론기반 가설검정에서 구한 \(p\)값 0.26과는 많이 다르다. 재표집 회수가 충분하지 않기 때문이다. 재표집 회수를 5000회로 늘려보자. 이론기반 재표집 결과와 비슷해진다.

set.seed(37)
df %>% 
  specify(hours ~ college) %>% 
  hypothesize(null = 'independence') %>% 
  generate(reps = 5000, type = 'permute') %>% 
  calculate(stat = 'diff in means', 
            order = c("degree", "no degree")) %>% 
  get_p_value(observed_statistic,
                direction = 'two-sided')

## # A tibble: 1 x 1
##   p_value
##     <dbl>
## 1   0.278

set.seed(37)
df %>% 
  specify(hours ~ college) %>% 
  hypothesize(null = 'independence') %>% 
  generate(reps = 5000, type = 'permute') %>% 
  calculate(stat = 'diff in means', 
            order = c("degree", "no degree")) %>% 
  get_p_value(observed_statistic,
                direction = 'two-sided')

## # A tibble: 1 x 1
##   p_value
##     <dbl>
## 1   0.278

8.1.2.2 신뢰구간

infer패키지를 이용한 신뢰구간은 다음과 같다. 유의성 검정과 기본적인 구조는 같다.

boot_dist <- df %>% 
  specify(hours ~ college) %>% 
  # hypothesize() 없이 다음 단계
  # 'permute'대신 'bootstrap' 사용
  generate(reps = 1000, type = 'bootstrap') %>% 
  calculate(stat = 'diff in means', 
            order = c("degree", "no degree"))

표본분포를 생성했으면, 신뢰구간을 구한다.

percentile_ci <- boot_dist %>% 
  get_confidence_interval(level = 0.95, 
                          type = 'percentile')
percentile_ci

## # A tibble: 1 x 2
##   lower_ci upper_ci
##      <dbl>    <dbl>
## 1    -1.11     4.14

표본평균의 차이는 95% 신뢰수준 -1.11과 4.14사이에 있다. 즉, 100번 중 95번은 모집단에서 비교집단(대학학위 유 vs. 무)의 차이가 [-1.11, 4.14]사이에 있다.

신뢰구간을 부트스트랩표본 분포로 시각화하면 다음과 같다.

boot_dist %>% 
  visualize() +
  shade_ci(endpoints = percentile_ci)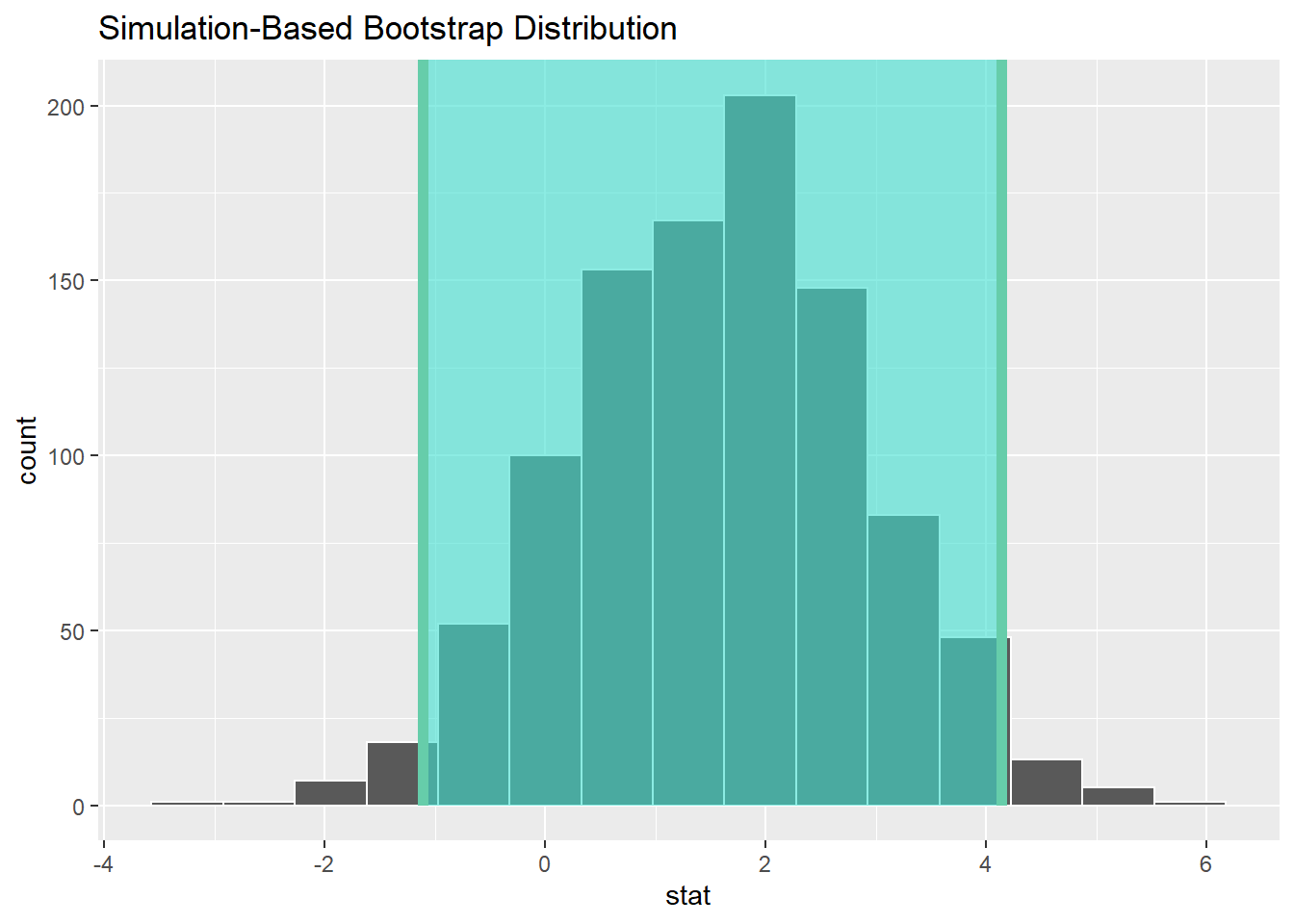

집단간 평균값의 차이에 대한 95% 신뢰구간내에 0이 포함돼 있으므로, 집단간 차이는 95% 수준에서 음성이라고 판단할 수 있다.

infer패키지를 이용한 시뮬레이션 기반 가설검정은 이론기반 검정에 비해 복잡해 보인다. 그렇다면, 더 간단한 이론기반 가설검정을 두고 복잡한 시뮬레이션기반 가설검정을 하는 이유는 무엇일까?

우선, 재표집 회수가 충분하면 시뮬레이션기반 가설검정의 결정오류 가능성이 줄기 때문이다. 특히, 표본 값의 분포가 정규분포가 아닐때 그러하다.

둘째, infer패키지의 가설검정 구조가 가설검정의 절차를 그대로 구현한다는데 있다.

specify(): 데이터프레임에서 관심 변수 지정
hypothesize(): 영가설 설정
generate(): 재표집해 영가설이 참인 경우의 표본분포 생성.
calculate(): 필요한 통계치 계산
visualsize(): 영가설분포를 만들어 관측한 검정통계치를 비교해 \(p\)값 계산.

이런 가설검정의 구조는 \(t\)검정뿐 아니라, \(F\)검정, 상관분석 및 회귀분석 등 거의 모든 통계추론에 적용할 수 있다.

8.1.3 정리

8.1.3.1 `infer`패키지의 \(p\)값을 이용한 영가설유의성검정 방법

영가설하의 표본분포 계산(순열재표집)

null_dist_sim <- data_df %>% 
  specify(DV ~ IV) %>% 
  hypothesize(null = 'independence') %>% 
  generate(reps = 5000, type = 'permute') %>% 
  calculate(stat = 'diff in means', 
            order = c("level1", "level2"))

표본 통계치 계산

observed_statistic <- data_df %>% 
  specify(DV ~ IV) %>% 
  #hypothesize(null = 'independence') %>% 
  #generate(reps = 5000, type = 'permute') %>% 
  calculate(stat = 'diff in means', 
            order = c("level1", "level2"))

\(p\)값 계산

p_value_2_sample <- null_dist_sim %>%
  get_p_value(obs_stat = observed_statistic,
              # 양측검정
              direction = 'two-sided') %>% pull.()
p_value_2_sample

영가설하 표본분포에 \(p\)값 표시

null_dist_sim %>% 
  visualise() + 
  shade_p_value(observed_statistic,
                direction = 'two-sided')

8.1.3.2 신뢰구간을 이용한 가설검정 방법

영가설하의 표본분포 계산(부트스트랩재표집)

boot_dist <- data_df %>% 
  specify(DV ~ IV) %>% 
  hypothesize(null = 'independence') %>% 
  generate(reps = 5000, type = 'bootstrap') %>% 
  calculate(stat = 'diff in means', 
            order = c("level1", "level2"))

표본 통계치 계산

boot_dist <- data_df %>% 
  specify(DV ~ IV) %>% 
  #hypothesize(null = 'independence') %>% 
  #generate(reps = 5000, type = 'bootstrap') %>% 
  calculate(stat = 'diff in means', 
            order = c("level1", "level2"))

신뢰구간 계산

percentile_ci <- boot_dist %>% 
  get_confidence_interval(level = 0.95, 
                          type = 'percentile')
percentile_ci

영가설하 표본분포에 신뢰구간 표시

boot_dist %>% 
  visualize() +
  shade_ci(endpoints = percentile_ci)

8.1.4 t검정 결과 보고방법

분석결과를 다른 사람과 공식적으로 공유할 때는 일정한 형식을 지켜야 한다. 무엇을 어떻게 분석했는지 그 결과가 무엇인지, 그리고 그 결과의 의미가 무엇인지 들을 일관되게 나타내야 하기 때문이다. \(t\)검정을 한 경우 다음과 같은 방식으로 분석결과를 보고한다.

기술통계치: 관측개수, 평균, 표준편차

df %>% summarise.(
  n = n(hours),
  m = mean(hours),
  sd = sd(hours), 
  .by = college) -> des_df
des_df %>% gt() %>% 
  tab_header("대학학위 유무별 노동시간 기술통계") %>% 
  fmt_number(3:4, decimals = 2)

대학학위 유무별 노동시간 기술통계
college	n	m	sd
degree	174	42.39	14.43
no degree	326	40.85	15.02

추론통계치: \(t\)통계치, \(p\)값, 신뢰구간

df %>% t_test(
  formula = hours ~ college,
  order = c("degree", "no degree"),
  alternative = "two-sided") -> inf_df
inf_df %>% gt() %>% 
  tab_header("대학학위유무와 노동시간 관계") %>%
  fmt_number(c(1, 2, 5:7), decimals = 2) %>%
  fmt_number(3, decimals = 3)

대학학위유무와 노동시간 관계
statistic	t_df	p_value	alternative	estimate	lower_ci	upper_ci
1.12	365.64	0.264	two.sided	1.54	−1.16	4.24

위와 같은 분석결과에 대해 다음과 같이 기술한다.

대학학위 보유자(n = 174)의 노동시간(\(M\) = 42.39, \(SD\) = 14.43)과 대학학위 미보유자(n = 326)의 노동시간(\(M\) = 40.85, \(SD\) = 15.02) 사이의 차이는 통계적으로 유의하지 않다, \(t\) = 1.12, \(p\) = 0.264, 95%CI[-1.16, 4.24].

또한 이 결과는 아래와 같이 도표로 시각화해 보고한다.

# 평균과 표준편차 표시하기 위해 데이터프레임에 값 포함
df %>% mutate.(
  m = mean(hours) %>% round(2), 
  sd = sd(hours) %>% round(2),
  .by = college) %>% 
# 도표  
ggplot(aes(x = college, y = hours, 
                 color = college)) +
  # ggforce패키지로 시나플롯 
  ggforce::geom_sina(alpha = .3) +
  # 표준편차로 에러바 표시
  geom_errorbar(aes(x = college, y = m,
                    ymin = m - sd, ymax = m + sd),
                width = .2, color = 'dimgray') +
  # 평균 점으로 표시
  geom_point(aes(x = college, y = m), 
             color = 'dimgray', size = 3) +
  # 평균 텍스트로 표시
  geom_text(stat = 'summary',
            aes(label = paste("M:", round(..y.., 2))),
            color = 'black', size = 4, nudge_x = .18) +
  # ggpubr패키지로 p값 표시
  ggpubr::stat_compare_means(
    method = 't.test', vjust = 3, hjust = -.5) + 
  labs(title = "대학학위유무별 노동시간 차이",
       caption = "Note: M = 평균",
       x = "대학학위 유무",
       y = "주당 노동시간") + 
  theme(legend.position = 'none') +
  ylim(0, 100)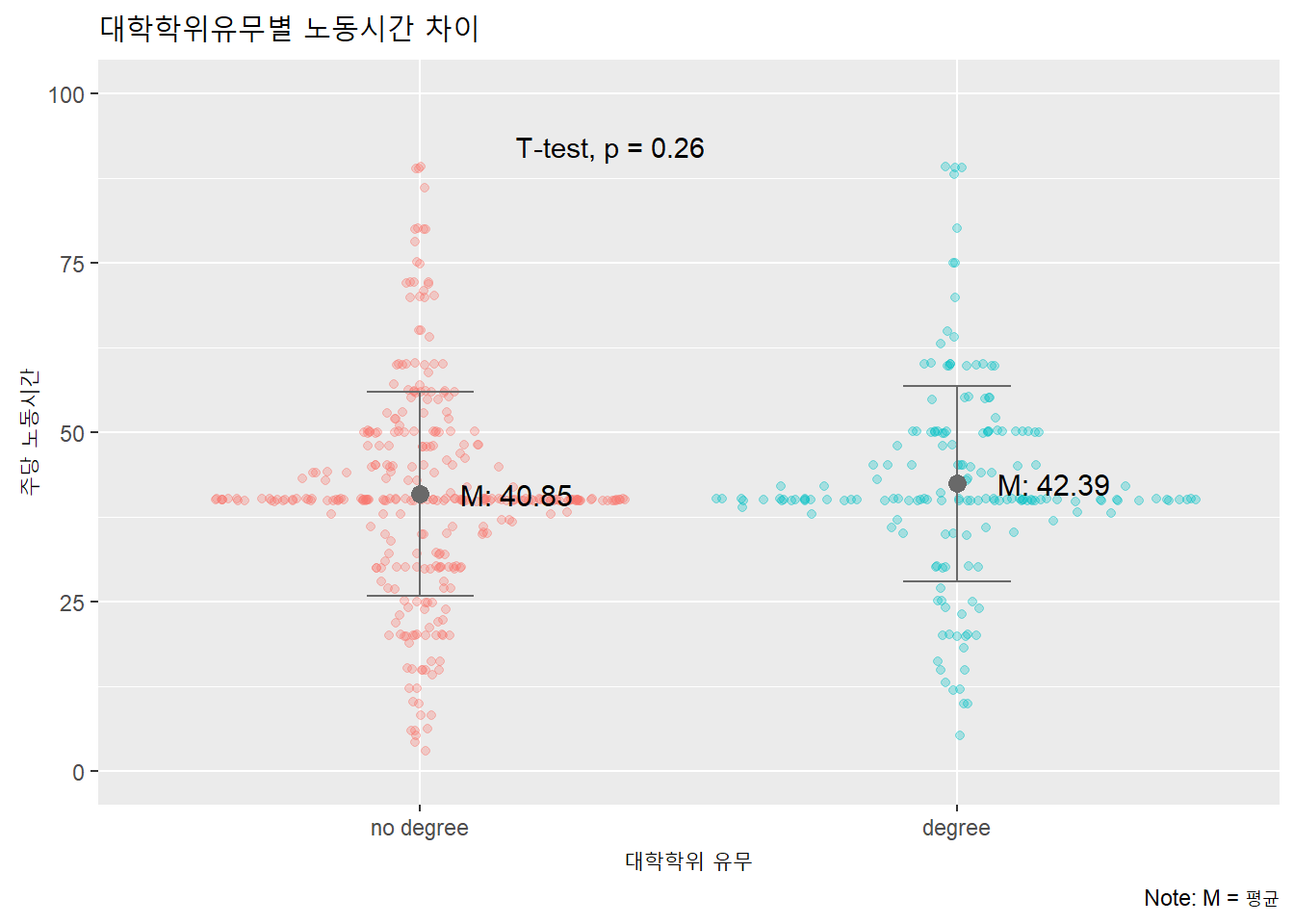

8.2 분산분석

8.2.1 일원분산분석

t검정은 두 집단의 평균의 차이를 비교하는데 사용할수 있다. 단일 표본을 모집단과 비교하거나(일표본 t검정), 단일 표본의 사전-사후 평균을 비교하거나(짝진 t검정), 혹은 독립된 두 표본의 평균을 비교한다(이표본 t검정).

비교할 대상이 3개 이상인 경우는 어떻게 해야할까?

예를 들어, 미국 일반사회조사(GSS) 자료에서 계층(class)은 비교할 집단 4개인 범주형 자료다.

gss %>% select.(hours, class) -> df
summary(df)

##      hours                 class    
##  Min.   : 3.00   lower class  : 20  
##  1st Qu.:36.75   working class:251  
##  Median :40.00   middle class :209  
##  Mean   :41.38   upper class  : 20  
##  3rd Qu.:48.00   no class     :  0  
##  Max.   :89.00   DK           :  0

이처럼 3개 이상의 집단간 차이를 비교해야 하는 상황에서 집단을 2개씩 짝(lower - working, lower - middle, lower - upper, …)을 지어 여러 차례 비교하면 1종오류 가능성이 올라간다.

유의수준 0.05에서 1종오류 발생 가능성
- 가설검정 1회: 100% - 95% = 5%
- 가설검정 2회: 100% - (95% * 95% = 90.25%) = 9.75%
- 가설검정 3회: 100% - (95% * 95% * 95% = 85.74%) = 14.26%

비교할 집단이 3개 이상일 때 활용할 수 있는 분석방법이 분산분석( = 변량분석: ANOVA)이다.

ANOVA : ANalysis Of VAriance
분산(variance): 자료의 값이 평균으로부터 퍼져있는 정도

가변수(dummy variable)를 이용한 회귀분석도 3개 이상의 집단간 차이를 비교하는데 사용할 수 있다.

분산분석의 영가설은 모든 연구 집단의 평균이 같다.

\(H_0\): \(\mu_1\) = \(\mu_2\) = \(\mu_3\) … = \(\mu_k\)

따라서, 분산분석에서 영가설은 최소한 한 집단의 평균이 나머지 집단의 평균과 다르면 기각한다.

여러 집단의 평균을 동시에 비교하기 위해서 활용하는 값이 집단간 분산(Between Groups Variance)의 정도다. 집단 사이의 분산의 정도가 크면, 집단간 평균의 차이가 있는 집단이 최소한 하나는 있다는 지표가 된다.

집단간분산만으로는 집단간 차이를 나타낼 수 없다. 오차(error)인 집단내 분산(Within Group Variance)을 고려해야 하기 때문이다. 집단내 분산의 정도가 크면, 집단간 평균의 차이가 크지 않아도 집단간 분산이 큰것처럼 보일 수 있다.

집단간 평균의 차이는 집단간분산을 집단내분산으로 나눈값으로 구하게 된다.

집단간 분산의 정도 대비 집단내 분산(잔차: residual)의 정도로 집단간 차이를 판단하기 때문에 분산분석이라고 한다. 집단간 차이에 대해 집단내 분산은 오차(error)에 해당하기 때문에 집단내 분산을 잔차(residual)이라고도 한다.

\[ F = \frac{집단간 분산(BetweenGroups Variance)}{집단내 분산(WithinGroup Variance)} \] 집단간 분산은 MSG(mean square between groups)로 나타내고, 집단내 분산은 MSE(mean square error)로 나타낸다.

\[ F = \frac{MeanSquareBetweenGroups(MSG)}{MeanSquareError(MSE)} \] 집단간 분산과 집단내 분산이 같다면, \(F\)값은 1이 된다. \(F\)값이 1보다 크면 두 집단 사이에 차이가 있다고 판단할 수 있다.

\(F\)통계치를 이용하기 때문에 분산분석을 \(F\)검정이라고도 한다.

일원분산분석(one-way ANOVA)은 요인(factor)이 하나인 분산분석이다. 요인은 집단을 구분하는 독립변수다. 각 집단은 요인의 수준(level)이다. GSS자료에서 class는 요인(독립변수)이고, lower class, working class 등의 집단이 요인의 수준이다.

집단간 차이를 비교하는 분석이므로 독립변수는 범주형이고, 종속변수는 연속형이다.
요인이 n개인 분산분석은 다원분산분석(n-way ANOVA)이다.

GSS자료에서 계층(class)별 노동시간의 차이를 분석해보자. 먼저, 편의를 위해 class변수의 각 수준에서 ’class’를 제거해 단일 단어로 바꾼다.

df$class %>% unique()

## [1] middle class  working class lower class   upper class  
## Levels: lower class working class middle class upper class no class DK

df %>% mutate.(
  class = str_remove_all(class, pattern = " class") %>% 
    factor(
      levels = c("lower", "working", "middle", "upper")
      )) -> df
summary(df)

##      hours           class    
##  Min.   : 3.00   lower  : 20  
##  1st Qu.:36.75   working:251  
##  Median :40.00   middle :209  
##  Mean   :41.38   upper  : 20  
##  3rd Qu.:48.00                
##  Max.   :89.00

추론분석을 하기 전에는 늘 기술통계와 시각화 등 탐색분석을 먼저 수행한다. 노동시간(hours)에 대한 각 집단(class열의 4개 요인)별 평균을 분포화 함께 시각화해보자.

psych::describe(df)

##        vars   n  mean    sd median trimmed  mad min max range skew kurtosis
## hours     1 500 41.38 14.82     40   41.02 7.41   3  89    86 0.41     1.41
## class*    2 500  2.46  0.64      2    2.45 0.00   1   4     3 0.16    -0.22
##          se
## hours  0.66
## class* 0.03

df %>% 
  mutate.(
    m = mean(hours), sd = sd(hours), .by = class
  ) %>% 
  ggplot(aes(class, hours, color = class)) +
  geom_sina(alpha = 0.5) +
  geom_errorbar(
    aes(x = class, y = m, ymin = m - sd, ymax = m + sd),
    color = 'dimgray', width = .2) +  
  geom_point(
    aes(x = class, y = m), 
    color = 'dimgray', size = 3) +
  geom_text(stat = 'summary',
            # ..y.. 내부 변수 
            aes(label = paste("M:", round(..y.., 2))),
            color = 'black', size = 4, nudge_x = .3) +
  labs(title = "계층별 노동시간 평균과 분포",
       x = "계층",
       y = "주당 노동시간") + 
  theme(legend.position = 'none')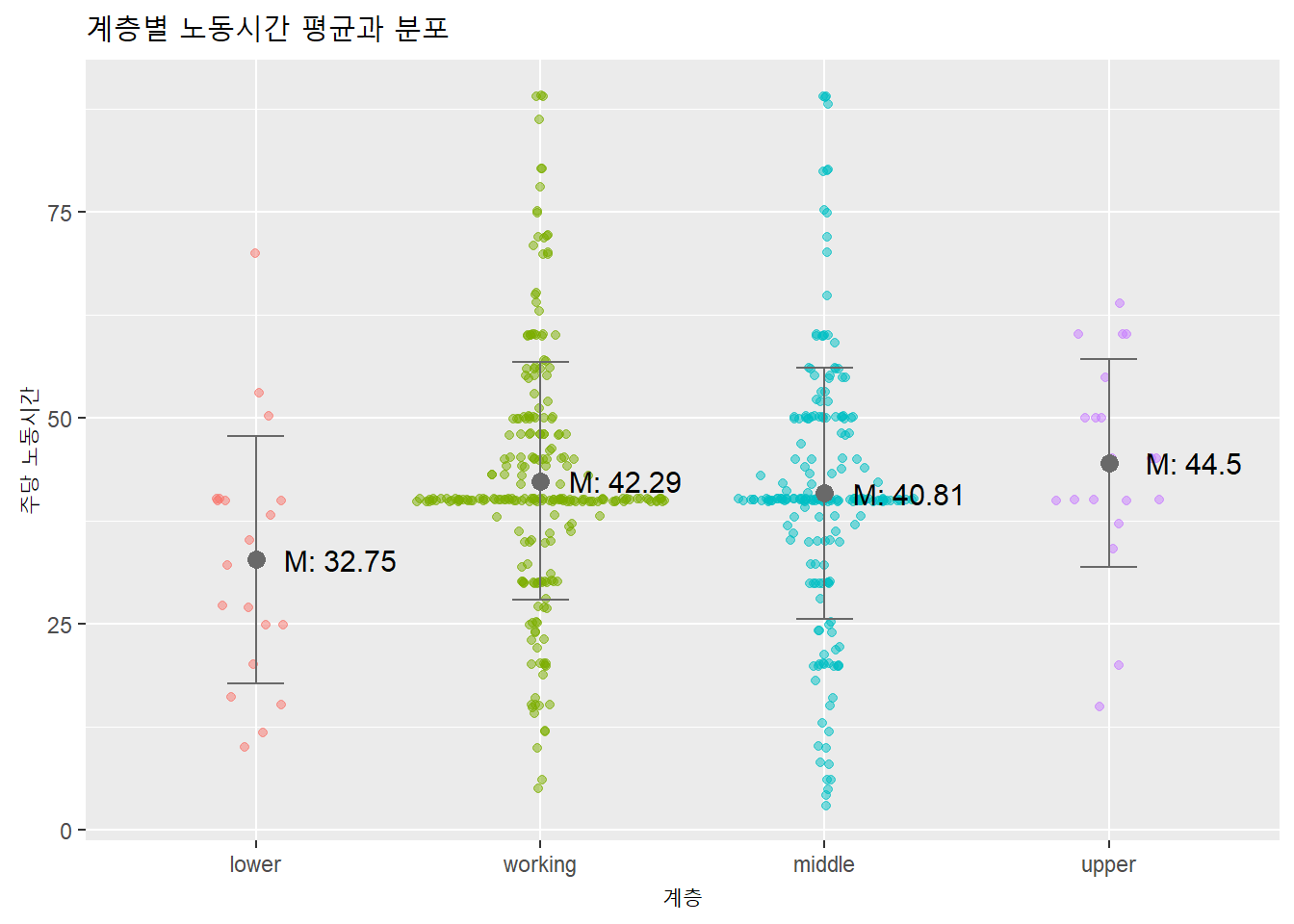

시뮬레이션 기반 분산분석을 먼저 하자. 먼저 표본분포를 만든다. 순열재표집을 1000회 시행.

f_dist <- df %>% 
  specify(hours ~ class) %>% 
  hypothesise(null = 'independence') %>% 
  generate(reps = 1000, type = 'permute') %>% 
  # F검정이므로 F투입
  calculate(stat = 'F')

\(p\)값을 계산하고, 이를 영가설하에서의 표본분포에 표시하자.

# F통계치 계산
f_stat <- df %>% 
  specify(hours ~ class) %>% 
  calculate(stat = 'F')
f_stat

## Response: hours (numeric)
## Explanatory: class (factor)
## # A tibble: 1 x 1
##    stat
##   <dbl>
## 1  3.01

# p값 계산 F검정은 단측검정
f_dist %>% 
  get_p_value(f_stat, direction = 'greater') -> p_fstat
p_fstat

## # A tibble: 1 x 1
##   p_value
##     <dbl>
## 1   0.029

# 표본분포에 p값 표시
f_dist %>% 
  visualise() +
  shade_p_value(f_stat, direction = 'greater')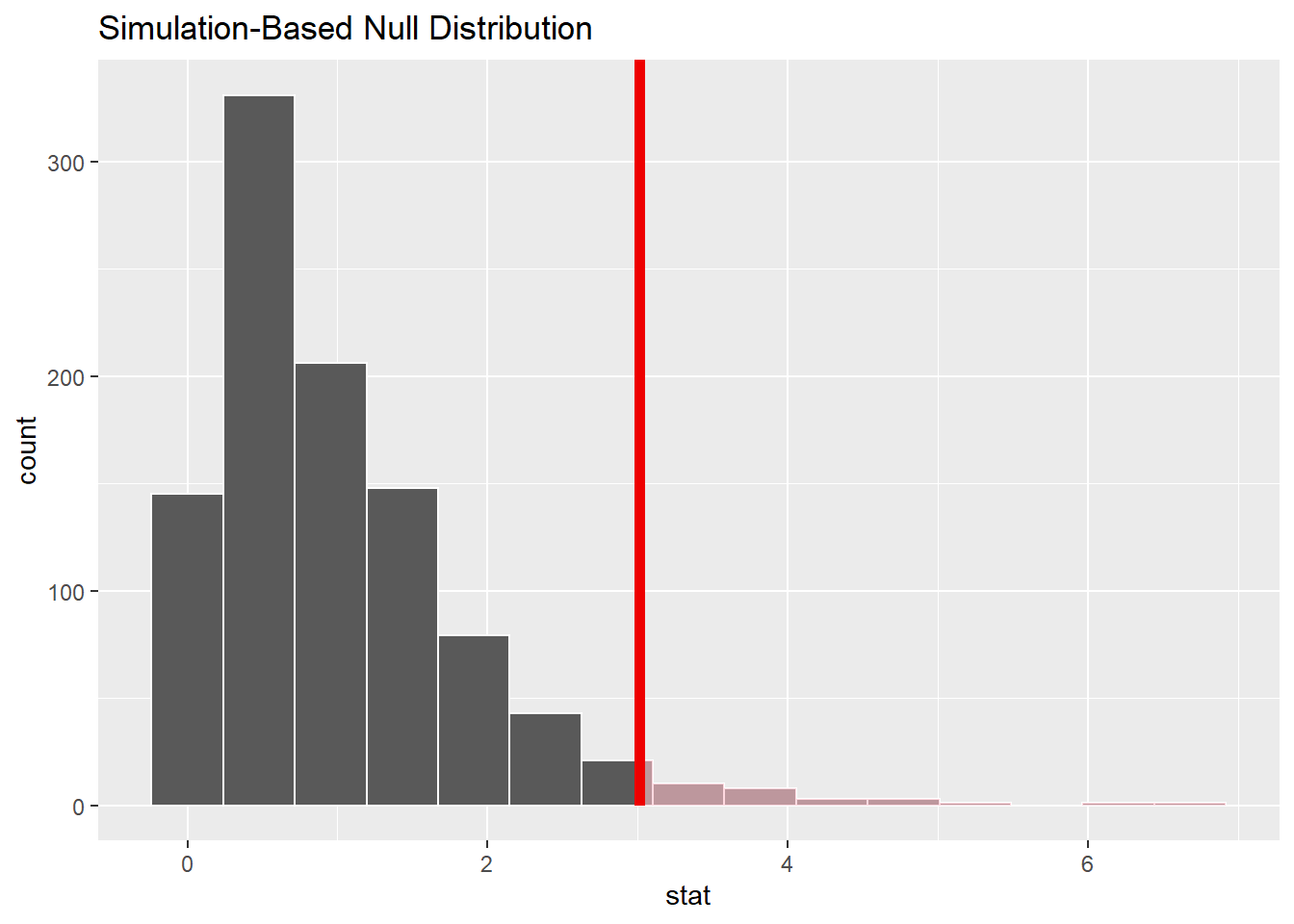

이론적인 영가설하의 분포를 함께 표시하려면 method = 'both'인자를 이용한다.

f_dist %>% 
  visualise(method = 'both') +
  shade_p_value(f_stat, direction = 'greater')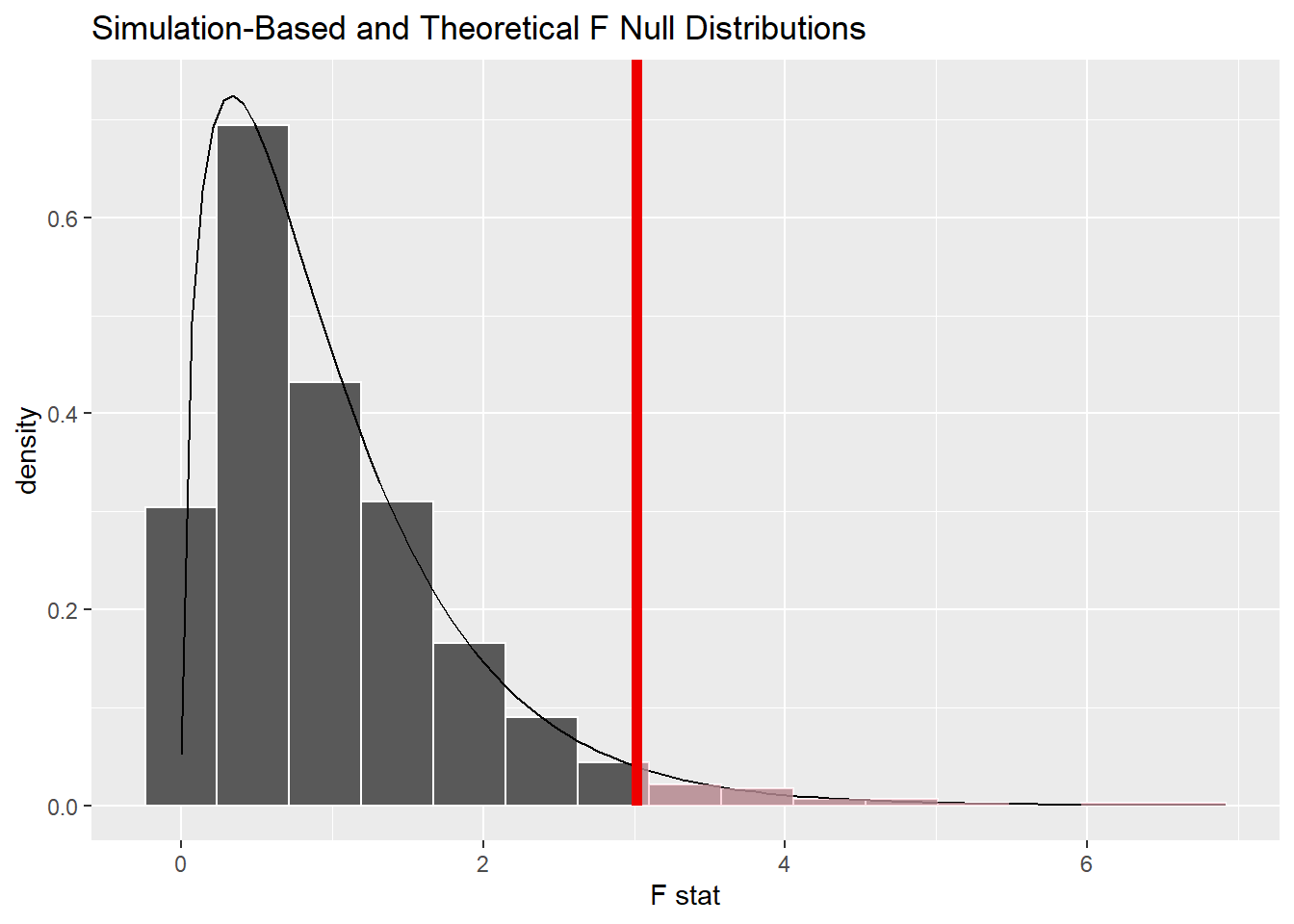

\(p\)값이 0.03으로 유의수준 0.05보다 작기 때문에, 관측된 통계치는 영가설하에서 발생하기에는 극단적인 사례라 판단한다. 따라서, 영가설 기각하고 대립가설 채택한다.

aov()함수를 이용한 분산분석 결과는 다음과 같다.

df %>% aov(hours ~ class, .) %>% tidy() %>% 
  gt() %>% 
  tab_header("계층별 노동시간의 관계: 분산분석") %>% 
  fmt_number(-c(1:2), decimals = 2) %>% 
  fmt_number(p.value, decimals = 3)

계층별 노동시간의 관계: 분산분석
term	df	sumsq	meansq	statistic	p.value
class	3	1,961.38	653.79	3.01	0.030
Residuals	496	107,634.66	217.01	NA	NA

class 행의 meansq: 집단간 분산
Residuals 행 meansq: 집단내 분산
statistic: \(F\)통계치
df: 자유도(degree of freedom)

분산분석의 자유도는 2종이 있다.

집단간 분산의 자유도: class행의 df열(집단 갯수 - 1)
집단내 분산의 자유도: Residual행의 df열(표본 갯수 - 집단 갯수)

집단간분산(class행의 meansq)를 집단내분산(Residuals행의 meansq)로 나누면 \(F\)통계치가 나온다.

df %>% aov(hours ~ class, .) %>% tidy() -> fit_tidy
fit_tidy$meansq[1] / fit_tidy$meansq[2]

## [1] 3.012802

8.2.2 사후분석

분산분석에서 영가설을 기각하고 대립가설을 채택하면, 집단간 평균의 차이가 유의하다고 판단할 수 있다. 그러나, 이는 집단간 평균의 차이가 있다는 것만을 나타낼 뿐이다. 구체적으로 어느 집단(수준) 사이에 평균의 차이가 있는지는 알 수 없다.

분산분석을 통해 통계적으로 유의한 차이를 확인한 다음에는 사후검정(post-hoc test)을 추가로 실시해 어느 집단사이에 차이가 있는지 확인한다.

많이 쓰이는 사후분석 방법은 Tukey의 HSD와 봉페르니 교정(Bonferroni correction)이다.

앞의 분석결과를 통해 사후분석을 해보자.

df %>% aov(hours ~ class, .) %>% TukeyHSD()

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = hours ~ class, data = .)
## 
## $class
##                     diff        lwr       upr     p adj
## working-lower   9.544821  0.7219337 18.367708 0.0280543
## middle-lower    8.063397 -0.8246742 16.951468 0.0908093
## upper-lower    11.750000 -0.2582005 23.758201 0.0577379
## middle-working -1.481424 -5.0373015  2.074454 0.7056163
## upper-working   2.205179 -6.6177077 11.028066 0.9175206
## upper-middle    3.686603 -5.2014685 12.574674 0.7084760

upper집단과 working집단의 노동시간 차이 2.21에 대한 유의확률(\(p\)값)은 0.917로서 통계적으로 유의하지 않다. 영가설이 참일 경우, 두 집단간 평균의 차이가 0일 가능성이 91.7%의 확률이다. 달리 말해, 2.21의 차이는 표본의 차이일뿐 모집단에 실재하는 차이가 아닐 가능성이 높다.
working집단과 lower집단의 노동시간 차이 9.54에 대한 \(p\)값은 0.028이다. 영가설이 참일 경우, 두 집단간 평균의 차이가 0일 가능성이 2.8%의 확률이다. 달리 말해 표본에서 관측된 9.54의 차이는 모집단에 실재하는 차이일 가능성이 높다.
upper집단과 lower집단의 노동시간 차이 11.75에 대한 \(p\)값은 0.057이다. 영가설이 참일 경우, 두 집단간 평균의 차이가 0일 가능성이 5.7%의 확률이다. 달리 말해 표본에서 관측된 11.75의 차이는 모집단에 실재하는 차이가 아닐 가능성이 높다.

8.2.2.1 FWER

사후분석을 하는 또 다른 이유는 1종오류 가능성을 줄이기 위해서다.

FWER(FamilyWise Error Rate)은 하나의 데이터셋으로 수행하는 복수의 가설검정에서, 적어도 하나의 가설에서 1종오류가 발생할 가능성이다.

upper와 lower집단만 따로 추출해 t검정을 해, 사후분석한 결과와 비교해보자.

df %>% filter.(class == "upper" | class == "lower") -> df1
df1 %>% t_test(hours ~ class,
               alternative = 'two-sided')

## # A tibble: 1 x 7
##   statistic  t_df p_value alternative estimate lower_ci upper_ci
##       <dbl> <dbl>   <dbl> <chr>          <dbl>    <dbl>    <dbl>
## 1     -2.68  36.9  0.0110 two.sided      -11.8    -20.6    -2.85

유의확률(\(p\)값)이 0.011로 TukeyHSD 사후분석의 \(p\)값인 0.057보다 작다. 이는 TukeyHSD와 같은 사후분석 방법이 1종오류 가능성을 줄이기 위해 \(p\)값을 보정하기 때문이다.

가설 검정에서 1종오류가 발생하지 않을 가능성은 100%일 수가 없기 때문에, 가설검정의 횟수가 증가할수록 1종오류 발생가능성이 증가한다.

유의수준 0.05에서 1종오류 발생 가능성
- 가설검정 1회: 100% - 95% = 5%
- 가설검정 2회: 100% - (95% * 95% = 90.25%) = 9.75%
- 가설검정 3회: 100% - (95% * 95% * 95% = 85.74%) = 14.26%

집단 2개를 비교하는 경우, 가설검정을 1회만 수행하지만, 비교할 집단의 수가 증가할 수록 비교해야 하는 집단의 수가 증가한다. 따라서, 분산분석으로 집단간 차이가 통계적으로 유의하다는 것이 확인되면, 개별적으로 집단간 t검정을 수행하지 않고, 유의수준을 보정해 FWER을 0.05로 고정하는 사후분석방법을 이용한다.

8.2.3 계획비교

분산분석에 의해 집단간 차이가 통계적으로 유의하다는 결과를 확보한 다음, 유의한 차이가 어느 집단 사이에 있는지 파악하는 방법으로서, 사후적으로 모든 짝에 대하여 분석하는 사후분석과 달리, 계획비교(planned comparison)은 사전에 계획된 짝에 대하여 평균을 비교하는 분석방법이다.

사전에 계획돼 있으므로, 계획비교를 하기 위해서는 연구가설을 통해 비교 대상에 대한 예측이 선행돼야 한다.

계획비교를 하기 위한 방법은 두가지가 있다.

8.2.3.1 가변수

가변수(더미코딩)를 이용한 대비다.

분산분석은 가변수를 이용한 회귀분석과 같다.

df %>% aov(hours ~ class, .) %>% summary.lm()

## 
## Call:
## aov(formula = hours ~ class, data = .)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -37.813  -4.813  -0.813   7.202  48.187 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    32.750      3.294   9.942   <2e-16 ***
## classworking    9.545      3.423   2.789   0.0055 ** 
## classmiddle     8.063      3.448   2.339   0.0198 *  
## classupper     11.750      4.658   2.522   0.0120 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 14.73 on 496 degrees of freedom
## Multiple R-squared:  0.0179, Adjusted R-squared:  0.01196 
## F-statistic: 3.013 on 3 and 496 DF,  p-value: 0.02975

class요인(변수)의 4개 수준이 lower class를 기준으로 대비하도록 설정돼 있다.

levels(df$class)

## [1] "lower"   "working" "middle"  "upper"

만일, lower class를 기준으로 나머지 3개 집단과 각각 짝을 지어 비교하는 것이 사전 계획이라면 이것으로 계획비교가 완료된다.

반면, upper class를 기준으로 나머지 3개 집단과 각각 짝을 지어 비교하는 것이 사전 계획이라면 upper를 기준으로 각 짝이 대비 되도록 수준을 변경한다.

df %>% mutate.(class = fct_relevel(
  class, "upper", after = 0L)) -> df1
levels(df1$class)

## [1] "upper"   "lower"   "working" "middle"

df1 %>% aov(hours ~ class, .) %>% summary()

##              Df Sum Sq Mean Sq F value Pr(>F)  
## class         3   1961   653.8   3.013 0.0297 *
## Residuals   496 107635   217.0                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

df1 %>% aov(hours ~ class, .) %>% summary.lm()

## 
## Call:
## aov(formula = hours ~ class, data = .)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -37.813  -4.813  -0.813   7.202  48.187 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    44.500      3.294  13.510   <2e-16 ***
## classlower    -11.750      4.658  -2.522    0.012 *  
## classworking   -2.205      3.423  -0.644    0.520    
## classmiddle    -3.687      3.448  -1.069    0.285    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 14.73 on 496 degrees of freedom
## Multiple R-squared:  0.0179, Adjusted R-squared:  0.01196 
## F-statistic: 3.013 on 3 and 496 DF,  p-value: 0.02975

8.2.3.2 대비계수

두 집단씩 짝을 구성해 비교한다. 즉, 두 집단으로 나누어 가며 비교한다.

이를 위해 먼저 대비계수를 구성한다.

0: 대비 대상에서 제외
음수: 기저 집단(비교 기준)
양수: 대비 집단
기저집단과 대비집단의 합 = 0

집단이 4개인 경우 다음과 같이 두 집단으로 나눠 가며 대비계수를 설정하는 방법은 2가지가 있다.

1, 2 vs 3, 4로 대비한 다음, 1 vs 2를 대비하고, 3 vs 4를 대비
1 vs 2 3 4로 대비한 다음, 2 vs 3 4를 대비하고, 3 vs 4를 대비

8.2.3.2.1 대비1

먼저 “1, 2 vs 3, 4로 대비한 다음, 1 vs 2를 대비하고, 3 vs 4를 대비”하는 방식으로 해보자.

data.table(
  구분 = c("lower", "working", "middle", "upper", "합"),
  대비1 = c(-1, -1, 1, 1, 0),
  대비2 = c(-1, 1, 0, 0, 0),
  대비3 = c(0, 0, -1, 1, 0)) %>% 
  pivot_longer.(-구분) %>% 
  pivot_wider.(names_from = 구분, values_from = value) %>% 
  select.(구분 = name, lower, working, middle, upper, 합) %>% 
  gt() %>% 
  tab_header("두 집단으로 나눠가며 대비계수 설정")

두 집단으로 나눠가며 대비계수 설정
구분	lower	working	middle	upper	합
대비1	-1	-1	1	1	0
대비2	-1	1	0	0	0
대비3	0	0	-1	1	0

대비계수를 분석할 변수에 투입한다.

contrast1 <- c(-1,-1,1,1)
contrast2 <- c(-1,1,0,0)
contrast3 <- c(0,0,-1,1)

contrasts(df$class) <- 
  cbind(contrast1, contrast2) %>% cbind(contrast3)

contrasts(df$class)

##         contrast1 contrast2 contrast3
## lower          -1        -1         0
## working        -1         1         0
## middle          1         0        -1
## upper           1         0         1

대비계수를 투입한 변수로 분산분석을 한다. 두 집단을 나누어 가며 차이를 비교한 결과가 산출된다.

df %>% aov(hours ~ class, .) %>% summary.lm()

## 
## Call:
## aov(formula = hours ~ class, data = .)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -37.813  -4.813  -0.813   7.202  48.187 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)      40.090      1.215  33.007   <2e-16 ***
## classcontrast1    2.567      1.215   2.114   0.0350 *  
## classcontrast2    4.772      1.711   2.789   0.0055 ** 
## classcontrast3    1.843      1.724   1.069   0.2855    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 14.73 on 496 degrees of freedom
## Multiple R-squared:  0.0179, Adjusted R-squared:  0.01196 
## F-statistic: 3.013 on 3 and 496 DF,  p-value: 0.02975

contrast1: lower + working class와 나머지 2개 집단 사이에 유의한 차이가 있다.
contrast2: lower class와 working class 사이에 유의한 차이가 있다.
contrast3: middle class와 upper class 사이에 유의한 차이가 없다.

8.2.3.2.2 대비2

이번에는 1 vs 2 3 4로 대비한 다음, 2 vs 3 4를 대비하고, 3 vs 4를 대비하는 방식으로 해보자.

data.table(
  구분 = c("lower", "working", "middle", "upper"),
  대비1 = c(-3, 1, 1, 1),
  대비2 = c(0, -2, 1, 1),
  대비3 = c(0, 0, -1, 1)) %>% 
  pivot_longer.(-구분) %>% 
  pivot_wider.(names_from = 구분, values_from = value) %>% 
  select.(구분 = name, lower, working, middle, upper) %>% 
  gt() %>% 
  tab_header("두 집단으로 나눠가며 대비계수 설정")

두 집단으로 나눠가며 대비계수 설정
구분	lower	working	middle	upper
대비1	-3	1	1	1
대비2	0	-2	1	1
대비3	0	0	-1	1

대비계수를 분석할 변수에 투입한다.

contrast1 <- c(-3,1,1,1)
contrast2 <- c(0,-2,1,1)
contrast3 <- c(0,0,-1,1)

contrasts(df$class) <- 
  cbind(contrast1, contrast2) %>% cbind(contrast3)

contrasts(df$class)

##         contrast1 contrast2 contrast3
## lower          -3         0         0
## working         1        -2         0
## middle          1         1        -1
## upper           1         1         1

대비계수를 투입한 변수로 분산분석을 한다. 두 집단을 나누어 가며 차이를 비교한 결과가 산출된다.

df %>% aov(hours ~ class, .) %>% tidy()

## # A tibble: 2 x 6
##   term         df   sumsq meansq statistic p.value
##   <chr>     <dbl>   <dbl>  <dbl>     <dbl>   <dbl>
## 1 class         3   1961.   654.      3.01  0.0297
## 2 Residuals   496 107635.   217.     NA    NA

df %>% aov(hours ~ class, .) %>% summary.lm()

## 
## Call:
## aov(formula = hours ~ class, data = .)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -37.813  -4.813  -0.813   7.202  48.187 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)     40.0896     1.2146  33.007  < 2e-16 ***
## classcontrast1   2.4465     0.8756   2.794  0.00541 ** 
## classcontrast2   0.1206     0.6529   0.185  0.85350    
## classcontrast3   1.8433     1.7240   1.069  0.28550    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 14.73 on 496 degrees of freedom
## Multiple R-squared:  0.0179, Adjusted R-squared:  0.01196 
## F-statistic: 3.013 on 3 and 496 DF,  p-value: 0.02975

contrast1: lower class와 나머지 3개 집단 사이에 유의한 차이가 있다.
contrast2: working class와 나머지 2개 집단 사이에 유의한 차이가 없다.
contrast3: middle class와 나머지 1개 집단 사이에 유의한 차이가 없다.

8.2.4 분석결과 보고

8.2.4.1 사후분석

분산분석에서 사후분석을 진행한 경우에는 1) 전체 모형에 대한 내용, 2) 사용한 사후분석 방법에 대한 내용 및 2) 유의한 사후분석 결과에 대한 내용이 포함돼야 한다.

분석결과 계층과 노동시간에 사이에는 통계적으로 유의한 관련성이 있었다, \(F\)(3, 496) = 3.01, \(p\) = 0.029. Tukey의 HSD를 이용하여 사후분석을 한 결과, 근로계층과 최하계층 사이에 통계적으로 유의한 차이가 있었다, \(p\) = 0.028. 최상계층과 최하계층 사이에는 유의수준 0.05에서 유의한 차이가 나타나지 않았다, \(p\) = 0.057.

8.2.4.2 가변수 계획비교

계획비교를 진행한 경우에는 사후분석과 달리, 사전가설에 대한 소개가 포함돼야 한다.

가변수를 설정해 최상계층과 다른 각 계층사이에 노동시간의 차이가 있는지 알아보기로 했다. 분석결과 계층과 노동시간에 사이에는 통계적으로 유의한 관련성이 있었다, \(F\)(3, 496) = 3.01, \(p\) = 0.029. 구체적으로는 최상계층의 노동시간은 최하계층의 노동시간보다 통계적으로 유의하게 짧았다, \(t\) = 2.52, p = 0.012. 그러나, 최상계층의 노동시간은 근로계층의 노동시간와 통계적으로 유의한 차이가 나타났지 않았, \(t\) = 0.64, \(p\) = 0.52, 중간계층과의 노동시간 사이에도 유의한 차이가 나타나지 않았다, \(t\) = 1.07, p = 0.29.

8.2.4.3 대비계수 계획비교

대비계수를 이용한 계획비교 결과는 다음과 같이 보고한다.

대비계수를 이용하며, 최하계층과 다른 상위 계층 사이에 노동시간에 차이가 있는지, 근로계층과 그의 상위 계층사이에 차이가 있고, 중간계층과 그의 상위계층 사이에 차이가 있는지 알아보기로 했다. 분석결과 계층과 노동시간에 사이에는 통계적으로 유의한 관련성이 있었다, \(F\)(3, 496) = 3.01, \(p\) = 0.029. 구체적으로 살펴보면, 최하계층의 노동시간은 다른 나머지 계층의 노동시간보다 통계적으로 유의하게 짧았다, \(t\) = 2.79, \(p\) = 0.005. 그러나, 근로계층과 다른 두 상위 계층과의 사이에는 통계적으로 유의한 차이가 없었다, \(t\) = 0.19, \(p\) = 0.853. 증간계층과 최상계층 사이에도 유의한 차이가 나타나지 않았다, \(t\) = 1.08, \(p\) = 0.285.

8.2.4.4 시각화

# 평균과 표준편차 표시하기 위해 데이터프레임에 값 포함
df %>% mutate.(
  m = mean(hours) %>% round(2), 
  sd = sd(hours) %>% round(2),
  .by = class) %>% 
# 도표  
ggplot(aes(x = class, y = hours, 
                 color = class)) +
  # ggforce패키지로 시나플롯 
  geom_sina(alpha = .3) +
  # 표준편차로 에러바 표시
  geom_errorbar(aes(x = class, y = m,
                    ymin = m - sd, ymax = m + sd),
                width = .2, color = 'dimgray') +
  # 평균 점으로 표시
  geom_point(aes(x = class, y = m), 
             color = 'dimgray', size = 3) +
  # 평균 텍스트로 표시
  geom_text(stat = 'summary',
            aes(label = paste("M:", round(..y.., 2))),
            color = 'black', size = 4, nudge_x = .33) +
  # ggpubr패키지로 p값 표시
  stat_compare_means(   # 전반적 모형의 p값
    method = 'anova', vjust = 1) +
  # Pairwise comparisons: Specify the comparisons
  # stat_compare_means(   
  #  comparisons = list(c("lower", "working"), # 비교대상
  #                     c("lower", "upper")),
  #  label.y = c(95, 110)) + # p값 위치(y축)
  stat_compare_means(
    method = 't.test', ref.group = "lower",
    label.y = c(110, 110, 110), hjust = 1) + 
  labs(title = "계층별 노동시간 차이",
       caption = "Note: M = 평균; 기준집단 = lower class",
       x = "계층",
       y = "주당 노동시간") + 
  theme(legend.position = 'none') +
  ylim(0, 140)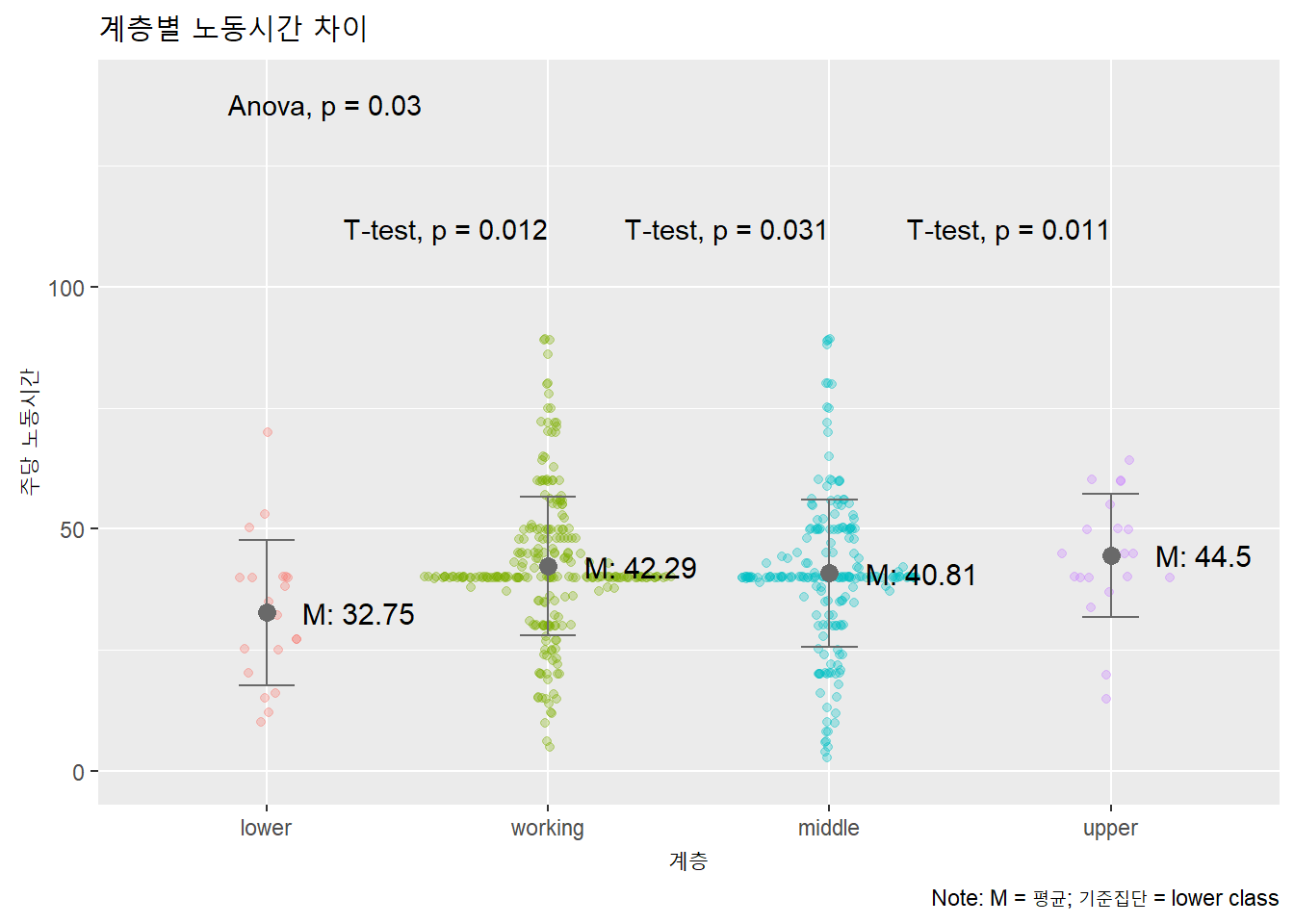

8.2.5 분산분석의 종류

분산분석은 투입하는 독립변수, 종속변수 및 통제변수의 갯수와 특성에 따라 다음과 같이 분류한다.

일원분산분석(One-way ANOVA):
- 단일 요인(독립변수)에 평균 비교. 요인의 수준(level)이 독립집단이므로 집단간 요인(between-subject factor).
반복측정분산분석(Repeated-measures ANOVA):
- 동일한 표본에 대해 2차례 이상 측정한 값 비교(e.g., 짝진 t검정). 요인의 수준이 동일집단이므로 집단내요인(within-subject factor).
다원분산분석(N-way ANOVA):
- N개의 집단간 요인(between-subject)의 상호작용 분석.
- 집단간 요인이 2개면 독립변수 2개 사이의 상호작용을 분석하므로 이원분산분석이라고 한다.
혼합분산분석(Mixed ANOVA):
- 집단간 요인(between-subject factor)과 집단내 요인(within-subject factor) 사이의 상호작용 분석.
공분산분석(Analysis of Covariance):
- 통제변수를 공변인(covariate)으로 투입한 일원분산분석.
다변량분산분석(Multivariate ANOVA):
- 연속형의 종속변수가 2개 이상인 분산분석

분산분석에 대해 추가적인 내용은 datanovia의 무료강좌 참조.

8.3 회귀분석

범주형 독립변수와 숫자형 종속변수의 관계는 가변수를 이용한 회귀분석을 통해서도 분석가능하다. 앞서 수행했던 GSS자료의 계층과 노동시간의 관계에 대한 일원분사분석을 회귀분석으로 다시 해보자.

gss %>% lm(hours ~ class, .) %>% summary()

## 
## Call:
## lm(formula = hours ~ class, data = .)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -37.813  -4.813  -0.813   7.202  48.187 
## 
## Coefficients:
##                    Estimate Std. Error t value Pr(>|t|)    
## (Intercept)          32.750      3.294   9.942   <2e-16 ***
## classworking class    9.545      3.423   2.789   0.0055 ** 
## classmiddle class     8.063      3.448   2.339   0.0198 *  
## classupper class     11.750      4.658   2.522   0.0120 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 14.73 on 496 degrees of freedom
## Multiple R-squared:  0.0179, Adjusted R-squared:  0.01196 
## F-statistic: 3.013 on 3 and 496 DF,  p-value: 0.02975

이 결과와 분산분석의 가변수 계획비교 결과와 비교해보자.

gss %>% aov(hours ~ class, .) %>% summary.lm()

## 
## Call:
## aov(formula = hours ~ class, data = .)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -37.813  -4.813  -0.813   7.202  48.187 
## 
## Coefficients:
##                    Estimate Std. Error t value Pr(>|t|)    
## (Intercept)          32.750      3.294   9.942   <2e-16 ***
## classworking class    9.545      3.423   2.789   0.0055 ** 
## classmiddle class     8.063      3.448   2.339   0.0198 *  
## classupper class     11.750      4.658   2.522   0.0120 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 14.73 on 496 degrees of freedom
## Multiple R-squared:  0.0179, Adjusted R-squared:  0.01196 
## F-statistic: 3.013 on 3 and 496 DF,  p-value: 0.02975

결과는 동일하다. 분산분석이 회귀분석의 특수한 사례이기 때문이다.

따라서 대비계수 조정을 통한 계획비교 결과와 회귀분석의 결과도 같다.

먼저 비교대상을 직교방식으로 비교 집단을 2개씩 나눠보자.

1 vs 2 3 4로 대비한 다음, 2 vs 3 4를 대비하고, 3 vs 4를 대비

contrast1 <- c(-3,1,1,1)
contrast2 <- c(0,-2,1,1)
contrast3 <- c(0,0,-1,1)

contrasts(df$class) <- 
  cbind(contrast1, contrast2) %>% cbind(contrast3)

contrasts(df$class)

##         contrast1 contrast2 contrast3
## lower          -3         0         0
## working         1        -2         0
## middle          1         1        -1
## upper           1         1         1

df %>% lm(hours ~ class, .) %>% summary()

## 
## Call:
## lm(formula = hours ~ class, data = .)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -37.813  -4.813  -0.813   7.202  48.187 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)     40.0896     1.2146  33.007  < 2e-16 ***
## classcontrast1   2.4465     0.8756   2.794  0.00541 ** 
## classcontrast2   0.1206     0.6529   0.185  0.85350    
## classcontrast3   1.8433     1.7240   1.069  0.28550    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 14.73 on 496 degrees of freedom
## Multiple R-squared:  0.0179, Adjusted R-squared:  0.01196 
## F-statistic: 3.013 on 3 and 496 DF,  p-value: 0.02975

contrast1: lower + working class와 나머지 2개 집단 사이에 유의한 차이가 있다.
contrast2: lower class와 working class 사이에 유의한 차이가 없다.
contrast3: middle class와 upper class 사이에 유의한 차이가 없다.

df %>% aov(hours ~ class, .) %>% summary.lm()

분산분석의 대비계수를 이용한 계획비교와 같은 결과다.

8.4 종합

8.4.1 통계

유의확률/유의도/\(p\)값
유의수준/\(\alpha\)
신뢰구간
이론기반 가설검정
시뮬레이션기반 가설검정
재표집(resampling)
부트스트래핑(bootstrapping)
퍼뮤테이션(순열: permutation)
t통계치
F통계치
분산분석(ANOVA)
일원분산분석(one-way ANOVA)
다원분산분석(n-way ANOVA)
반복측정분산분석(repeated-measure ANOVA)
혼합분산분석(mixed ANOVA)
공분산분석(ANCOVA)
다변량분산분석(multivariate MANOVA)
MSG
MSE
요인(factor)
수준(level)
사후분석(post-hoc analysis)
계획비교(planned comparison)
가변수(dummy variable)
대비계수
Tukey의 HSD
봉페르니 교정(Bonferroni correction)
FWER(FamilyWise Error Rate)

8.4.2 코딩

infer
- specify()
- hypothesize()
- generate()
- calculate()
- get_p_value()
- get_confidence_interval()
- visualize()
- shade_p_value()
- shade_ci()
ggplot2
- geom_errorbar()
- geom_point()
- geom_text()
ggpubr
- stat_compare_means()
ggforce
- geom_sina()
dplyr
- summarise()
- mutate()
- filter()
- select()
- group_by()
tidytable
- .by =
tidyr
- pivot_longer()
- pivot_wider()
stringr
- str_remove_all()
forcats
- fct_relevel()
TukeyHSD
summary.lm()
contrasts()
cbind()
aov()
t.test()
t_test()