9 가설검정2

c(
  "rio", "tidyverse", "tidytable", 
  "skimr", "janitor", "psych", "psychTools", "car",
  "tidymodels", "lm.beta", "mediation", "rstatix",
  "GGally", "ggforce", "mdthemes", "patchwork", "ggdag",
  "r2symbols", "equatiomatic", "gt", "ggpubr", "ggfortify" 
  ) -> pkg 
sapply(pkg, function(x){
  if(!require(x, ch = T)) install.packages(x, dependencies = T)
  library(x, ch = T)
})

9.1 가설검정과 인과추론

추론통계는 관측대상(표본)에 대한 정보를 연구대상(모집단)으로 일반화하는 방법이다.

모집단에 대한 전수조사를 하지 않고도 모집단의 특성을 추정할 수 있는 이유는 모집단의 분포에 대한 사전지식(정규분포, \(t\)분포, \(F\)분포 등)이 있기 때문이다.

관측한 현상의 통계치(평균의 차이, 기울기 등)가 영가설이 참일 경우의 모분포에서 발생확률이 낮다면, 관측값은 우연하게 나타난 것이 아니라고 판단할 수 있다.

우연이 아닐 가능성을 유의확률 \(p\)값으로 정량화하고 판단기준(유의수준)을 정해, 우연성 여부(통계적 유의성: statistical significance)를 판단한다.

관례적으로 0.05를 기준으로 통계적 유의성 여부를 판단하지만, 이는 어디까지나 관례적인 기준이므로 통계적 유의성을 과학적 유의성(scientific significance)으로 동일시해서는 안된다.

인과추론에 통계적 유의성을 활용하기 위해서는 적절한 연구설계가 필요하다. 연관성에 더하여 시간적 선후관계 및 제3변수의 영향을 고려해야 하기 때문이다.

이상적인 연구설계는 무작위통제시험(RCT: randominzed controlled trial)이다. 대조와 무작위 할당을 통해, 다른 모든 변수를 동일하게 통제하고 오직 원인에 대한 처치(treatment)만 비교할 수 있기 때문이다.

그러나 RCT가 현실적으로 가능하지 않은 경우가 적지 않다. 또한 통제된 환경에서의 실험이므로 외적타당도의 한계가 있다. 회귀단절설계(RDD: regression discontinuity design)는 RCT의 대안으로서 주목받는 인과추론 방법이다.

영국 국회의원의 의원직 획득과 의원 개인 자산의 증가에 대한 연구를 통해 가설검정의 원리를 복습하고, 회귀단절설계(RDD: regression discontinuity design)에 대해 학습한다(Imai 2018).

이를 위해 먼저 정규분포와 가설검정의 원리 및 표준화점수(z-score)로 유의확률 \(p\)값 계산하는 방법에 대해 학습한다.

9.1.1 정규분포

정규분포에 관련된 값을 생성하는 함수는 4종이 있다.

  • rnorm(n, mean = 0, sd = 1)
    • 정규분포를 이루는 임의 값 n개 생성.
  • dnorm(x, mean = 0, sd = 1, log = FALSE)
    • d(density): 밀도함수. x값에 대응하는 y값(확률밀도) 산출
  • pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
    • p(누적분포값): x값이 q일때, q까지의 면적에 해당하는 누적분포값 p 산출. dnorm()이 개별 y값을 산출한다면, pnorm()은 개별 y값들이 누적된 면적 산출.
  • qnorm(p, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
    • pnorm()의 역수 산출. 누적분포값 p를 투입하면, x값(p까지의 면적에 해당하는 x값) 산출

정규분포는 봉우리가 하나이고 좌우 대칭인 종모양의 곡선을 이루는 연속확률분포다. 정규분포는 평균(\(\mu\))과 분산(표준편차(\(\sigma\))의 제곱)을 지정해 생성하므로 표기법은 다음과 같다. \(N\)은 정규(normal).

\[ N(\mu, \sigma^2) \]

9.1.1.1 rnorm()

rnorm()은 정규분포를 이루는 값을 생성한다. 평균이 0이고, 표준편차가 1인 임의 값 900개를 점도표(dotplot)으로 geom_dotplot()함수로 표준정규분포도와 함께 표시해보자. 점도표의 점 하나가 개별 값을 의미한다.

data.frame(x = c(-4, 4), 
           rx = rnorm(n = 900), ry = 0.03) %>% 
  ggplot(aes(x = x)) +
  # 닷플롯 bin의 축을 x축으로 지정. 
  geom_dotplot(aes(rx, ry), binaxis = 'x', binwidth = 0.1, alpha = .5) +
  #geom_jitter(aes(rx, ry), alpha = .5, size = 3, height = .05) +
  stat_function(fun = dnorm, color = "DeepPink", size = 2) +
  labs(title = "rnorm(): 무작위로 생성된 개별 값", 
       x = "측정값(표준화)", y = "확률") +
  scale_x_continuous(breaks = seq(-4, 4, 1)) +
  theme_classic() +
  theme(title = element_text(size = 15)) + ylim(0, 0.4)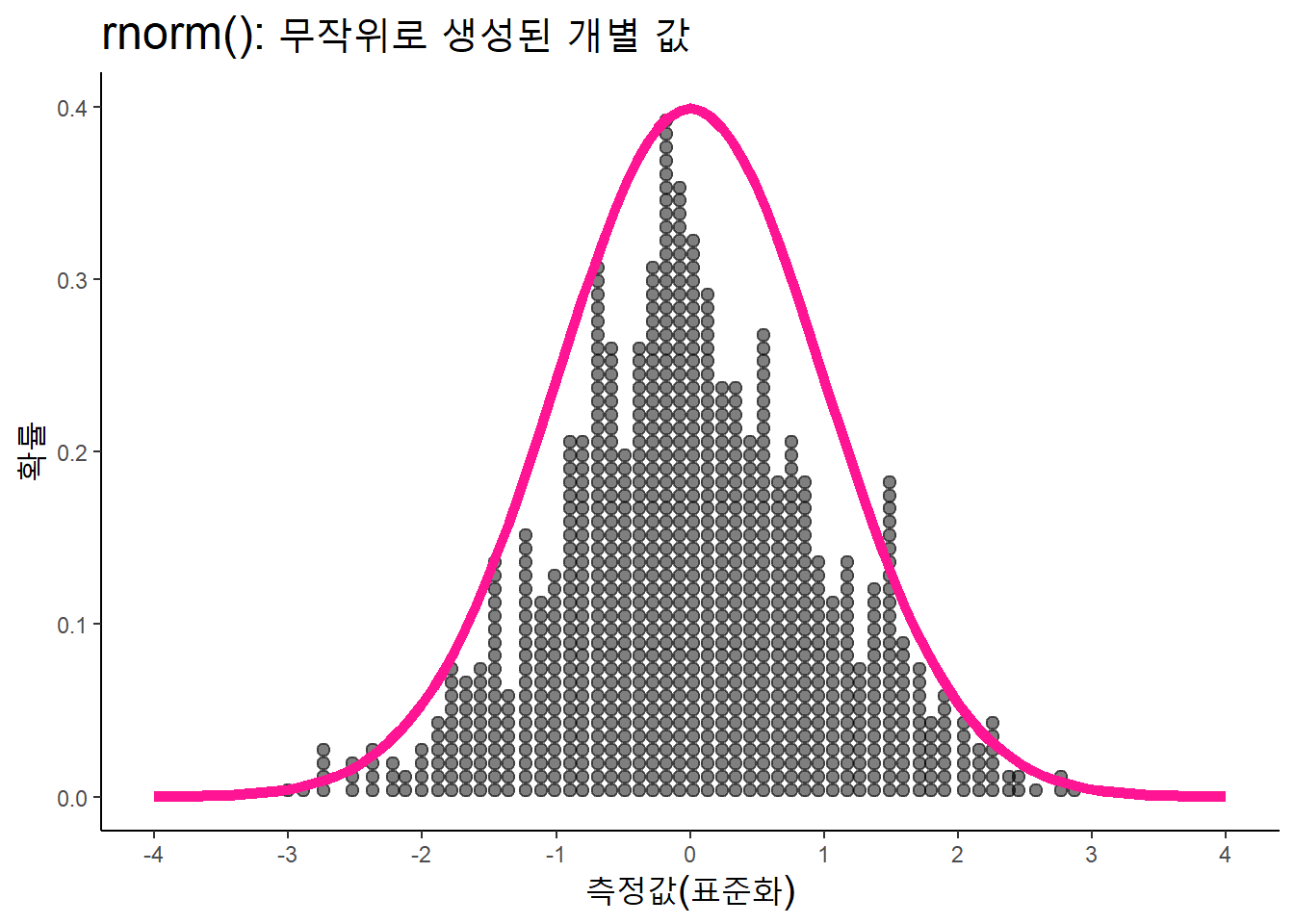

9.1.1.2 dnorm()

dnorm()은 확률밀도 함수. x축의 값에 대응하는 확률(y축의 값)을 산출한다. 즉, x축의 값을 투입하면, y축의 값을 산출한다. x축이 2인 경우, 확률밀도 y값은 0.054(5.4%의 확률).

dnorm(x = 2, mean = 0, sd = 1)
## [1] 0.05399097
data.frame(x = c(-4, 4)) %>% 
  ggplot(aes(x = x)) +
  stat_function(fun = dnorm, color = "DeepPink", size = 2) +
  # 주석
  annotate('text', x = 2, y = 0.1, 
           label = "dnorm(2) = 0.054", size = 5) +
  # 단방향 화살표
  annotate('segment', x = 2, xend = 2,
           y = -Inf, yend = dnorm(2),
           color = 'blue', size = 2,
           arrow = arrow(ends = 'last')) +
  # 가로선
  geom_hline(yintercept = dnorm(2),
             color = 'black', size = 2) +
  labs(title = "dnorm(): x축의 값에 대한 y축의 값(확률)", 
       x = "측정값(표준화)", y = "확률") +
  scale_x_continuous(breaks = seq(-4, 4, 1)) +
  theme_classic() +
  theme(title = element_text(size = 15))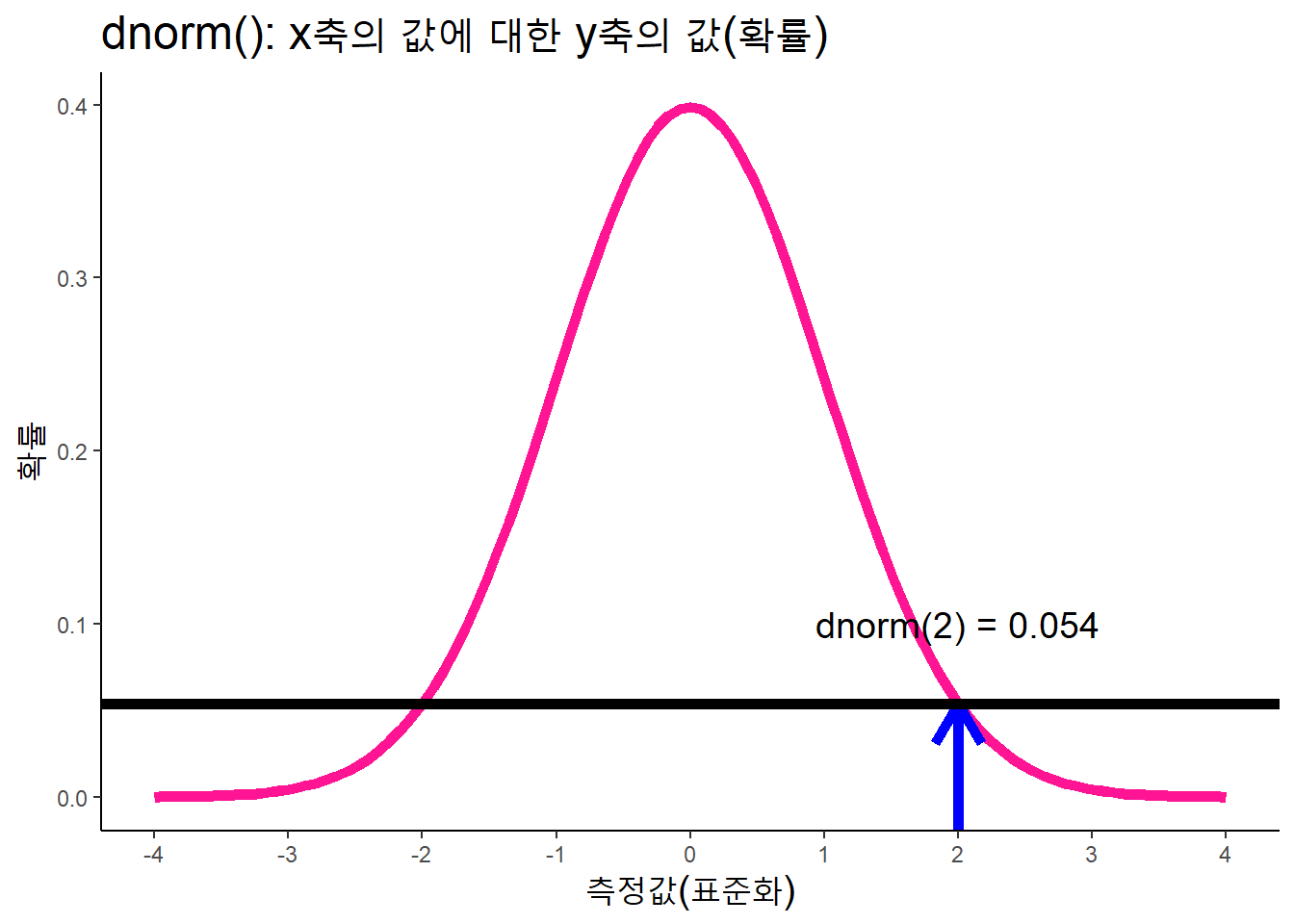

9.1.1.3 pnorm()

x축의 값이 q일때, q까지의 면적에 해당하는 확률 p를 산출한다.

  • 용법: pnorm(q, mean = 0, sd = 1, lower.tail = T, log.p = F)
    • q : x축의 값
    • mean : 평균
    • sd : 표준편차
    • lower.tail : 기본값은 작은 값 방향의 누적분포
    • log.p : 기본값은 FALSE. TRUE인 경우 log(p)

평균 50, 표준편차가 10인 정규분포에서 측정값 70보다 작은 값의 누적분포는 0.977

pnorm(70, mean = 50, sd = 10, lower.tail = T)
## [1] 0.9772499

기본값(mean = 0, sd = 1)은 표준화점수(Z: z-score) 이용

\[ Z = \frac{측정값 - mean}{SD} \]

측정값이 70, 평균 50, 표준편차가 10이면 표준화점수는 2.

obs_v <- 70
mean_v <- 50
sd_v <- 10
(obs_v - mean_v) / sd_v
## [1] 2
pnorm(q = 2, mean = 0, sd = 1, lower.tail = T)
## [1] 0.9772499

표준정규분포도에 2보다 작은 값의 누적분포를 표시하면 다음과 같다.

data.frame(x = c(-4, 4)) %>% 
  ggplot(aes(x = x)) +
  # 해당 영역 색으로 표시
  # 해당 영역 색으로 표시
  geom_area(stat = 'function', fun = dnorm, 
            fill = 'gray', xlim = c(-4, 2)) +
  #geom_rect(
  #  aes(xmin = -Inf, xmax = 2, ymin = -Inf, ymax = Inf),
  #  alpha = .2) +
  stat_function(fun = dnorm, color = "DeepPink", size = 2) +
  # 주석
  annotate('text', x = 0, y = dnorm(2)+.03, 
           label = "pnorm(2) = 0.977", size = 5) +
  # 양뱡향 화살표(ends = 'both')
  annotate('segment', x = 2, xend = -Inf, 
           y = dnorm(2), yend = dnorm(2),
           arrow = arrow(ends = 'both'), size = 2) +
  labs(title = "pnorm(): x축 값까지에 해당하는 확률 p(면적)", 
       x = "측정값(표준화)", y = "확률") +
  scale_x_continuous(breaks = seq(-4, 4, 1)) +
  theme_classic() +
  theme(title = element_text(size = 15))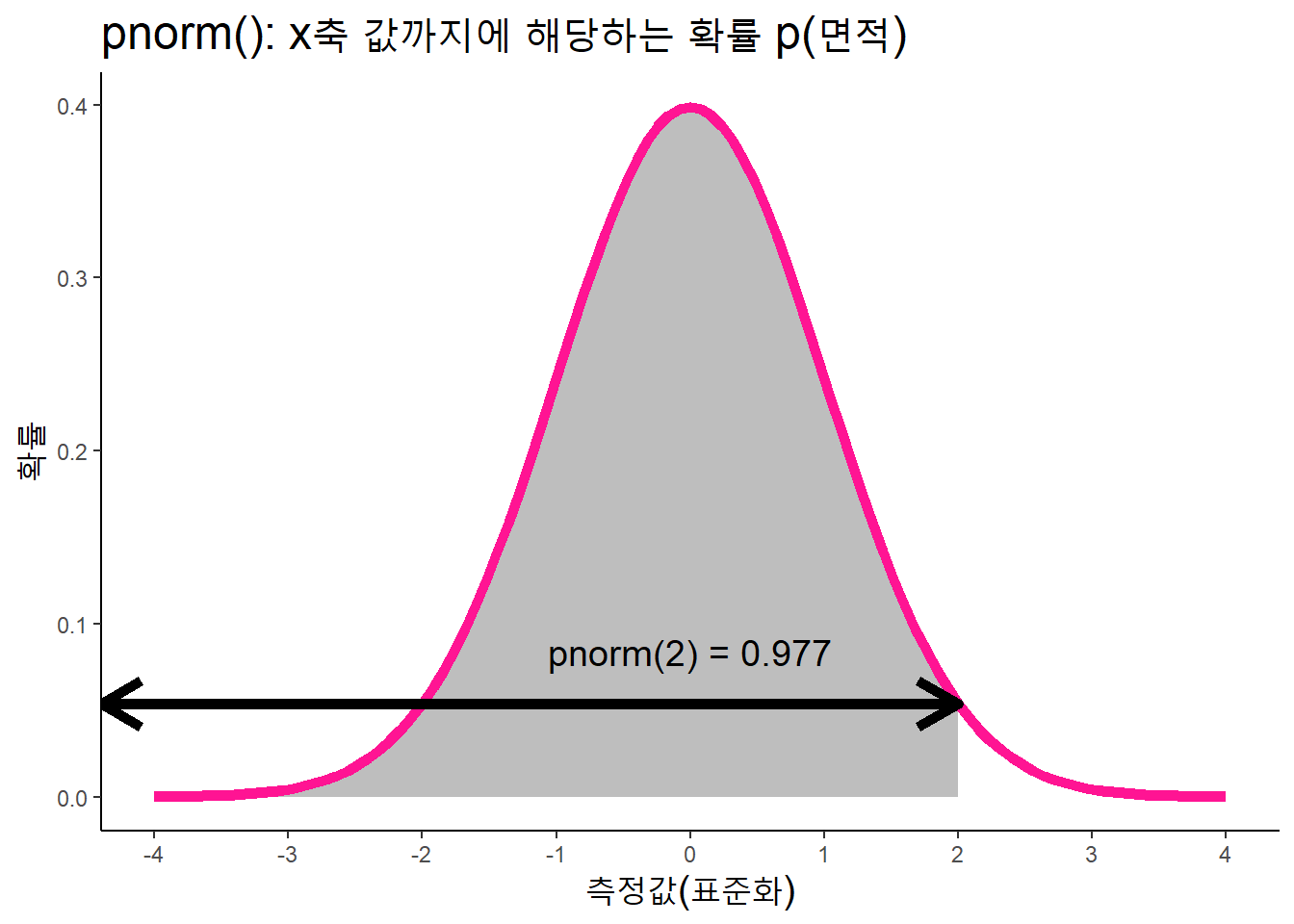

9.1.1.4 qnorm()

  • qnorm()은 pnorm()의 역수. 누적분포값 p를 투입하면, x축의 값(p까지의 면적에 해당하는값)을 산출한다.
qnorm(p = 0.9772499, mean = 0, sd = 1, lower.tail = T)
## [1] 2.000001
data.frame(x = c(-4, 4)) %>% 
  ggplot(aes(x = x)) +
  # 해당 영역 색으로 표시
  geom_area(stat = 'function', fun = dnorm, 
            fill = 'gray', xlim = c(-4, 2)) +
  stat_function(fun = dnorm, color = "DeepPink", size = 2) +
  # 주석
  annotate('text', x = 2, y = 0.1, 
           label = "qnorm(0.977) = 2", size = 5) +
  # 가로선
  annotate('segment', x = -Inf, xend = 2,
           y = dnorm(2), yend = dnorm(2),
           size = 2,
           arrow = arrow(ends = 'both')) +
  # 세로선
  annotate('segment', x = 2, xend = 2,
           y = -Inf, yend = dnorm(2),
           size = 2,
           arrow = arrow(ends = 'first')) +
  labs(title = "qnorm(): p까지의 면적에 해당하는 x축의 값", 
       x = "측정값(표준화)", y = "확률") +
  scale_x_continuous(breaks = seq(-4, 4, 1)) +
  theme_classic() +
  theme(title = element_text(size = 15))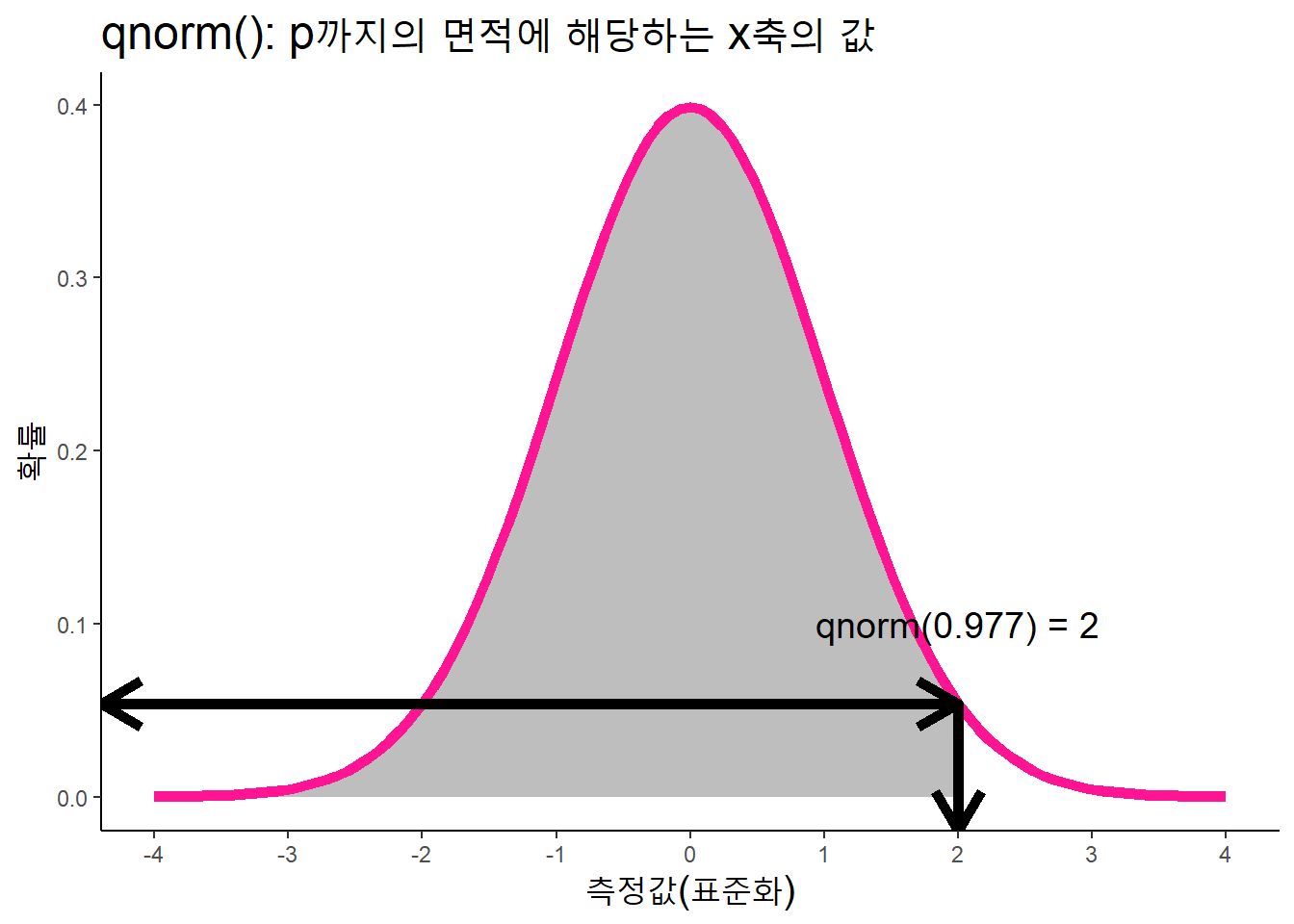

일반적으로 “자료가 정규분포를 따르는 분포인 경우, 약 68%가 1표준편차 안에, 95%가 2표준편차 안에, 그리고 99.7%는 3표준편차안에 있다. 평균이 0이고 표준편차가 1이면 \(평균-1\)과 \(평균+1\) 사이에 자료의 68%가 있고, \(평균-2\)과 \(평균+2\) 사이에 95%가 있고, \(평균-3\)과 \(평균+3\) 사이에 99.7%가 있다”고 하는데, pnorm()함수와 qnorm()함수를 확률분포의 면적이 95%가 되기 위한 정확한 x값을 계산해보자.

구간의 면적이 95%가 되기 위해서는 양쪽으로 2.5%씩 제해야 한다.

qnorm(0.025)
## [1] -1.959964
qnorm(0.975)
## [1] 1.959964
xmin_v <- qnorm(0.025)
xmax_v <- qnorm(0.975)

data.frame(x = c(-4, 4)) %>% 
  ggplot(aes(x = x)) +
  # 해당 영역 색으로 표시
  geom_area(stat = 'function', fun = dnorm, fill = 'gray', 
            xlim = c(-1.96, 1.96)) +
  stat_function(fun = dnorm, color = "DeepPink", size = 2) +
  # -1.96 주석
  annotate('text', x = -2, y = .4, 
           label = "qnorm(0.025) = -1.96", size = 5) +
  # -1.96 화살표
  annotate('segment', x = -1.96, xend = -1.96,
           y = -Inf, yend = 0.38,
           color = 'blue', size = 1.5, alpha = .3,
           arrow = arrow(ends = 'first')) +
  # 1.96 주석
  annotate('text', x = 2, y = .4, 
           label = "qnorm(0.975) = 1.96", size = 5) +
  # 1.96 화살표
  annotate('segment', x = 1.96, xend = 1.96,
           y = -Inf, yend = 0.38,
           color = 'blue', size = 1.5, alpha = .3,
           arrow = arrow(ends = 'first')) +
  # 97.5% 면적 주석
  annotate('text', x = -2.7, y = .3, 
           label = "pnorm(1.96) = 0.975", size = 5) +
  # 97.5% 면적 화살표
  annotate('segment', x = -Inf, xend = xmax_v, 
           y = .3 - .04, yend = .3 - .04,
           arrow = arrow(ends = 'first'), size = 1.2) +
  # 2.5% 면적 주석
  annotate('text', x = -2.7, y = .2-0.01, 
           label = "pnorm(-1.96) = 0.025", size = 5) +
  # 2.5% 면적 화살표
  annotate('segment', x = -Inf, xend = xmin_v, 
           y = .2 - .05, yend = .2 - .05,
           arrow = arrow(ends = 'first'), size = 1.2) +
  # 95% 면적 주석
  annotate('text', x = 0, y = .1, 
           label = "pnorm(1.96) - pnorm(-1.96) = 0.95", size = 5) +
  # 95% 면적 화살표
  annotate('segment', x = xmin_v, xend = xmax_v, 
           y = dnorm(2), yend = dnorm(2),
           arrow = arrow(ends = 'both'), size = 2) +
  
  labs(title = "95%확률의 면적", 
       x = "측정값(표준화)", y = "확률") +
  scale_x_continuous(breaks = seq(-4, 4, 1)) +
  theme_classic() +
  theme(title = element_text(size = 15))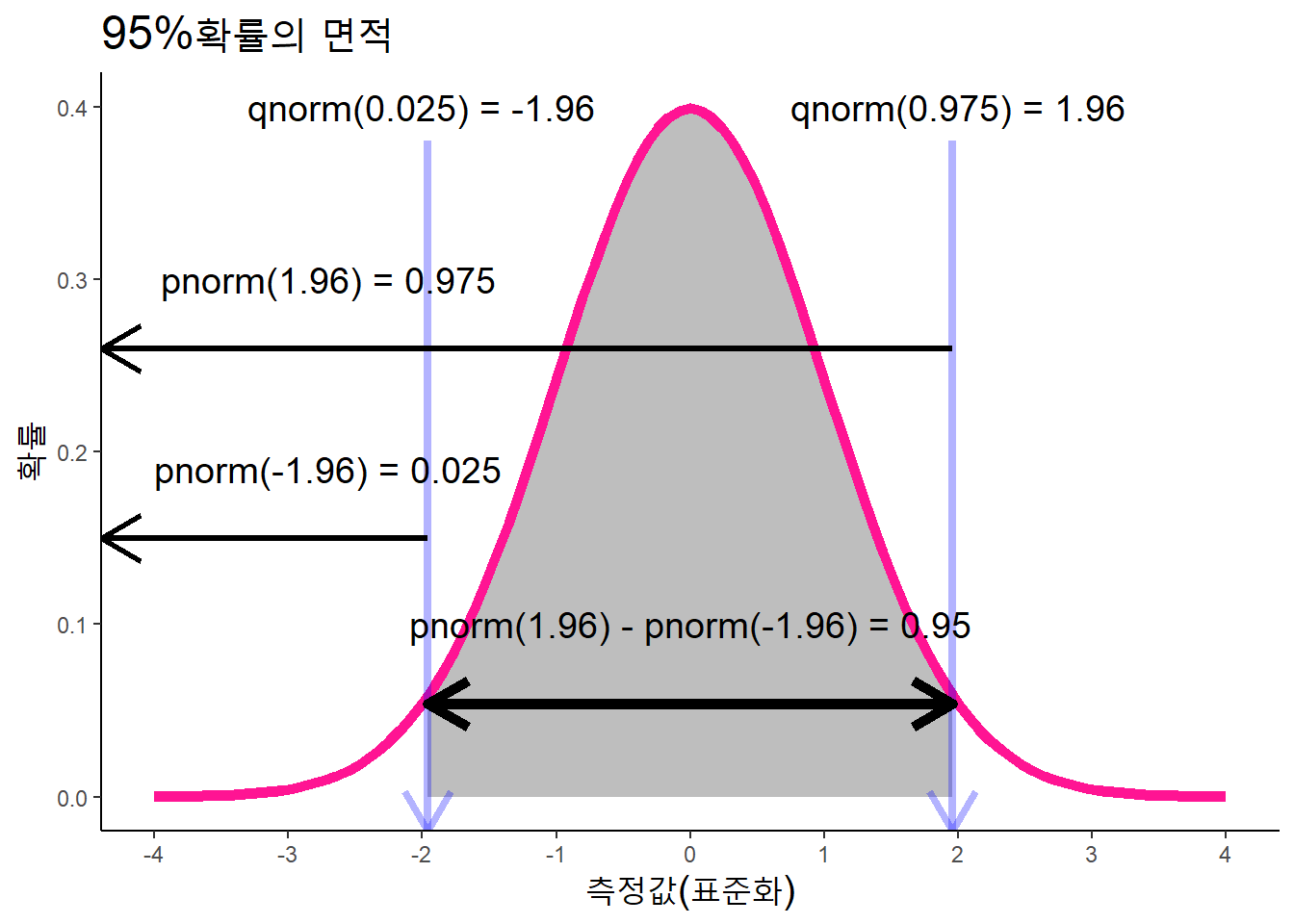

9.2 선형회귀모형

9.2.1 연구가설

미국 하버드대와 MIT연구자들은 정당에 따라 국회의원직 획득이 개인 자산 증가에 차별적으로 미치는 영향에 주목했다. 국회의원은 정치적 영향력을 행사할 수 있어 기업으로부터 직간접적인 이익을 취할 수 있지만, 노조에 정치적 기반을 둔 정당(예: 영국노동당)은 기업으로부터의 이익을 취하기 어렵다. 반면, 노조에 정치적 기반을 두지 않은 정당(예: 영국토리당) 의원은 기업으로부터 취하는 이익이 많다. 이 현상을 확인하기 위해 연구진은 연구시점 최근 사망한 의원의 득표율과 사망전후의 재산 자료를 분석했다 (Eggers and Hainmueller 2009).

  • 연구가설: 토리당 후보는, 노동당 후보와 달리, 당선 이후 재산이 증가할 것이다.
  • \(H_0\): 토리당 후보의 당선이전 자산 = 당선이후 자산

9.2.2 자료 가져오기

1950년부터 1970년 사이 총선에 출마한 후보자 사망 당시 개인자산 정보 수집.

"https://raw.githubusercontent.com/dataminds/art/main/files/MPs.csv" %>%
  rio::import() -> df
summary(df)
##    surname           firstname            party              ln.gross     
##  Length:427         Length:427         Length:427         Min.   : 8.433  
##  Class :character   Class :character   Class :character   1st Qu.:12.135  
##  Mode  :character   Mode  :character   Mode  :character   Median :12.461  
##                                                           Mean   :12.619  
##                                                           3rd Qu.:13.098  
##                                                           Max.   :16.311  
##                                                                           
##      ln.net            yob            yod         margin.pre      
##  Min.   : 6.981   Min.   :1890   Min.   :1984   Min.   :-0.54897  
##  1st Qu.:11.907   1st Qu.:1912   1st Qu.:1990   1st Qu.:-0.16293  
##  Median :12.403   Median :1919   Median :1996   Median :-0.07927  
##  Mean   :12.439   Mean   :1919   Mean   :1995   Mean   :-0.07361  
##  3rd Qu.:13.079   3rd Qu.:1926   3rd Qu.:2001   3rd Qu.:-0.01589  
##  Max.   :16.304   Max.   :1945   Max.   :2005   Max.   : 0.71210  
##                   NA's   :2                     NA's   :83        
##     region              margin        
##  Length:427         Min.   :-0.48631  
##  Class :character   1st Qu.:-0.12919  
##  Mode  :character   Median :-0.05096  
##                     Mean   :-0.04646  
##                     3rd Qu.: 0.03010  
##                     Max.   : 0.36797  
## 
glimpse(df)
## Rows: 427
## Columns: 10
## $ surname    <chr> "Llewellyn", "Morris", "Walker", "Walker", "Waring", "Brown~
## $ firstname  <chr> "David", "Claud", "George", "Harold", "John", "Ronald", "Le~
## $ party      <chr> "tory", "labour", "tory", "labour", "tory", "labour", "tory~
## $ ln.gross   <dbl> 12.13591, 12.44809, 12.42845, 11.91845, 13.52022, 12.46052,~
## $ ln.net     <dbl> 12.135906, 12.448091, 10.349009, 12.395034, 13.520219, 9.63~
## $ yob        <int> 1916, 1920, 1914, 1927, 1923, 1921, 1907, 1912, 1905, 1920,~
## $ yod        <int> 1992, 2000, 1999, 2003, 1989, 2002, 1987, 1984, 1998, 2004,~
## $ margin.pre <dbl> NA, NA, -0.057168204, -0.072508894, -0.269689620, 0.3409586~
## $ region     <chr> "Wales", "South West England", "North East England", "Yorks~
## $ margin     <dbl> 0.05690404, -0.04973833, -0.04158868, 0.02329524, -0.230005~
  • surname: 후보자 성
  • firstname: 후보자 이름
  • party: 후보자 소속 정당(labour or tory)
  • ln.gross: 사망시점 총자산의 로그
  • ln.net: 사망시점 순자산의 로그
  • yob: 후보자 출생연도
  • yod: 후보자 사망연도
  • margin.pre: 이전 선거에서 후보자 소속 정당의 승리마진
  • region: 선거구
  • margin: 승리마진(득표율)

9.2.2.1 로그변환

소득이나 인구와 같은 변수에는 극단적으로 큰 값 혹은 작은 값들이 포함돼 값의 분포가 과도하게 편향된 분포를 이루는 경우가 있다. 영국 국회의원 소득자료도 큰 값이 매우 적고, 작은 값들이 과도하게 많다.

위 자료에서 ln.gross와 ln.net은 로그를 취한 값이다. 로그를 취하기 전 값의 분포를 나타내면 다음과 같다.

  • 지수함수 exp()는 로그를 취한 값의 역수를 산출한다.
df$ln.net %>% exp() -> net
ggplot() + aes(net) + geom_histogram(color = 'purple') +
  labs(title = "로그를 취하지 않은 손자산의 분포: 히스토그램")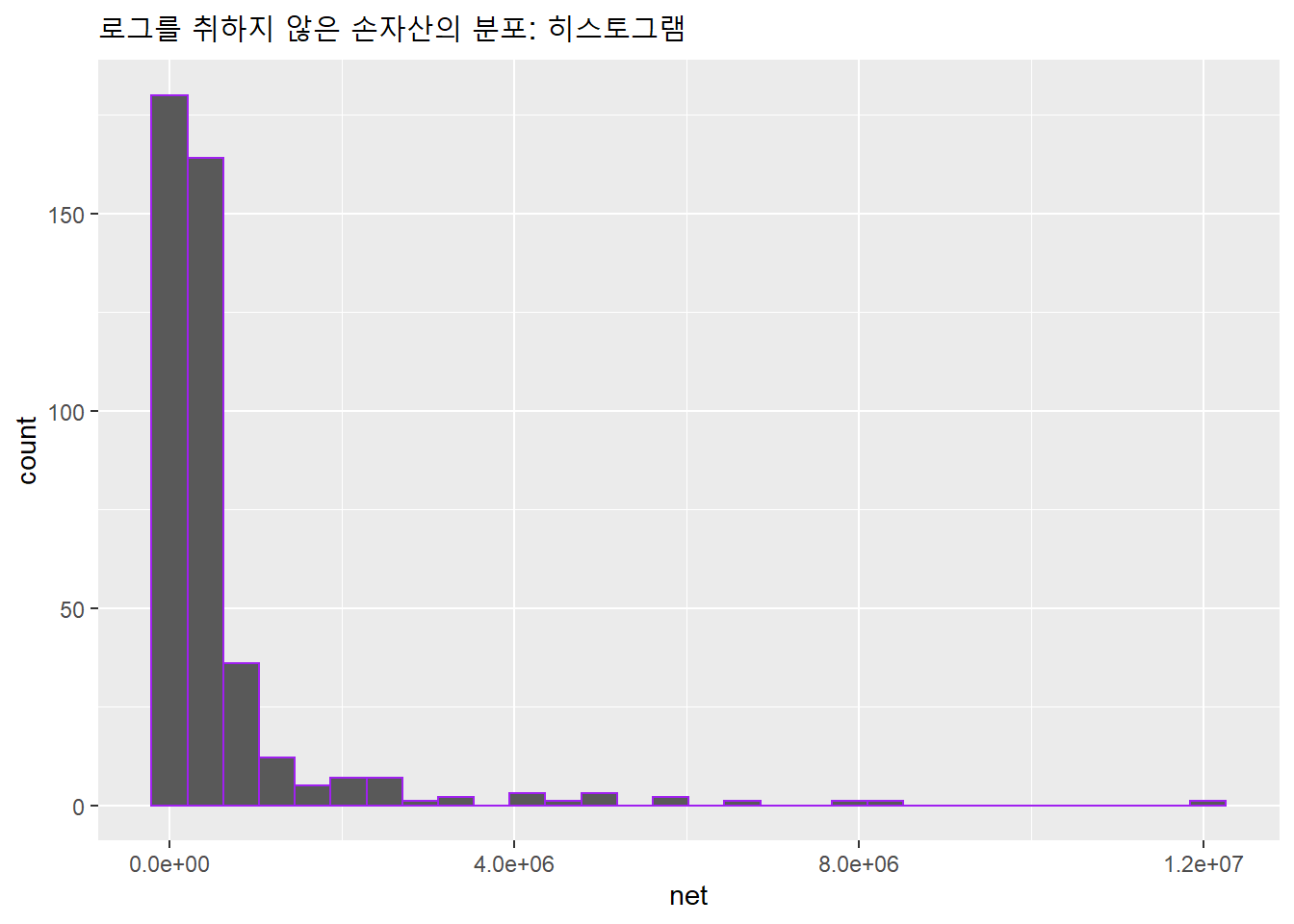

로그변환을 하면 변수의 비대칭성을 보정해 편향된 분포를 치우지지 않도록 할수 있다.

ggplot() + aes(log(net)) + 
  geom_histogram(color = 'pink') +
  labs(title = "로그변환을 한 순자산의 분포: 히스토그램")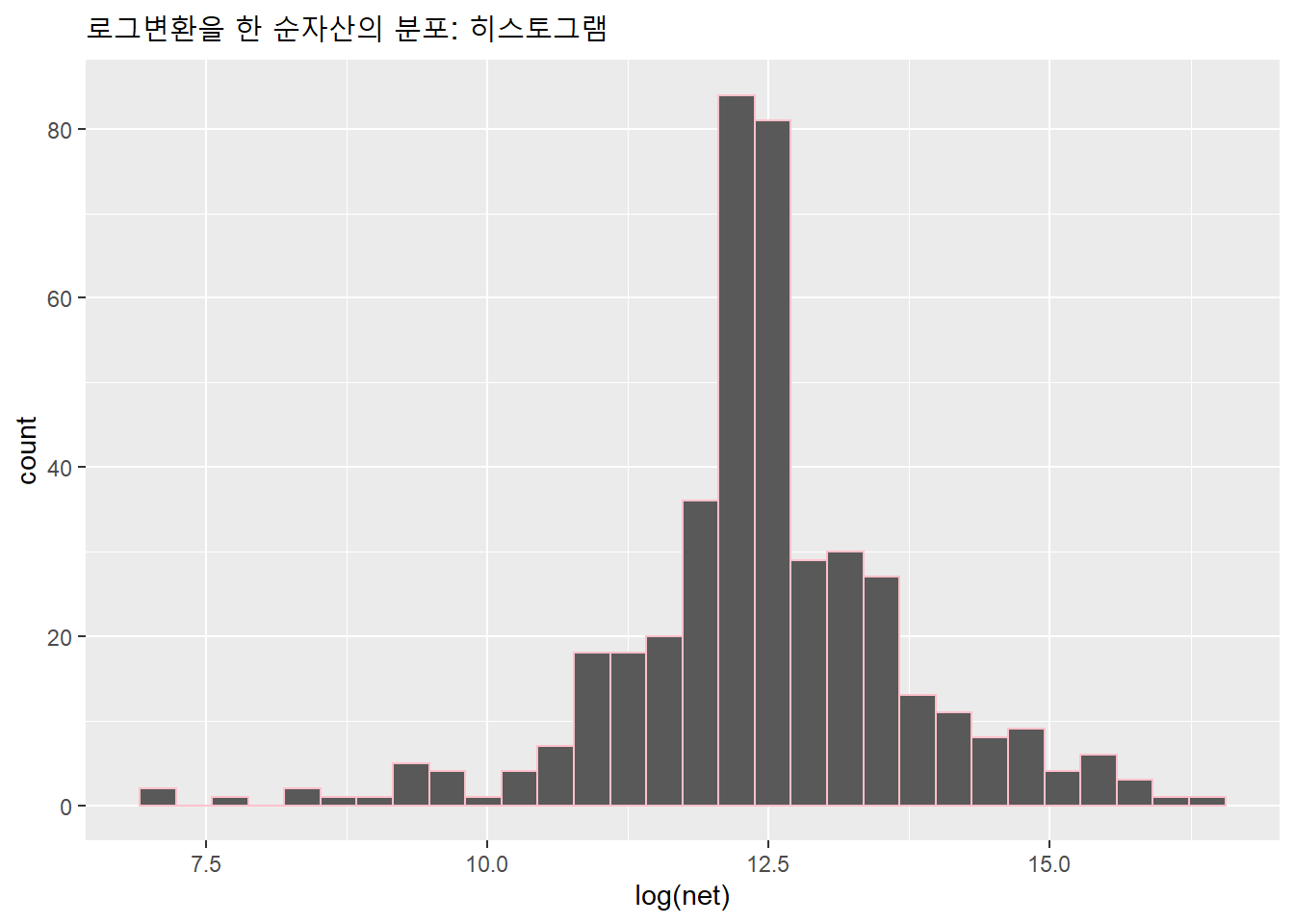

9.2.2.2 로그와 지수

큰수의 곱하기와 나누기를 간편하게 할수 있도록 고안된 개념.

밑(base)이 \(b\)인 양수 \(x\)의 로그와 지수(exponent) y의 관계는 다음과 같이 나타낼 수 있다.

왼쪽이 로그함수, 오른쪽이 지수함수

\[ y = log_b x ⇔ x = b^y \]

\[ 3 = log_{2}8 ⇔ 8 = 2^3 \]

  • 멱(power): 거듭제곱
  • 지수(exponent): 거듭제곱된 횟수. 즉, 밑을 곱한 횟수.
  • 밑(base): 거듭제곱할 값. 기수라고도 한다.
  • 로그(log): 지수의 역수. 고정된 밑을 몇번 곱해야 하는지 나타낸다.

9.2.2.3 로그와 지수함수 용법

  • log(x, base)

8에 밑이 2인 로그를 취하면 3이 된다.

log(x = 8, base = 2) == 3
## [1] TRUE

즉, 2를 3번 곱하면 8이 된다.

2^3 == 8
## [1] TRUE

log()함수에서 base(밑)의 기본값은 e( = 2.7182…)로서 자연로그한 값을 산출한다.

log(8)
## [1] 2.079442

로그함수log()는 지수exp()함수의 역함수

exp(log(8))
## [1] 8

R에는 밑이 10인 로그함수는 log10(), 밑이 2인 로그함수는 log2()로 별도의 함수가 제공된다.

log10(1000) == log(1000, base = 10)
## [1] TRUE
log2(8) == log(8, base = 2)
## [1] TRUE

밑이 자연수 10인 로그를 상용로그(common log)라고 한다.

9.2.3 기술통계

먼저 기술통계부터 구한다.

skimr::skim(df)
Table 9.1: Data summary
Name df
Number of rows 427
Number of columns 10
_______________________
Column type frequency:
character 4
numeric 6
________________________
Group variables None

Variable type: character

skim_variable n_missing complete_rate min max empty n_unique whitespace
surname 0 1 3 15 0 379 0
firstname 0 1 3 13 0 161 0
party 0 1 4 6 0 2 0
region 0 1 0 24 1 12 0

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
ln.gross 0 1.00 12.62 1.07 8.43 12.14 12.46 13.10 16.31 ▁▁▇▂▁
ln.net 0 1.00 12.44 1.27 6.98 11.91 12.40 13.08 16.30 ▁▁▇▅▁
yob 2 1.00 1918.59 9.68 1890.00 1912.00 1919.00 1926.00 1945.00 ▁▅▇▅▁
yod 0 1.00 1995.35 6.40 1984.00 1990.00 1996.00 2001.00 2005.00 ▆▅▅▇▇
margin.pre 83 0.81 -0.07 0.14 -0.55 -0.16 -0.08 -0.02 0.71 ▁▇▅▁▁
margin 0 1.00 -0.05 0.12 -0.49 -0.13 -0.05 0.03 0.37 ▁▃▇▃▁

관심변수의 관계를 살펴보자.

df %>% select.(ln.net, margin, party) %>% 
  ggpairs(aes(color = party))
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.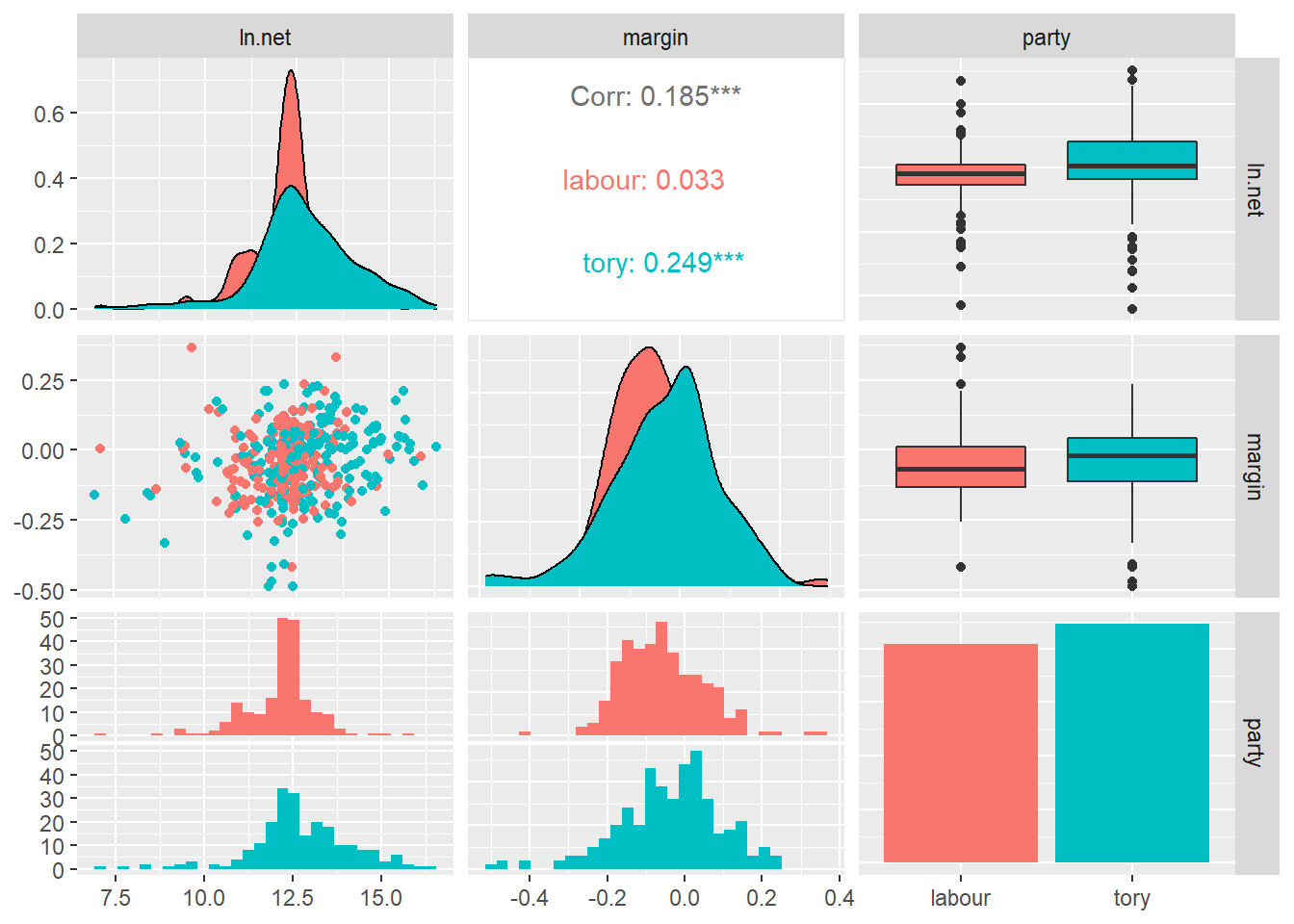

9.2.4 예비분석

득표율과 정당을 상호작용항으로 투입해 순자산에 대해 회귀분석을 하면, 정당별로 득표율과 순자산의 관계가 달리 나타남을 알 수 있다.

df %>% 
  ggplot(aes(margin, ln.net, color = party)) +
  geom_point() +
  geom_smooth(method = 'lm') +
  labs(title = "정당별 국회의원 득표율과 순자산 관계",
       x = "득표율",
       y = "순자산(로그)",
       color = "정당")
## `geom_smooth()` using formula 'y ~ x'

정당과 득표율 사이의 상호작용 여부를 확인하기 위해 회귀모형을 3개 만들어 분석 하면 다음과 같다.

먼저 회귀모형 3개를 만든다.

df %>% select.(ln.net, margin, party) -> df3
#names(df) <- c("순자산", "득표율", "정당")
y <- 1
x1 <- 2        # 순자산 ~ 득표율  
x2 <- 3
xx <- c(x1,x2) # 순자산 ~ 득표율 + 정당
               # 순자산 ~ 득표율 * 정당
### 회귀분석결과 표 생성 사용자함수
moderation_f <- function(df, y, x1, xx) {
## 변수 및 회귀모형
  # 변수
  dv <- names(df)[y]
  iv1 <- names(df)[x1]
  iv2 <- names(df)[xx]
  # 모형1 회귀식
  fml_mdl1 <- iv1 %>%
    paste0(., collapse = " + ") %>%
    paste0(dv, " ~ ", .)
  # 모형2 회귀식
  fml_mdl2 <- iv2 %>%
    paste0(., collapse = " + ") %>%
    paste0(dv, " ~ ", .)
  # 모형3 회귀식
  fml_mdl3 <- iv2 %>%
    paste0(., collapse = " * ") %>%
    paste0(dv, " ~ ", .)
## 회귀분석 + 데이터프레임결합
  model <- c(fml_mdl1, fml_mdl2, fml_mdl3)
  return(model)
} 
moderation_f(df3, y, x1, xx) -> model
data.frame(Formulas = model) %>% gt()
Formulas
ln.net ~ margin
ln.net ~ margin + party
ln.net ~ margin * party

각 회귀모형에 대해 회귀분석 3회 실시.

nn <- length(xx) + 1 + 1 # IV행 + 절편행 + 상호작용행 갯수
### 회귀분석 사용자함수
reg_f <- function(nn, model){  
  output <- list()
  for (i in seq_along(model)) {
    fit <- df %>% lm(model[i], .)
    # 변수명, 회귀계수, 표준오차 데이터프레임
    op <- tidy(fit)[1:nn, -4] %>% # statitic열 빼고 선택
      # 결정계수 데이터프레임
      bind_rows.(data.frame(
        term = c("결정계수",
                 "수정결정계수"),
        estimate = NA,
        std.error = c(summary(fit)$r.squared,
                     summary(fit)$adj.r.squared),
        p.value = NA
      ))
    output <- list(output, op)
  }
  return(output)
}
reg_f(nn, model) -> fit

3회 실시한 회귀분석 결과 표에 정리

## 모형3개 결합해 표로 정리
tbl_three <- function(df, fit){
  fit[[1]][[1]][[2]] %>%
    bind_cols.(fit[[1]][[2]]) %>%
    bind_cols.(fit[[2]]) %>%
    select.(term = term...9, # 모형3 변수명
            estimate...2:p.value...4, 
            estimate...6:p.value...8,
            estimate...10:p.value...12
            ) %>%
    gt() %>%
    tab_header(str_glue("{names(df)[y]}에 대한 회귀분석결과")) %>%
    fmt_number(-1, decimals = 2) %>%
    fmt_number(starts_with("p.value"), decimals = 3) %>%
    fmt_missing(-1, missing_text = html("<br>")) %>%
    cols_label(
      term = md("IV"),
      estimate...2 = md("_B_"),
      std.error...3 = md("_SE_"),
      p.value...4 = md("_p_"),
      estimate...6 = md("_B_"),
      std.error...7 = md("_SE_"),
      p.value...8 = md("_p_"),
      estimate...10 = md("_B_"),
      std.error...11 = md("_SE_"),
      p.value...12 = md("_p_")
    ) %>%
    tab_spanner(
      label = str_glue("Model 1"),
      columns = estimate...2:p.value...4) %>%
    tab_spanner(
      label = str_glue("Model 2"),
      columns = estimate...6:p.value...8) %>%
    tab_spanner(
      label = str_glue("Model 3"),
      columns = estimate...10:p.value...12) %>%
    text_transform(
      locations = 
        cells_body(
          columns = term,
          rows = term == "결정계수"),
      fn = function(x) {html(
          "<p align='center'><em>R<sup>2</sup></em></p>")
        }) %>% 
    text_transform(
      locations = 
        cells_body(
          columns = term,
          rows = term == "수정결정계수"),
      fn = function(x) {html(
          "<p align='center'><em>R<sup>2</sup><sub>adj</sub></em></p>")
        }) %>% 
    tab_footnote(
      footnote = str_glue("N = {nrow(df)}"),
      locations = cells_title()
    )
}
tbl_three(df3, fit)
ln.net에 대한 회귀분석결과1
IV Model 1 Model 2 Model 3
B SE p B SE p B SE p
(Intercept) 12.53 0.06 0.000 12.25 0.09 0.000 12.17 0.10 0.000
margin 1.91 0.49 0.000 1.76 0.48 0.000 0.31 0.78 0.696
partytory


0.53 0.12 0.000 0.64 0.13 0.000
margin:partytory





2.34 0.99 0.019

R2
0.03

0.08

0.09

R2adj
0.03

0.07

0.08
1 N = 427

득표율과 순자산 증가 사이에 통계적으로 유의한 연관이 있다, \(\beta\) = 1.91, \(p\) < 0.001. 정당도 순자산 사이에 통계적으로 유의한 연관이 있어, 노동당에 대하여 토리당인 경우 .53단위의 자산이 증가한다 \(\beta\) = 0.53, \(p\) < 0.001. 득표율과 정당의 상호작용도 통계적으로 유의하다, \(p\) = 0.019.

이를 통해 영가설(토리당 후보의 당선이전 자산 = 당선이후 자산)을 기각하고 대립가설을 채택한다. 이는 토리당 후보는, 노동당 후보와 달리, 당선 이후 재산이 증가할 것이라는 연구가설에 대한 근거가 된다.

그러나, 선형회귀모형으로는 투입한 변수 이외의 다른 여러 변수의 작용 가능성을 배제하기 어렵다. 국회의원 된 사람과 안 된 두 집단의 특성에 다양한 변수가 작용하기 때문이다. 따라서 가능한 다른 모든 변수의 영향을 배제하기 위해서는 가까스로 당선한 후보와 아깝게 탈락한 후보의 자산 증가를 비교할 필요가 있다.

만일 의원직이 자산 증가에 기여한다면, 특정 후보의 득표율이 음수에서 양수로 바뀐 지점의 의원(즉, 가까스로 당선한 의원)의 자산이 양의 방향으로 크게 증가하는 것을 기대할 수 있다. 자산 증가의 단절(discontinuity) 지점이 발생할 수 있다.

9.3 회귀단절설계

회귀단절설계(RDD: regression discontinuity design)는 무작위통제시험(RCT)을 하기 어려운 상황에서 인과추론을 위해 고안됐다. 소개된지는 꽤 오래됐지만, 2000년대 이후 활용이 급증하고 있는 분석방법이다.

회귀단절설계는 ’단절’이란 명칭에서 드러나듯, 처치로 작용할만한 요소를 기준으로 회귀선을 단절하여 비교하는 방법이다. 아래 도표는 영국 국회의원 선거에서 득표율과 의원 후보의 순자산(로그)의 관계를 나타냈다. 득표율이 양수면 의원 당선이고, 음수면 낙선이다.

득표율 당락지점(0)을 기준으로 당선된 후보(양의 득표율)와 탈락한 후보(음의 득표율)를 정당(party: labour vs. tory)별로 구분해 산점도와 회귀선으로 시각화하면 다음과 같은 결과를 얻을 수 있다.

df %>% 
  mutate.(margin0 = ifelse(margin < 0, margin, 0), # 낙선자 부분선택
          margin1 = ifelse(margin > 0, margin, 0), # 당선자 부분선택
          D = ifelse(margin > 0, 1, 0)) %>%  # 당락 분리
  filter.(party == "labour") %>%   # 소속정당 부분선택
ggplot(aes(margin, ln.net, color = factor(D))) + # 당락분리 변수가 요인
  geom_point(alpha = .3) +
  geom_smooth(  # 낙선자 회귀선
    aes(margin0, ln.net), method = 'lm', se = F, size = 3) +
  geom_smooth(  # 당선자 회귀선
    aes(margin1, ln.net), method = 'lm', se = F, size = 3) +
  labs(title = "노동당의 득표율과 순자산 관계: 단절구분",
       x = "득표율(margin)",
       y = "순자산(로그: ln.net)",
       color = "당락(D)")
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'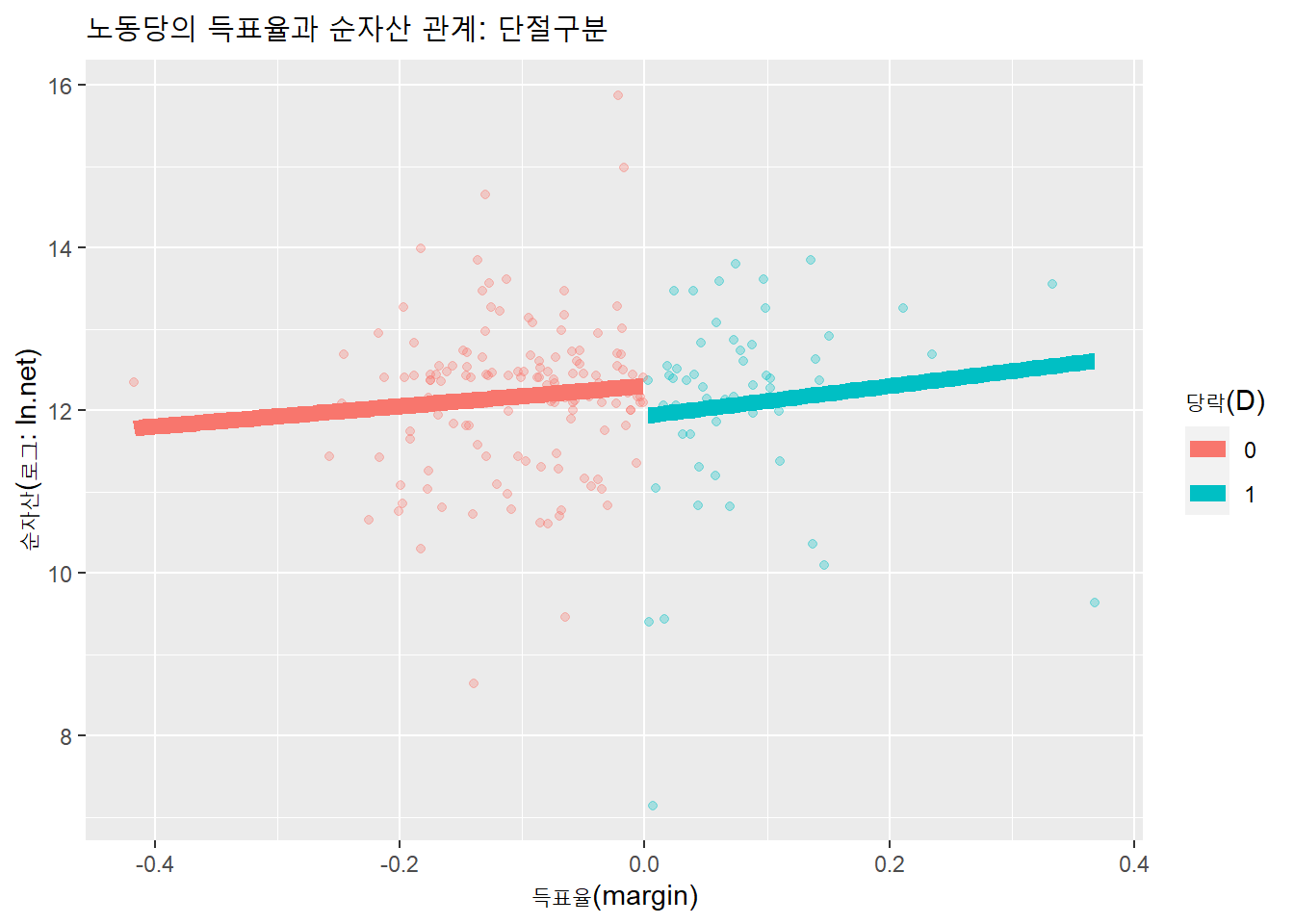

df %>% 
  mutate.(margin0 = ifelse(margin < 0, margin, 0),
          margin1 = ifelse(margin > 0, margin, 0),
          D = ifelse(margin > 0, 1, 0)) %>% 
  filter.(party == "tory") %>% 
ggplot(aes(margin, ln.net, color = factor(D))) +
  geom_point(alpha = .3) +
  geom_smooth(
    aes(margin0, ln.net), method = 'lm', se = F, size = 3) +
  geom_smooth(
    aes(margin1, ln.net), method = 'lm', se = F, size = 3) +
  labs(title = "토리당의 득표율과 순자산 관계: 단절구분",
       x = "득표율(margin)",
       y = "순자산(로그: ln.net)",
       color = "당락(D)")
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'

두 정당 모두 득표율을 기준으로 단절이 발생한다. 이 표본을 통해 관측된 단절이 통계적으로 유의한 차이가 있는지 검정해보자.

이를 위해 먼저 predict() 함수의 용법부터 학습하자.

9.3.1 predict()

predict()함수는 lm() 이나 glm() 등으로 산출한 모형을 이용해 새로운 자료에 대한 예측값을 산출한다.

인자로 주어진 모형(lm, glm 등)에 따라 내부적으로 predict.lm( ), predict.glm( ) 등의 함수로 처리한다.

lm()을 이용해 산출한 선형회귀모형인 경우 predict.lm( )로 처리한다.

  • predict.lm(object, newdata, se.fit = FALSE, interval = c("none", "confidence", "prediction"), level = 0.95, ...)
    • object: lm()으로 산출한 선형모형
    • newdata: 예측에 사용할 새로운 데이터(데이터프레임). newdata를 투입하지 않으면, 기존 투입한 모형계산에 사용한 자료로 계산.
    • se.fit: 표준오차. 기본값은 FALSE
    • interval: 구간의 종류. 기본값은 ‘none.’ 신뢰구간을 계산하려면 ‘interval’ 투입. 회귀계수의 신뢰구간으로 종속변수의 신뢰구간을 산출한다. ’prediction’은 회귀계수의 신뢰구간과 오차항으로 종속변수의 신뢰구간을 산출한다.

가상의 자료로 용법을 살펴보자.

newdata를 투입하지 않으면 회귀모형(2을 곱하는 모형)에 투입했던 값을 그대로 산출.

x <- 1:10
y <- x * 2
lm(y ~ x) -> fit
predict(fit)
##  1  2  3  4  5  6  7  8  9 10 
##  2  4  6  8 10 12 14 16 18 20

newdata를 투입해보자. 새로운 값에 회귀모형(2씩 곱하기)을 적용한 값을 산출한다. newdata =인자에는 데이터프레임으로 투입하는데, 이때 열의 이름이 독립변수의 열 이름과 같아야 한다.

new_df <- data.frame(x = c(2, 2, 2, 3, 3, 3, 20))
predict(fit, newdata = new_df)
##  1  2  3  4  5  6  7 
##  4  4  4  6  6  6 40

interval을 신뢰구간으로 설정해보자. 오차항이 없는 회귀식이므로 구간과 적합예측값이 동일하다.

predict(fit, interval = 'confidence', newdata = new_df)
##   fit lwr upr
## 1   4   4   4
## 2   4   4   4
## 3   4   4   4
## 4   6   6   6
## 5   6   6   6
## 6   6   6   6
## 7  40  40  40

오차항을 투입한 회귀모형으로 신뢰구간을 예측해보자.

x <- 1:10
y <- x * 2 + rnorm(10, 10, 1)
lm(y ~ x) -> fit
predict(fit, interval = 'confidence', newdata = new_df)
##        fit      lwr      upr
## 1 14.65364 13.65300 15.65429
## 2 14.65364 13.65300 15.65429
## 3 14.65364 13.65300 15.65429
## 4 16.59792 15.75636 17.43949
## 5 16.59792 15.75636 17.43949
## 6 16.59792 15.75636 17.43949
## 7 49.65068 46.38383 52.91753

표준오차를 포함해 예측값을 구해보자

x <- 1:10
y <- x * 2 + rnorm(10, 10, 1)
lm(y ~ x) -> fit
predict(fit, 
        interval = 'confidence', 
        se.fit = T,
        newdata = new_df)
## $fit
##        fit      lwr      upr
## 1 14.31331 12.65836 15.96825
## 2 14.31331 12.65836 15.96825
## 3 14.31331 12.65836 15.96825
## 4 16.20572 14.81388 17.59757
## 5 16.20572 14.81388 17.59757
## 6 16.20572 14.81388 17.59757
## 7 48.37685 42.97388 53.77982
## 
## $se.fit
##         1         2         3         4         5         6         7 
## 0.7176682 0.7176682 0.7176682 0.6035743 0.6035743 0.6035743 2.3430010 
## 
## $df
## [1] 8
## 
## $residual.scale
## [1] 1.439706

9.3.2 득표율 임계치에서 예측

노동당 임계치 당선자와 낙선자의 순자산 신뢰구간을 구하자. 당선과 낙선을 구분하는 기준점이 득표율 0인 지점이므로, newdata에는 값이 0인 데이터프레임을 만들어 투입한다.

# 당선자 순자산 신뢰구간
pred_labour1 <-
df %>% 
  filter.(party == "labour" & margin > 0) %>%  # 노동당 당선자 부분선택
  lm(ln.net ~ margin, .) %>%                   # 회귀모형
  predict(interval = 'confidence', se.fit = T, # 신뢰구간과 표준오차 예측
          newdata = tidytable(margin = 0))     # 당락구분값인 0으로 예측
pred_labour1
## $fit
##       fit      lwr      upr
## 1 11.9356 11.42013 12.45106
## 
## $se.fit
## [1] 0.256996
## 
## $df
## [1] 53
## 
## $residual.scale
## [1] 1.247931
# 낙선자 순자산 신뢰구간
pred_labour0 <- 
df %>% 
  filter.(party == "labour" & margin < 0) %>% 
  lm(ln.net ~ margin, .) %>% 
  predict(interval = 'confidence', se.fit = T,
          newdata = tidytable(margin = 0))
pred_labour0
## $fit
##        fit      lwr      upr
## 1 12.30367 12.02913 12.57821
## 
## $se.fit
## [1] 0.1389193
## 
## $df
## [1] 147
## 
## $residual.scale
## [1] 0.9075171

predict()함수로 얻은 표준오차는 lm()함수를 요약출력해 얻은 절편의 표준오차와 같다. 0인 값으로 예측한 값은 회귀모형의 추정절편과 같기 때문이다.

# 당선자 회귀모형의 절편의 표준오차
df %>% 
  filter.(party == "labour" & margin > 0) %>% 
  lm(ln.net ~ margin, .) %>% tidy() %>% select.(term, std.error) %>% 
# 당선자 예측값의 표준오차와 열 결합
  bind_cols.(
    data.frame(단절지점SE = c(pred_labour1$se.fit, NA))
  ) %>% gt() %>% 
  tab_header("당선자 회귀모형 절편값과 당선임계치 예측 표준오차")
당선자 회귀모형 절편값과 당선임계치 예측 표준오차
term std.error 단절지점SE
(Intercept) 0.256996 0.256996
margin 2.337382 NA
 
# 낙선자 회귀모형의 절편의 표준오차
df %>% 
  filter.(party == "labour" & margin < 0) %>% 
  lm(ln.net ~ margin, .) %>% tidy() %>% select.(term, std.error) %>% 
# 낙선자 예측값의 표준오차와 열 결합
  bind_cols.(
    data.frame(단절지점SE = c(pred_labour0$se.fit, NA))
  ) %>% gt() %>% 
  tab_header("낙선자 회귀모형 절편값과 당선임계치 예측 표준오차")
낙선자 회귀모형 절편값과 당선임계치 예측 표준오차
term std.error 단절지점SE
(Intercept) 0.1389193 0.1389193
margin 1.1019573 NA

당선자와 낙선자의 0으로 예측한 예측값의 표준오차의 차이를 계산하면, 임계치로 당선한 사람과 낙선한 사람의 순자산 차이를 비교할 수 있게 된다.

따라서, 앞서 토리당 의원의 당선이전 자산과 당선이후의 자산이 같다는 영가설은 당선임계치로 예측한 표준오차의 차이를 계산함으로써 검정할 수 있다.

회귀단절모형(RDD)으로 인과추론을 할 수 있는 이유는 두 예측값의 차이가 추정 평균처치효과(ATE: average treatment effect)를 나타내기 때문이다. 게다가, 임계값으로 예측한 두 표준오차는 독립적인 것으로 간주한다. 두개의 개별 측정값 집합으로 적합해 산출한 두개의 회귀모형에 기반하기 때문이다. 이는 두 예측값 차이의 분산이 두 예측값 분산의 합임을 의미한다(Imai 2018).

다음공식을 통해 추청된 차이에 대한 표준오차를 구할 수 있다.

\[ (\widehat{Y_1} - \widehat{Y_0}) 표준오차 = \sqrt{(\widehat{Y_1} 표준오차)^2 + (\widehat{Y_0} 표준오차)^2} \]

se_diff <- sqrt(pred_labour0$se.fit^2 + pred_labour1$se.fit^2)
se_diff
## [1] 0.2921395

차이의 표준오차를 구했으므로, 차이의 점추정치에 대한 신뢰구간을 구할 수 있다.

차이의 점추정치는 다음과 같다.

diff_est <- 
pred_labour1$fit[1, "fit"] - pred_labour0$fit[1, "fit"]
diff_est
## [1] -0.3680728

차이의 표준오차로 점추정치의 95%수준의 신뢰구간을 구하면 다음과 같다. 양측으로 0.025만큼의 확률면적을 빼야 하므로 신뢰구간의 상한과 하한에 각각 0.975에 해당하는 면적만큼 표준오차를 곱한다.

ci_labour <- c(diff_est - se_diff * qnorm(0.975), 
             # 0.025로 계산하면 하한값 산출하므로 덧셈
             # diff_est + se_diff * qnorm(0.025), 
               diff_est + se_diff * qnorm(0.975))
ci_labour
## [1] -0.9406558  0.2045102
  • qnorm()은 pnorm()의 역수. 누적분포값 p를 투입하면, x축의 값(p까지의 면적에 해당하는값)을 산출한다.
qnorm(p = 0.975, mean = 0, sd = 1, lower.tail = T)
## [1] 1.959964

점추정치의 표준화점수(예측값 차이 / 표준오차)를 이용해, pnorm()함수로 표준정규분포상의 유의확률 \(p\)값을 계산한다. 차이에 대한 검정이므로 양측검정이다. 유의확률은 영가설이 참일 때 발생가능성이 낮은 정도를 나타내므로, lower.tail은 FALSE로 지정한다.

pnorm(abs(diff_est/se_diff), lower.tail = F) * 2
## [1] 0.2076978
  • pnorm()은 x축의 값이 q일때, q까지의 면적에 해당하는 확률 p를 산출한다.
pnorm(1.26, lower.tail = F)
## [1] 0.1038347

신뢰구간(95%CI[-0.94, 0.20])에 0이 포함돼 있고, \(p\)값 0.21이 유의수준 0.05보다 크기 때문에 노동당은 의원의 당선 전후의 자산이 동일하다는 영가설을 기각하지 않고 유지한다. 즉, 이 자료는 노동당 의원의 자산증가는 의원직 당선과 관련성이 있다는 근거가 되지 않는다.

9.3.3 토리당의 단절 가설검정

토리당 의원의 의원직 당선과 자산증가의 관계에 대해 분석해보자.

먼저 낙선과 당선 단절지점을 구분한다.

df %>% 
  mutate.(margin0 = ifelse(margin < 0, margin, 0),
          margin1 = ifelse(margin > 0, margin, 0),
          D = ifelse(margin > 0, 1, 0)) %>% 
  filter.(party == "tory") %>% 
ggplot(aes(margin, ln.net, color = factor(D))) +
  geom_point(alpha = .3) +
  geom_smooth(
    aes(margin0, ln.net), method = 'lm') +
  geom_smooth(
    aes(margin1, ln.net), method = 'lm') +
  labs(title = "토리당의 득표율과 순자산 관계: 단절구분")
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'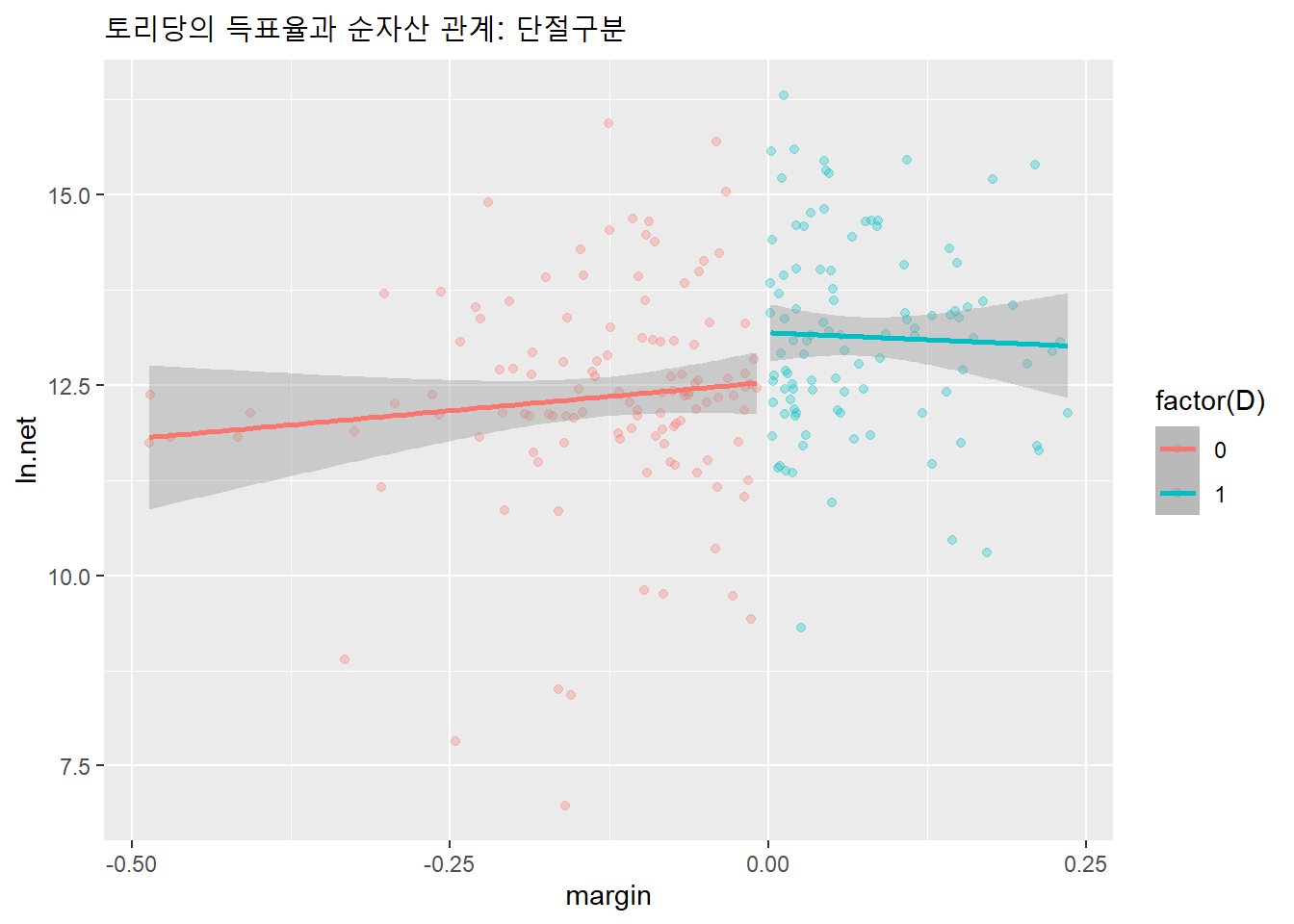

토리당 임계치 당선자와 낙선자의 순자산 신뢰구간을 구한다.

# 당선자 순자산 신뢰구간
pred_tory1 <-
df %>% filter.(party == "tory" & margin > 0) %>% 
  lm(ln.net ~ margin, .) %>% 
  predict(interval = 'confidence', se.fit = T,
          newdata = tidytable(margin = 0))
pred_tory1
## $fit
##       fit      lwr      upr
## 1 13.1878 12.80691 13.56869
## 
## $se.fit
## [1] 0.1919821
## 
## $df
## [1] 100
## 
## $residual.scale
## [1] 1.288785
# 낙선자 순자산 신뢰구간
pred_tory0 <- 
df %>% filter.(party == "tory" & margin < 0) %>% 
  lm(ln.net ~ margin, .) %>% 
  predict(interval = 'confidence', se.fit = T,
          newdata = tidytable(margin = 0))
pred_tory0
## $fit
##        fit      lwr      upr
## 1 12.53812 12.11402 12.96221
## 
## $se.fit
## [1] 0.2141793
## 
## $df
## [1] 119
## 
## $residual.scale
## [1] 1.434283

당선자와 낙선자 자산 차이의 표준오차를 구한다.

se_diff <- sqrt(pred_tory0$se.fit^2 + pred_tory1$se.fit^2)
se_diff
## [1] 0.2876281

자산 차이에 대한 점추정치를 구한다.

# 자산 차이의 점추정치
diff_est <- 
pred_tory1$fit[1, "fit"] - pred_tory0$fit[1, "fit"]
diff_est
## [1] 0.6496861

점추정치와 표준오차를 이용해 95% 수준 신뢰구간을 계산한다.

# 자산 차이 추정치의 신뢰구간
ci_tory <- c(diff_est - se_diff * qnorm(0.975), diff_est + se_diff * qnorm(0.975))
ci_tory
## [1] 0.0859455 1.2134268

점추정치의 표준화점수로 영가설이 참인경우의 유의확률 \(p\)값을 계산할 수 있다.

pnorm(abs(diff_est/se_diff), lower.tail = F) * 2
## [1] 0.02389759

신뢰구간(95%CI[0.09, 1.21])에 0이 포함돼 있지 않고, \(p\)값 0.023이 유의수준 0.05보다 작기 때문에 토리당은 의원의 당선 전후의 자산이 동일하다는 영가설을 기각하고 대안가설을 채택한다. 즉, 이 자료는 토리당 의원의 자산증가는 의원직 당선과 관련성이 있다는 근거가 된다.

9.3.4 회귀단절설계 가설검정 방법

  • 연구가설 및 영가설 설정
  • 예비분석: 기술통계 및 선형회귀분석
  • 단절지점 지정해 산점도와 회귀선 시각화
  • 단절지점 전과 후로 부분선택(df1, df0)해 각각 단절지점으로 예측한 신뢰구간과 표준오차 산출(pred1, pred2)
fit <- lm(y ~ x, df1)
predict(fit, interval = 'confidence', se.fit = T, newdata = tidytable(cols = 0))
pred1
fit <- lm(y ~ x, df0)
predict(fit, interval = 'confidence', se.fit = T, newdata = tidytable(cols = 0))
pred0
  • 단절지점으로 예측한 종속변수 차이의 표준오차 계산
  se_diff <- sqrt(pred1$se.fit^2 + pred0$se.fit^2)
  • 단절지점으로 예측한 종속변수 차이의 점추정치 계산
  diff_est <- pred1$fit[1, "fit"] - pred0$fit[1, "fit"]
  • 점추정치와 표준오차를 이용해 차이의 신뢰구간 계산(예: 95%신뢰수준)
  diff_est - se_diff * qnorm(0.975)
  diff_est + se_diff * qnorm(0.975)
  • 점추정치와 표준오차를 이용해 유의확률 계산
  pnorm(abs(diff_est/se_diff), lower.tail = F) * 2

9.4 종합

9.4.1 통계

  • 회귀단절설계(RDD: regression discontinuity design)
  • 무작위통제시험(RCT: randomized controlled trial)
  • 표준화점수(z-score)
  • 로그변환
  • 로그
  • 지수
  • 자연로그
  • 상용로그

9.4.2 코딩

  • rnorm()
  • dnorm()
  • pnorm()
  • qnorm()
  • ggplot
    • stat_function()
    • geom_dotplot()
    • geom_area()
    • geom_rect()
    • annotate()
    • geom_hline()
    • geom_vline()
  • log()
  • log10()
  • log2()
  • exp()
  • predict()

References

Eggers, Andrew C, and Jens Hainmueller. 2009. “MPs for Sale? Returns to Office in Postwar British Politics.” American Political Science Review 103 (4): 513–33.
Imai, Kosuke. 2018. Quantitative Social Science: An Introduction. Princeton University Press.