10 모형진단과 교정

c("ggplot2movies", "regclass", "moderndive",
  "rio", "tidyverse", "tidytable", 
  "psych", "psychTools", "car", "caret",
  "skimr", "janitor", "tidymodels", "lm.beta", "mediation", 
  "GGally", "ggforce", "mdthemes", "patchwork", "ggdag",
  "r2symbols", "equatiomatic", "gt", "ggpubr", "ggfortify" 
  ) -> pkg 
sapply(pkg, function(x){
  if(!require(x, ch = T)) install.packages(x, dependencies = T)
  library(x, ch = T)
})

추론통계는 모형을 이용해 자료를 분석해 정보를 산출함으로써 모수를 추론한다. 통계적 유의성은 이 과정의 불확실성을 정량화함으로써 오류가능성을 통제 범위 안에 둔다. 유의수준 0.05라면 오류가능성 5%를 수용할 만한 불확실성으로 판단하는 것이다.

비록 통계적 유의성을 이용해 불확실성을 정량화함으로써 가설검정 과정의 오류 가능성을 통제범위 안에 둘 수 있도록 하나, 통계적 유의성 만으로는 오류가능성을 모두 회피할 수 없다. 표본이 독특한 특성을 지니고 있어 수집한 자료가 통계모형의 전제를 충족하지 않거나 선택한 모형이 자료와 전혀 부합하지 않는다면 분석결과는 신뢰할 수 없게 된다.

따라서 가설검정과 신뢰구간에 대한 분석결과의 타당성과 신뢰성을 확보하기 위해서는 추론의 전제를 충족하는지 점검해 문제가 발생하면 모형을 교정해야 한다. 이를 위해 회귀분석을 중심으로 모형진단과 교정방법에 대해 학습한다.

10.1 모형진단

선형회귀를 이용한 추론은 LINE으로 요약할 수 있는 4개 조건을 충족해야 한다.

• 선형성(Linearity): 변수 사이의 선형성
• 독립성(Independence): 잔차의 독립성
• 정규성(Normality): 잔차의 정규성
• 등분산성(Equality of variance): 잔차의 등분산성
  • 등분산성은 Homoscedasticity라고 한다.

선형성, 정규성, 등분산성은 잔차를 분석해 확인할 수 있다. 독립성은 표집방법에 의해 결정된다.

10.1.1 LINE

회귀모형에서 잔차(residual: 오차항의 설명량)는 종속변수에 대해 모형으로 투입한 독립변수들로 설명되지 않고 남은 나머지 부분이다. 분석에 포함되지 않았지만, 종속변수에 영향을 미치는 미지의 변수들이다.

먼저 moderndive패키지의 evals데이터셋으로 잔차에 대해 복습하자.

• 잔차에 대해서는 [4.1 선형회귀의 4.1.2 잔차](https://codingstat.netlify.app/week4.html#%EC%84%A0%ED%98%95%ED%9A%8C%EA%B7%80)에 설명돼 있다.

evals는 미국 텍스트대학교(오스틴)의 강의평가에 대한 설문조사 결과다. 463개 과목의 교수 94명에 대한 강의평가와 점수와 관련 변수가 포함돼 있다.

names(evals)

##  [1] "ID"           "prof_ID"      "score"        "age"          "bty_avg"     
##  [6] "gender"       "ethnicity"    "language"     "rank"         "pic_outfit"  
## [11] "pic_color"    "cls_did_eval" "cls_students" "cls_level"

이중 분석에 사용할 변수는 다음과 같다.

evals %>%
  select.(ID, prof_ID, score, bty_avg) %>% 
  glimpse()

## Rows: 463
## Columns: 4
## $ ID      <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18,~
## $ prof_ID <int> 1, 1, 1, 1, 2, 2, 2, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5,~
## $ score   <dbl> 4.7, 4.1, 3.9, 4.8, 4.6, 4.3, 2.8, 4.1, 3.4, 4.5, 3.8, 4.5, 4.~
## $ bty_avg <dbl> 5.000, 5.000, 5.000, 5.000, 3.000, 3.000, 3.000, 3.333, 3.333,~

• ID: 과목 식별번호
• prof_ID: 교수 식별번호
• score: 강의평가 점수: (1) very unsatisfactory - (5) excellent.
• bty_avg: 교수의 미모에 대한 점수 평균

회귀모형에서 측정값, 예측값, 잔차를 구하면 다음과 같다.

evals %>% 
  lm(score ~ bty_avg, data = .) %>% augment() %>% 
  sample_n(5) %>%  # 5개열만 무작위 추출
  gt() %>% 
  tab_header("측정값, 예측값, 잔차: 5개 무작위 추출") %>% 
  fmt_number(-1, decimals = 2)

측정값, 예측값, 잔차: 5개 무작위 추출
score	bty_avg	.fitted	.resid	.hat	.sigma	.cooksd	.std.resid
4.3	3.33	4.10	0.20	0.00	0.54	0.00	0.37
4.1	7.83	4.40	−0.30	0.01	0.54	0.00	−0.57
3.6	2.83	4.07	−0.47	0.00	0.53	0.00	−0.88
4.5	6.83	4.34	0.16	0.01	0.54	0.00	0.31
4.5	4.33	4.17	0.33	0.00	0.54	0.00	0.62

• score: 종속변수 측정값
• bty_ave: 독립변수 측정값
• .fitted: 예측값 또는 적합값
• .resid : 잔차(residual). 측정값과 적합값의 차이(오차: error)

측정값을 산점도에 표시하고 적합값을 회귀선으로 표시하면 다음과 같다. 이중 측정값 하나(적색)를 선택해 적합값과의 거리(잔차: 초록)를 나타냈다.

evals %>% 
  lm(score ~ bty_avg, data = .) %>% augment() %>% 
ggplot(aes(x = bty_avg, y = score)) +
  geom_point(alpha = .5) +
  # 측정값과 적합값 연결선
  geom_segment(aes(x = score[1], xend = score[1],
                   y = bty_avg[1], yend = .fitted[1]),
               color = 'green', size = 2) +
  # 측정값 점
  geom_point(aes(x = score[1], y = bty_avg[1]), 
             color = 'red', size = 6) +
  geom_smooth(method = lm, se = FALSE, size = 3) + 
  labs(x = "미모 점수", 
       y = "강의 점수",
       title = "강의와 미모 점수의 관계 및 한 측정값의 잔차")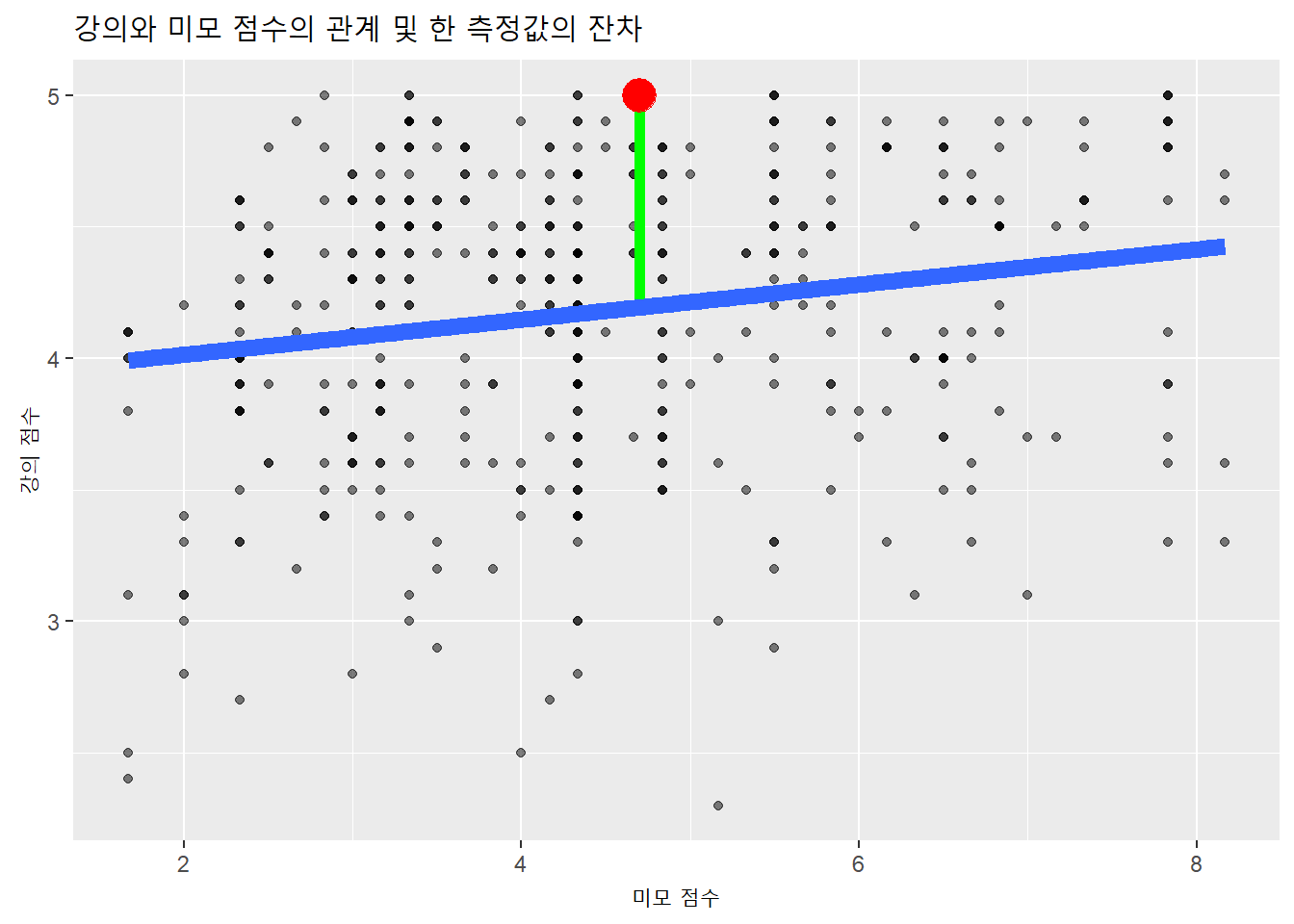 

10.1.1.1 L: 선형성

위 산점도를 보면 강의평가자료의 독립변수와 종속변수의 관계에 대해 확실하지는 않아도 선형성이 나타난다고 판단할 수 있다.

비선형관계는 아래처럼 U자형의 다항(polynomial) 곡선의 분포가 나타나는 경우다.

evals %>% 
  mutate.(score2 = scale(bty_avg)^2 + score) %>% 
ggplot(aes(x = bty_avg, y = score2)) +
  geom_point(alpha = .4) +
  geom_smooth(method = lm, se = FALSE, size = 3) +
  labs(x = "독립변수", 
       y = "종속변수",
       title = "비선형 관계 가상 사례")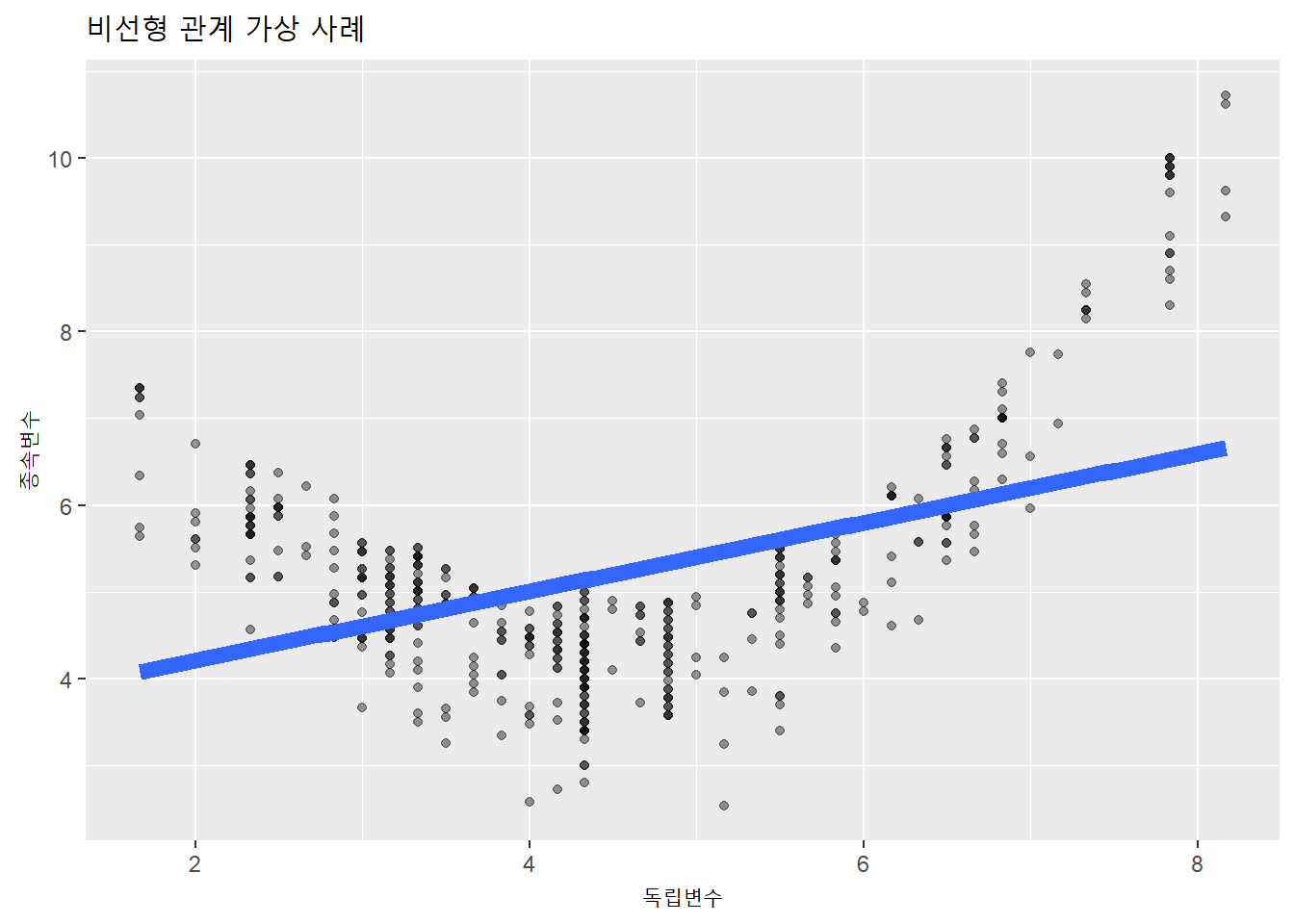

잔차를 종속변수로 투입하면, 기울기가 0인 산점도와 회귀선이 생성된다. 적합값(예측값)과 측정값의 차이가 잔차이기 때문이다.

evals %>% 
  mutate.(score2 = scale(bty_avg)^2 + score) %>% 
  lm(score2 ~ bty_avg, .) %>% augment() %>% 
ggplot(aes(x = bty_avg, y = .resid)) +
  geom_point(alpha = .4) +
  geom_smooth(method = lm, se = FALSE, size = 3, 
              color = 'dodgerBlue') +
  labs(x = "독립변수", 
       y = "잔차",
       title = "비선형 관계 가상 사례")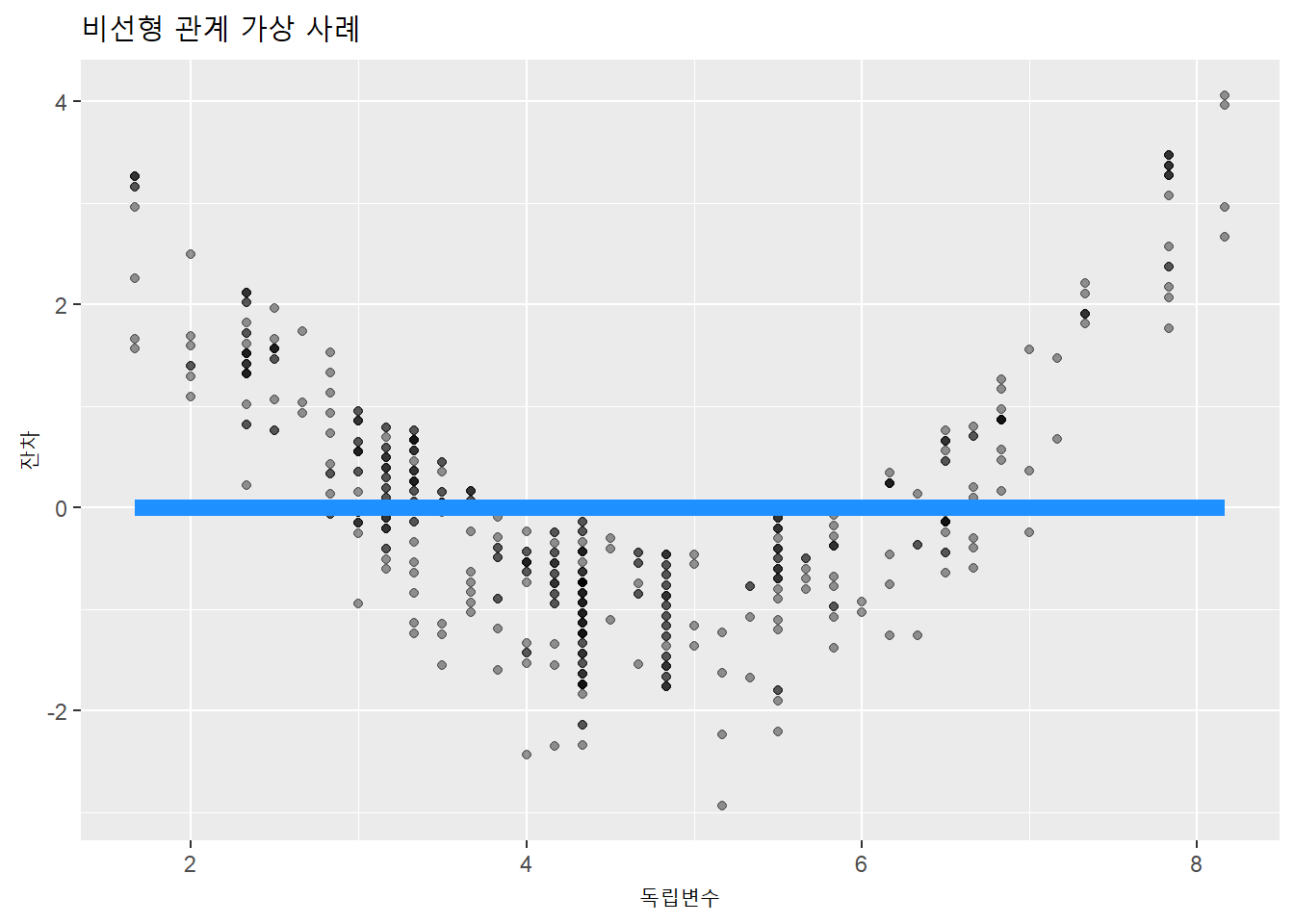

비선형관계가 확인되면 선형회귀모형이 아닌 비선형 관계를 다룰 수 있는 모형을 이용해야 한다. 비선형 회귀모형은 고급통계에서 다룬다.

10.1.1.2 I: 독립성

선형회귀의 두번째 조건은 관측값의 상호 독립성이다. 텍사스대 강의평가 자료의 463개 강좌는 교수 94명이 담당했다. 즉, 같은 교수가 두번 이상 반복측정됐다. 교수ID 1번은 4회, 2번은 3회 측정됐다. 같은 대상이 반복돼 측정됐으므로 측정의 독립성이 충족되지 않는다.

evals %>% head(10)

## # A tibble: 10 x 14
##       ID prof_ID score   age bty_avg gender ethnicity  language rank  pic_outfit
##    <int>   <int> <dbl> <int>   <dbl> <fct>  <fct>      <fct>    <fct> <fct>     
##  1     1       1   4.7    36    5    female minority   english  tenu~ not formal
##  2     2       1   4.1    36    5    female minority   english  tenu~ not formal
##  3     3       1   3.9    36    5    female minority   english  tenu~ not formal
##  4     4       1   4.8    36    5    female minority   english  tenu~ not formal
##  5     5       2   4.6    59    3    male   not minor~ english  tenu~ not formal
##  6     6       2   4.3    59    3    male   not minor~ english  tenu~ not formal
##  7     7       2   2.8    59    3    male   not minor~ english  tenu~ not formal
##  8     8       3   4.1    51    3.33 male   not minor~ english  tenu~ not formal
##  9     9       3   3.4    51    3.33 male   not minor~ english  tenu~ not formal
## 10    10       4   4.5    40    3.17 female not minor~ english  tenu~ not formal
## # ... with 4 more variables: pic_color <fct>, cls_did_eval <int>,
## #   cls_students <int>, cls_level <fct>

evals %>% 
  ggplot(aes(bty_avg, score)) +
  geom_jitter(aes(color = prof_ID == 15 | prof_ID == 5), 
              alpha = .8) +
  scale_color_manual(values = c('slategray', 'red')) +
  labs(x = "미모점수", 
       y = "강의평가",
       color = "교수ID: 5 & 15",
       title = "prof_ID의 반복측정값")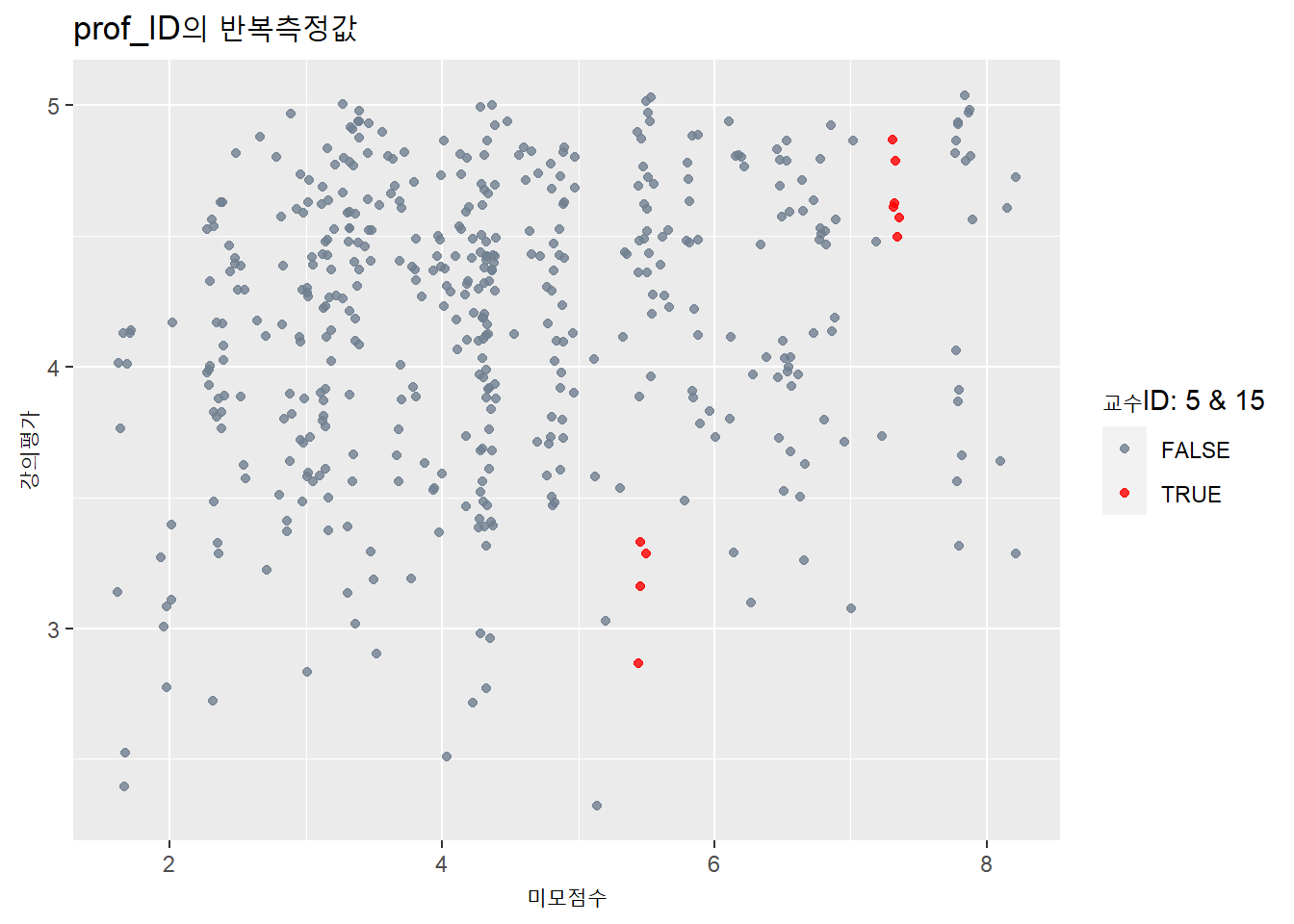

동일인물이 담당한 강의의 강의평가 점수는 비슷할 가능성이 높기 때문에, 이 데이터셋은 463명이 463개 강좌를 담당한 경우의 데이터셋과는 그 성격이 다르다.

같은 대상에 대해 반복적으로 측정했을 때 관측값 사이에 의존성이 있다고 한다. 이처럼 독립성의 전제를 충족하지 못하는 자료에 대해서는 반복측정의 영향을 계산할 수 있는 모형을 분석에 이용해야 한다.

10.1.1.3 N: 정규성

선형회귀의 세번째 조건은 잔차의 정규성이다. 잔차의 분포가 정규분포를 이뤄야 하고, 잔차 분포의 중심은 0이어야 한다. 잔차의 정규성은 잔차의 히스토그램을 통해 확인할 수 있다.

evals %>% 
  lm(score ~ bty_avg, .) %>% augment() %>% 
ggplot(aes(x = .resid)) +
  geom_histogram(binwidth = .25, color = 'deeppink') +
  labs(x = "잔차",
       title = "잔차의 히스토그램")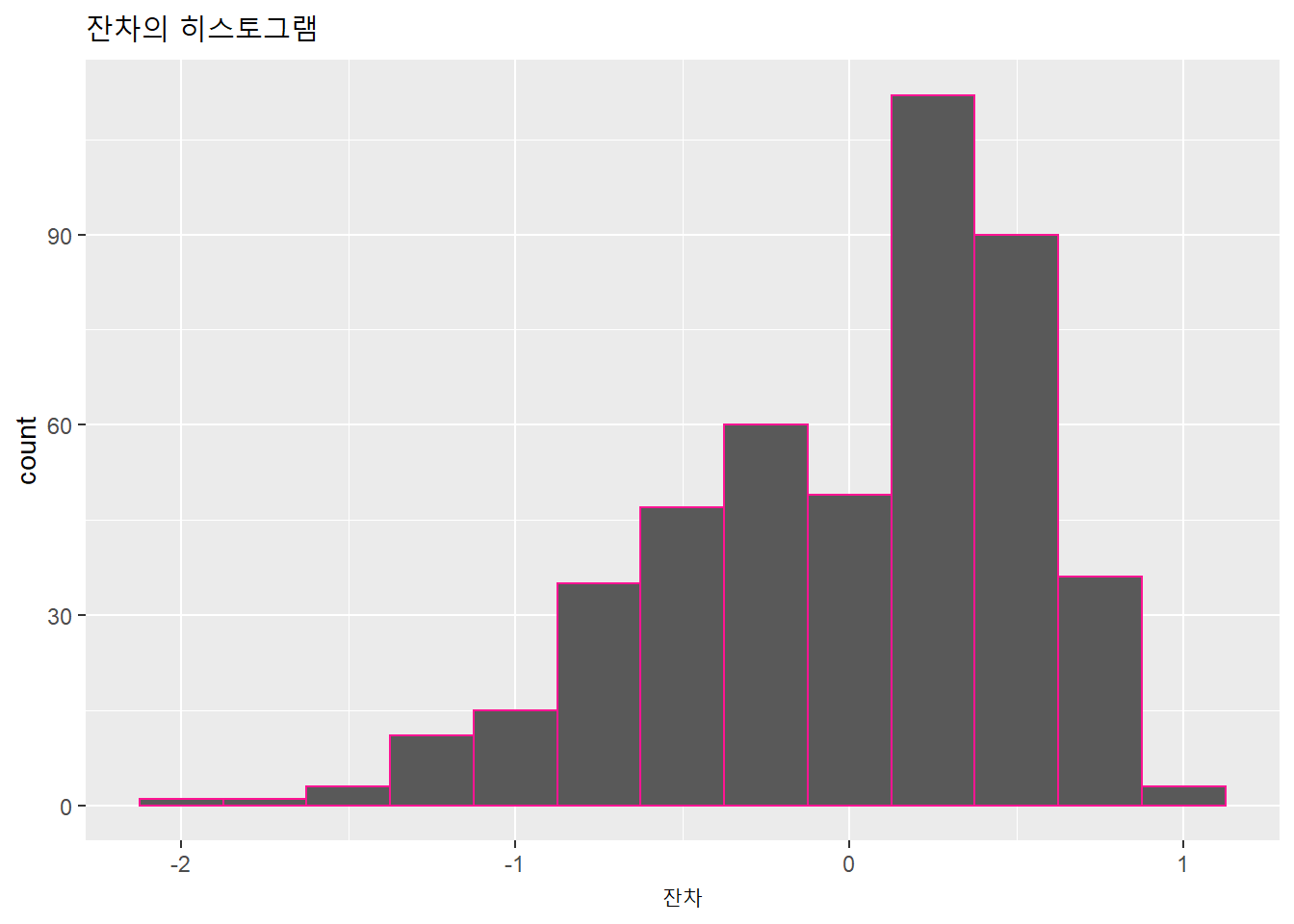

위 히스토그램에서는 양의 잔차가 음의 잔차보다 다소 많은 편이고, 왼쪽으로 다소 치우쳐 있다.

• 왜도(skewness): 한쪽으로 치우친 정도. 비대칭도라고도 한다. 꼬리가 있는 방향으로 치우쳤다고 한다. 왜도의 값이 양수이면 오른쪽이 꼬리, 음수이면 왼쪽으로 꼬리가 있는 분포다. 평균과 중앙값이 같으면 왜도는 0이 된다.

score를 psych패키지의 describe()함수로 왜도를 계산해보면 음수임을 알수 있다.

describe(evals$score) %>% select.(skew)

## # A tidytable: 1 x 1
##     skew
##    <dbl>
## 1 -0.697

10.1.1.3.1 Normal QQ plot

분포의 정규성은 Normal QQ plot을 통해 보다 명확하게 판단할수 있다.

• QQ plot의 Q는 quantile로서 나누는 지점(cutpoint)이다. 확률분포(probability distribution)를 동일한 확률 간격으로 나누는 결절점(cutpoints)이다.

• q-quantile은 q개의 동일한 간격으로 나눈 것이 된다. 예를 들어, 4개로 구분하면 4-quantile(= quartiles), 100개로 구분하면 100-quantile(= percentiles)가 된다.

# 0.5를 기준으로 2개의 q를 생성할 수 있는 cutpoints 산출
1:10 %>% quantile(x = ., probs = 1/2)

## 50% 
## 5.5

# 0.25, 0.5, 0.75를 기준으로 4개의 q를 생성할 수 있는 cutpoints 산출
1:10 %>% quantile(x = ., probs = c(1/4, 2/4, 3/4))

##  25%  50%  75% 
## 3.25 5.50 7.75

qnorm(p)함수로 산출하는 q가 quantile이다.

# 확률면적 0.95를 이루는 cutpoint 산출.
qnorm(0.95)

## [1] 1.644854

pnorm(q)은 cutpoint인 quantile을 투입해 확률면적 p 산출

pnorm(1.65)

## [1] 0.9505285

QQ plot은 두 변수의 확률분포에 대한 quantiles를 투입하여 두 변수의 분포를 비교하는 도표다. X축이 이론적인 정규분포이고, Y축이 측정값의 분포이다.

evals %>% 
ggplot(aes(sample = score)) +
  geom_qq_line(color = 'cornflowerblue', size = 2) +
  geom_qq(alpha = .4) + 
  labs(title = "강의점수에 대한 QQ plot",
       x = "이론적인 quantile",
       y = "측정값의 quantile")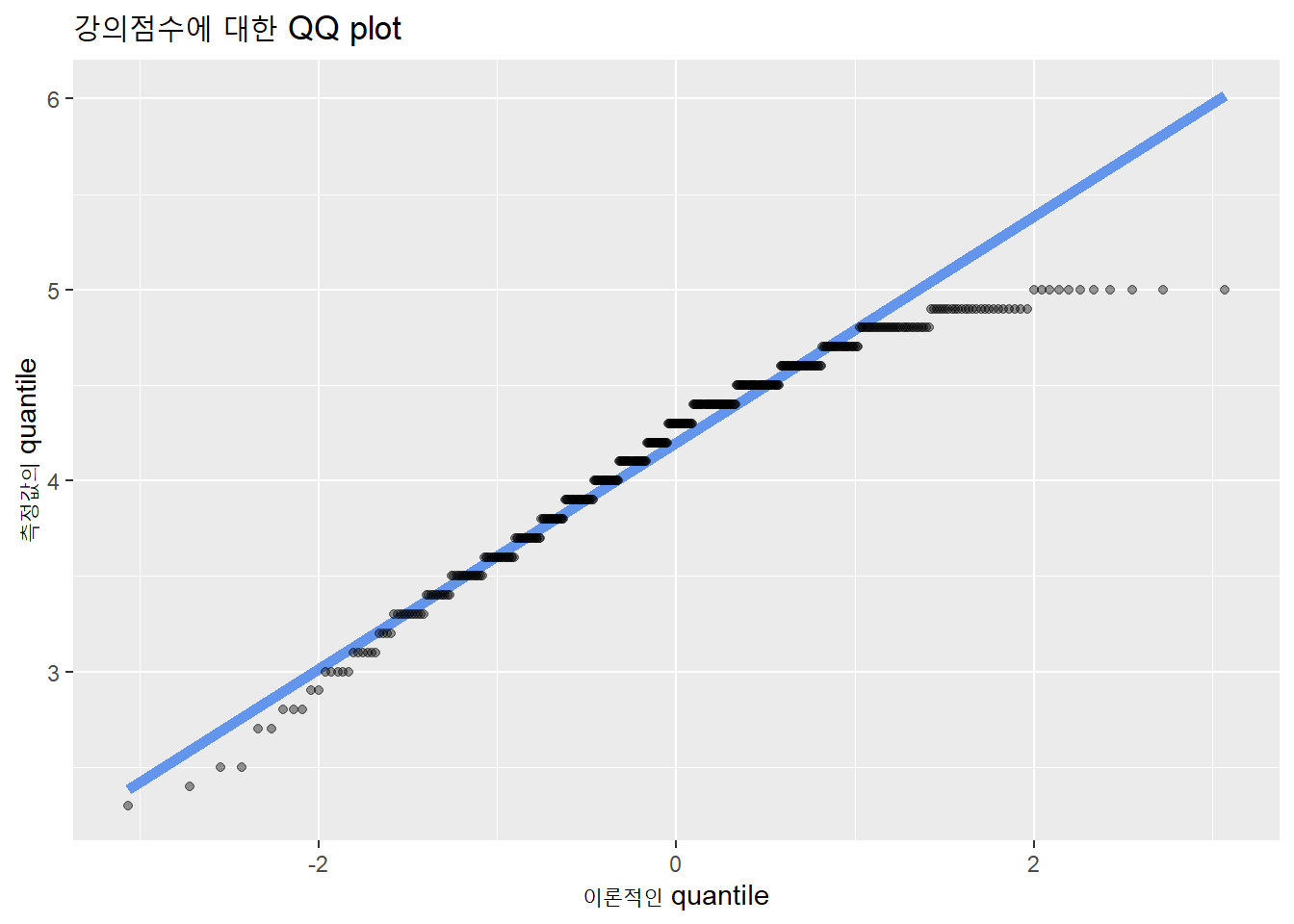

회귀모형의 잔차를 종속변수로 투입한 QQ plot은 다음과 같다.

evals %>% 
  lm(score ~ bty_avg, .) %>% augment() %>% 
ggplot(aes(sample = .resid)) +
  geom_qq_line(color = 'cornflowerblue', size = 2) +
  geom_qq(alpha = .4) + 
  labs(title = "잔차의 QQ plot: lm(score ~ bty_avg)",
       x = "이론적 quantile",
       y = "잔차의 quantile")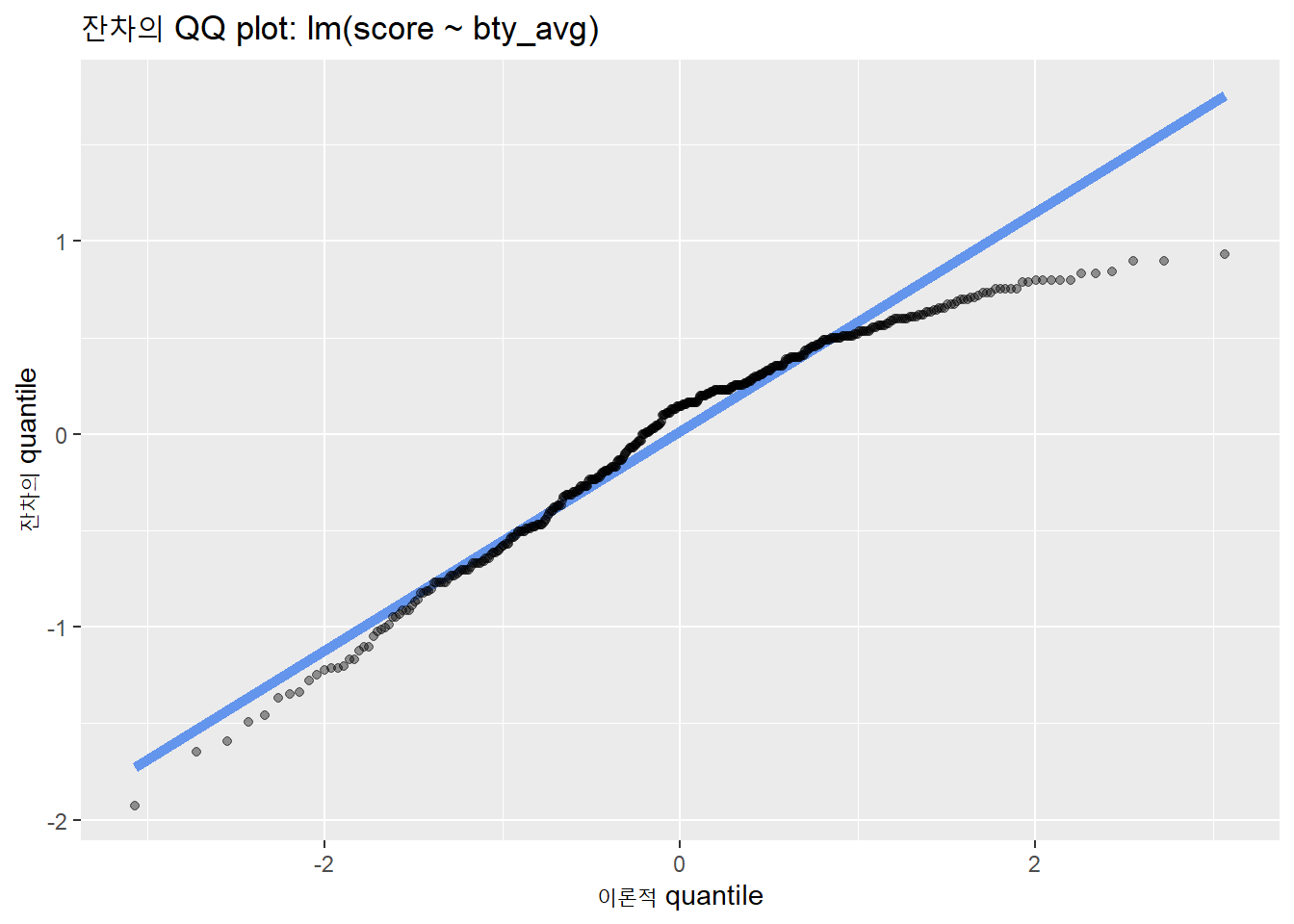 

히스토그램과 마찬가지로 오른쪽의 분포가 정규성에 어긋나 있다.

분포의 정규성 확인은 샤피로-윌크 검정(Shapiro-Wilk test)을 이용한다.

evals %>% 
  lm(score ~ bty_avg, .) %>% 
  augment() %>% pull(.resid) %>% # .resid열을 벡터로 추출
  shapiro.test()

## 
##  Shapiro-Wilk normality test
## 
## data:  .
## W = 0.95491, p-value = 1.089e-10

\(p\)값이 0.001보다 작아 유의수준 0.05에서 잔차의 정규성을 충족하지 못한다.

10.1.1.4 E: 등분산

선형회귀의 네번째 조건은 잔차의 등분산이다. 적합값과 잔차의 관계를 통해 확인할 수 있다. 등분산성은 오차가 일정하게 퍼져 있는 정도이기 때문에 오차분산의 일정성이라고도 한다.

• 등분산성은 homoscedasticity, 이분산성은 heteroscedasticity라고 한다.

등분산성이 있을 때는 아래와 같이 잔차와 예측값 사이에는 어떠한 체계적인 패턴이 나타나지 않는다.

evals %>% 
  lm(score ~ bty_avg, .) %>% augment() %>% 
ggplot(aes(x = .fitted, y = .resid)) +
  geom_point(alpha = .4) +
  geom_smooth(method = lm, se = FALSE, size = 3) +
  labs(x = "독립변수의 적합값", 
       y = "잔차",
       title = "잔차의 등분산")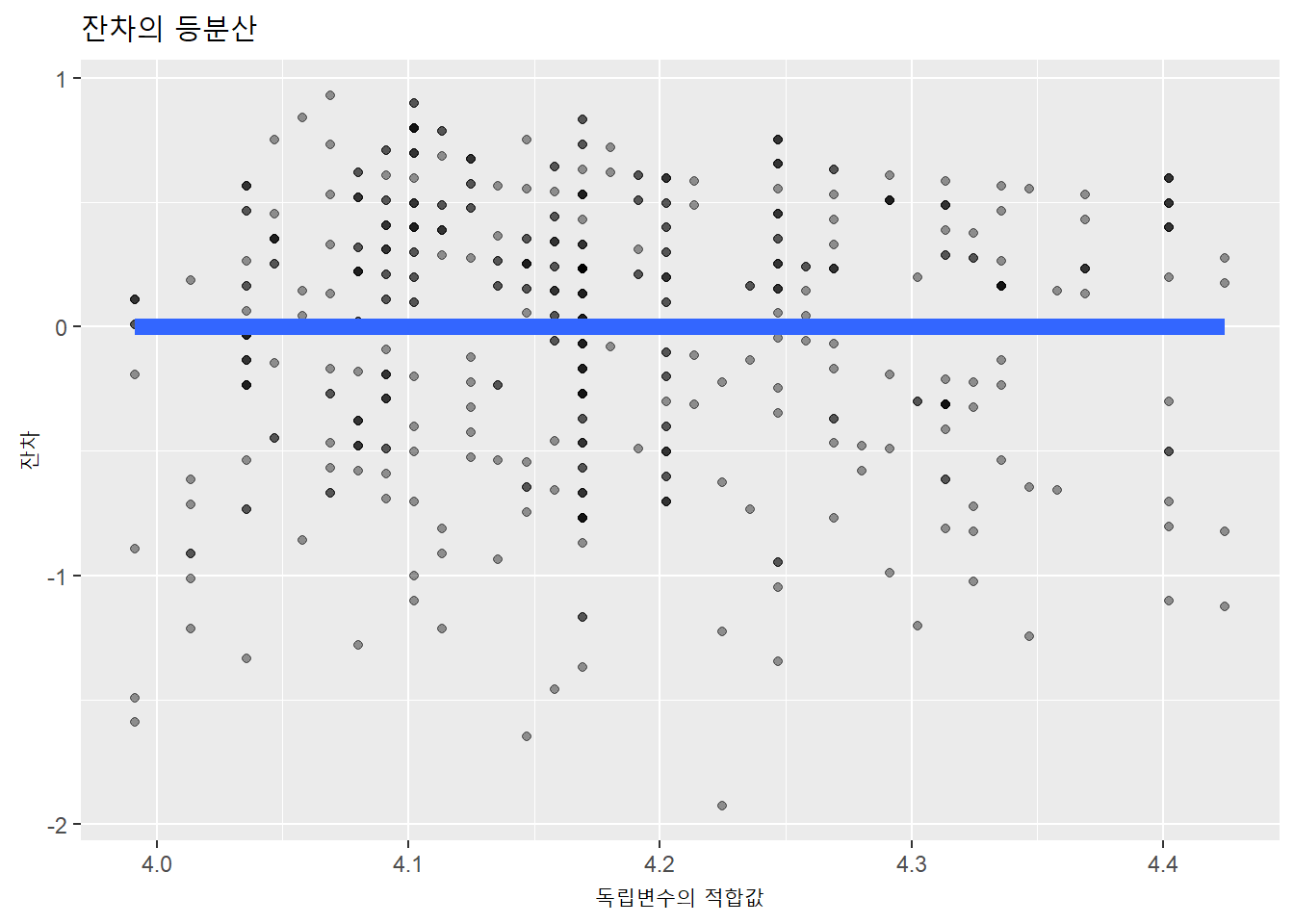

등분산성은 통계모형에서 가장 중요한 전제조건이다. 잔차(residual: 오차항의 설명량)는 종속변수에 대해 모형으로 투입한 독립변수들로 설명되지 않은 부분이다. 분석에 포함되지 않았지만, 종속변수에 영향을 미치는 미지의 변수들이다. 그런데, 잔차의 분산에 일정한 유형이 있다는 것은 모형에 포함돼야 하는 변수가 누락됐다는 의미가 된다.

아래 사례를 보자. 독립변수와 종속변수를 곱한 종속변수를 새로 만들어 잔차의 분산정도를 시각화했다.

오차의 분산이 일정하지 않고, 특정한 유형이 나타난다. 독립변수와 종속변수 사이에 분석 모형의 독립변수로 설명되지 않은 체계적인 변수가 누락돼 있기 때문이다.

잔차의 분산이 일정하지 않은 경우, 분석 모형에 새로운 독립변수를 추가한다.

evals %>% 
  mutate.(score2 = bty_avg * score) %>% 
  lm(score2 ~ bty_avg, .) %>% augment() %>% 
ggplot(aes(x = bty_avg, y = .resid)) +
  geom_point(alpha = .4) +
  geom_smooth(method = lm, se = FALSE, size = 3) +
  labs(x = "독립변수", 
       y = "잔차",
       title = "잔차의 이분산")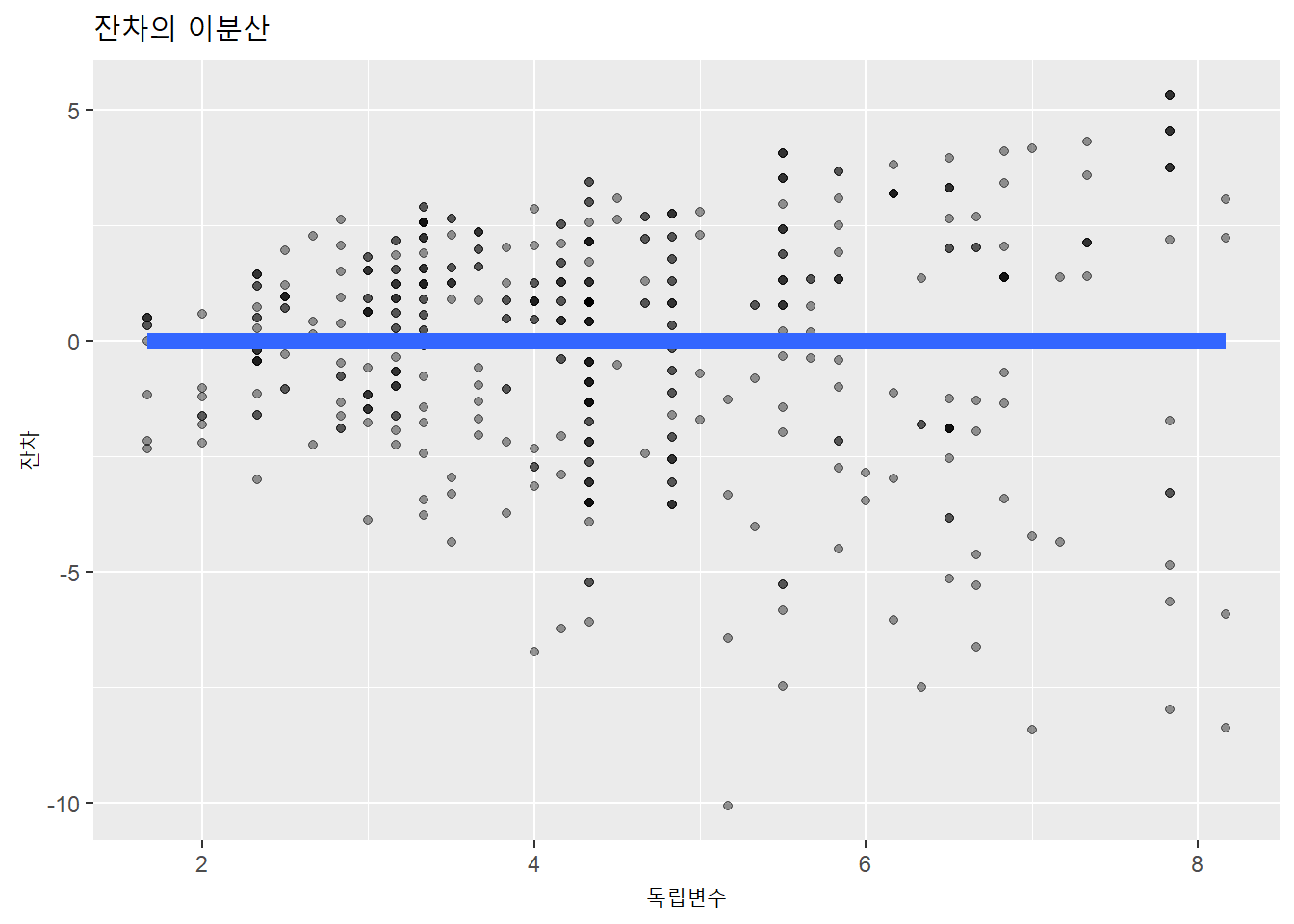

모형진단은 적합값에 대해 R기본함수인 plot() 혹은 ggfortify패키지의 autoplot()함수를 이용하면 간단하게 진단할 수 있다.

evals %>% 
  lm(score ~ bty_avg, .) %>% 
  autoplot(alpha = .4, label.size = 3)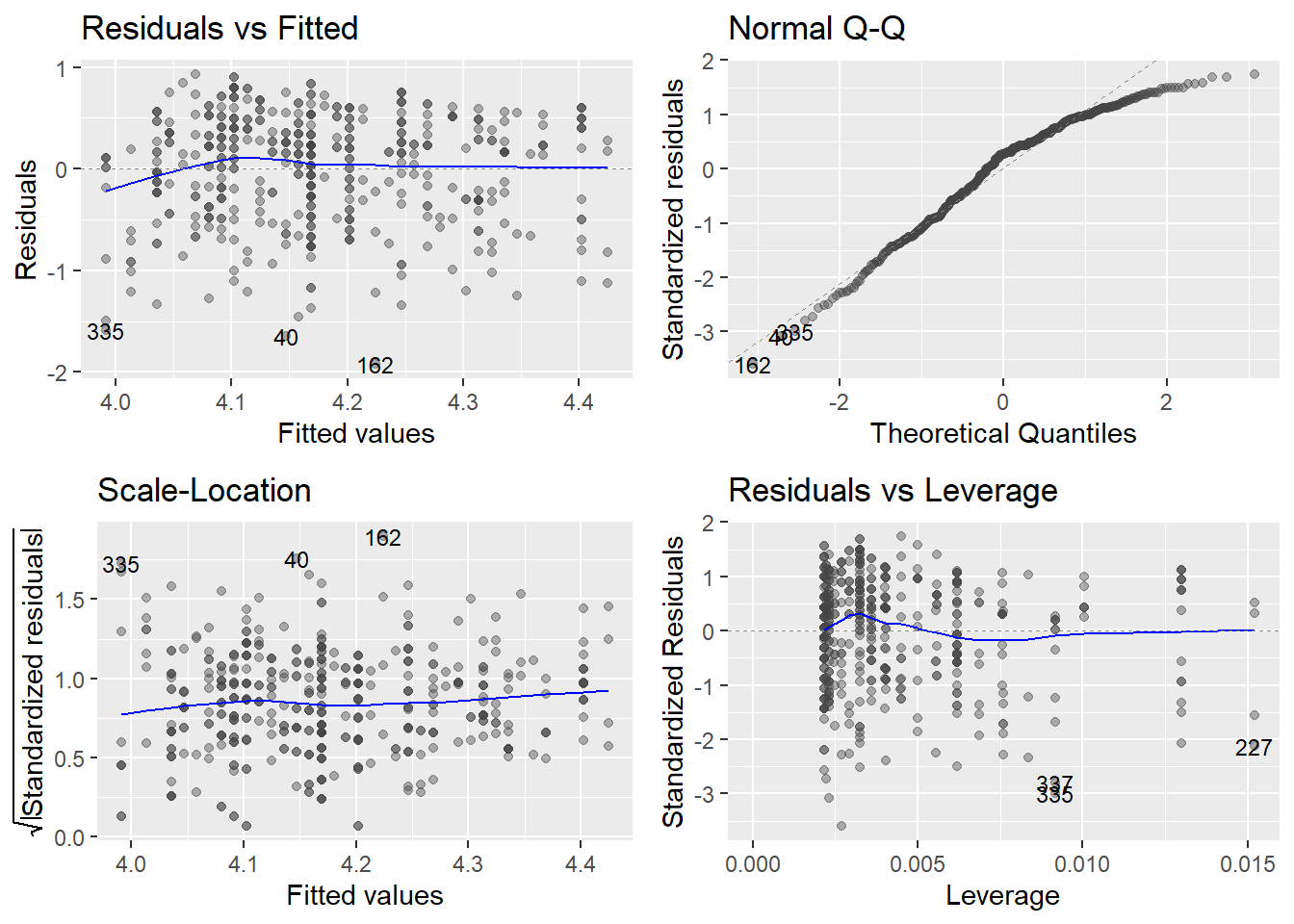 

• Residuals vs Fitted(왼쪽 위):
  • 선형성(Linearity): 변수 사이의 선형성
  • 잔차가 수평에 가까우면 대체로 선형성 충족.
• Normal Q-Q(오른쪽 위):
  • 정규성(Normality): 잔차의 정규성
  • 점의 분포가 선에 가까우면 대체로 정규성 충족
• Scale-Location(왼쪽 아래):
  • 등분산성(Equality of variance): 잔차의 등분산성
  • 수평선 주위의 분포가 무작위에 가까우면 대체로 등분산성 충족.

(독립성(Independence)은 표집방법으로 판단한다.)

autoplot()은 모두 6개의 도표를 제공하는데, 6개를 모두 보려면 which = 인자로 설정한다.

evals %>% 
  lm(score ~ bty_avg, .) %>% 
  autoplot(alpha = .4, label.size = 3, which = 1:6)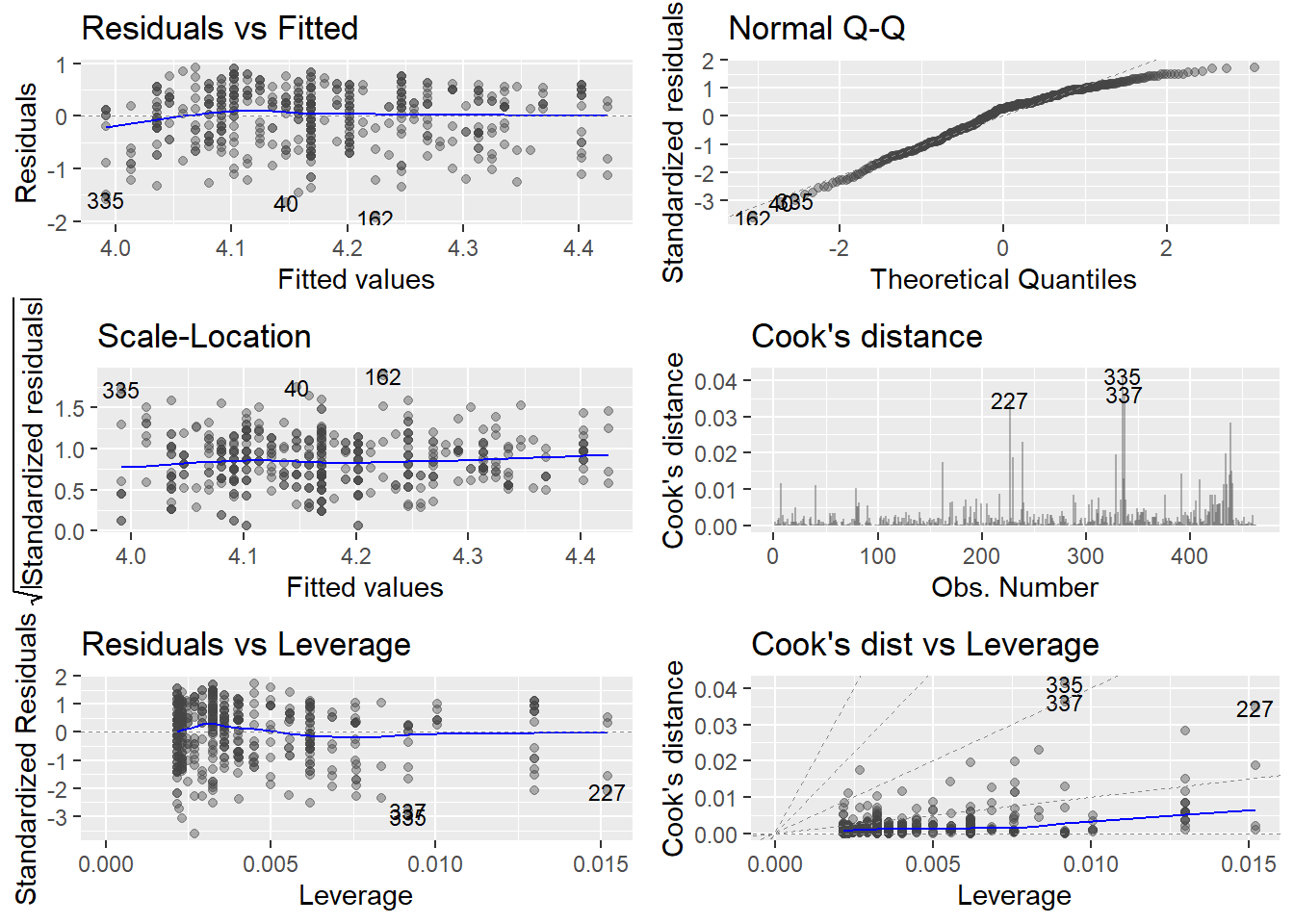 

Residuals vs Leverage(오른쪽 아래), Cook’s distance, Cook’s dist vs Leverage는 극단값 존재 여부를 나탄낸다.

10.1.2 극단값

극단값은 말 그대로 극단적인 개별 관측값이다. 극단적인만큼 분석할때 주의가 필요하다.

• 이상치(outlier)
  • 매우 큰 양수 혹은 매우 작은 음수의 잔차로서 회귀모형으로 잘 예측되지 않는 관측값
• 큰지레점(high leverage point)
  • 비정상적인 독립변수의 값에 의한 관측값. 독립변수 축에 있는 이상치에 해당한다. 종속변수의 값은 관측치의 영향력을 계산하는 데 사용하지 않는다.
• 영향관측치(influential observation)
  • 통계 모형 계수를 결정할 때 불균형하게 영향을 미치는 관측값이다. Cook’s distance로 확인할 수 있다.

autoplot()에서 Cook’s distance만 따로 표시해보자. 관측값 227, 337, 335가 극단값으로 나타났다. 극단값이 나타나면 극단값을 포함한 모형과 제거한 모형을 모두 확인해봐야 한다.

evals %>% 
  lm(score ~ bty_avg, .) %>% 
  autoplot(alpha = .4, label.size = 4, which = c(4, 6))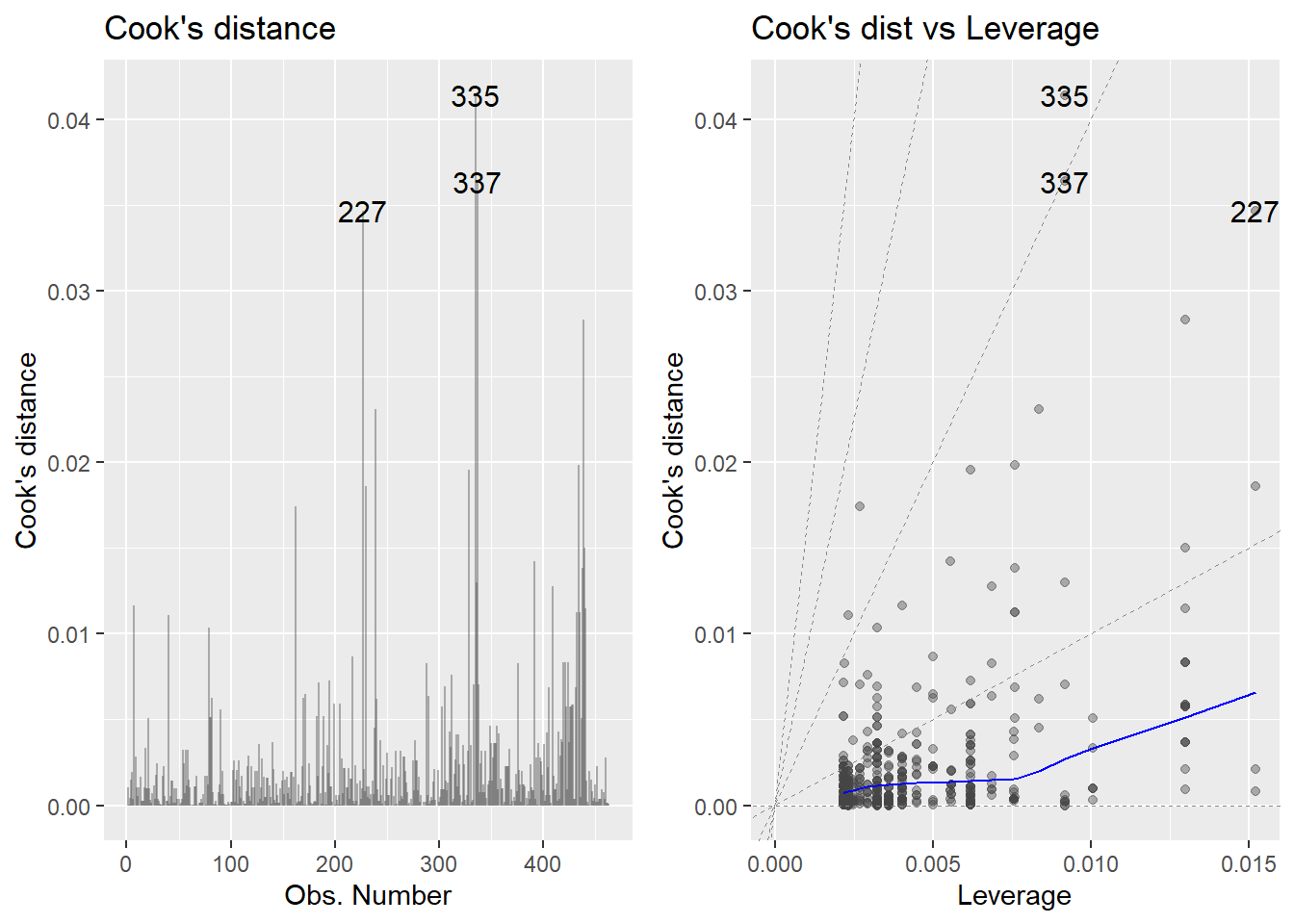 

10.1.3 다중공선성

다중공선성(multicolinearity)은 복수의 독립변수를 투입하는 다중회귀분석에서 발행할 수 있는 문제다.

• 공선성(collinearity): 하나의 독립변수와 다른 하나의 독립변수와 서로 상관성이 높은 경우.

• 다중공선성(multicollinearity) 하나의 독립변수와 다른 여러 독립변수와 서로 상관성이 높은 경우.

다중공선성 여부는 분산팽창요인(VIF: variance inflation factor)를 이용해 판단할 수 있다. 변수 사이의 상관성 때문에 분산이 팽창됐는지 나타낸다.

분산팽창요인은 car패키지의 vif()함수로 계산할 수 있다. 보통 4이상이면 다중공선성 문제가 있는 것으로 판단한다 (연구자에 따라서는 10을 판단기준으로 삼기도 한다).

regclass패키지의 데이터셋 SALARY을 이용해 다중공선성 문제를 살펴보자. 모든 변수의 분산팽창요인이 4 미만이므로 다중공선성 문제가 없다.

data(SALARY)
SALARY %>% lm(Salary ~ ., .) %>% vif()

##  Education Experience     Months     Gender 
##   1.134993   1.019070   1.016372   1.131650

regclass패키지의 데이터셋 BODYFAT으로 다중공선성 문제를 보자. 체지방(BodyFat)을 종속변수로 했을 때, 독립변수로 투입한 Weight Neck Chest Abdomen Hip Thigh Knee의 분산팽창요인이 4보다 크다.

data(BODYFAT)
BODYFAT %>% 
  lm(BodyFat ~ ., .) %>% vif()

##       Age    Weight    Height      Neck     Chest   Abdomen       Hip     Thigh 
##  2.250450 33.509320  1.674591  4.324463  9.460877 11.767073 14.796520  7.777865 
##      Knee     Ankle    Biceps   Forearm     Wrist 
##  4.612147  1.907961  3.619744  2.192492  3.377515

모든 변수를 독립변수로 투입한 다중회귀분석을 해보자. 모형 전체를 보면 \(F\) 통계량에 대한 유의확률이 0.001 이하로 통계적으로 유의하다. 그런데, 개별변수의 통계량을 보면 Weight Chest Hip Thigh Knee는 통계적으로 유의하지 않다.

BODYFAT %>% 
  lm(BodyFat ~ ., .) %>% summary()

## 
## Call:
## lm(formula = BodyFat ~ ., data = .)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -10.264  -2.572  -0.097   2.898   9.327 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -15.29255   16.06992  -0.952  0.34225    
## Age           0.05679    0.02996   1.895  0.05929 .  
## Weight       -0.08031    0.04958  -1.620  0.10660    
## Height       -0.06460    0.08893  -0.726  0.46830    
## Neck         -0.43754    0.21533  -2.032  0.04327 *  
## Chest        -0.02360    0.09184  -0.257  0.79740    
## Abdomen       0.88543    0.08008  11.057  < 2e-16 ***
## Hip          -0.19842    0.13516  -1.468  0.14341    
## Thigh         0.23190    0.13372   1.734  0.08418 .  
## Knee         -0.01168    0.22414  -0.052  0.95850    
## Ankle         0.16354    0.20514   0.797  0.42614    
## Biceps        0.15280    0.15851   0.964  0.33605    
## Forearm       0.43049    0.18445   2.334  0.02044 *  
## Wrist        -1.47654    0.49552  -2.980  0.00318 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.988 on 238 degrees of freedom
## Multiple R-squared:  0.749,  Adjusted R-squared:  0.7353 
## F-statistic: 54.63 on 13 and 238 DF,  p-value: < 2.2e-16

다중회귀분석에서 구하는 회귀계수는 다른 변수들이 일정할 때 한 독립변수가 종속변수에 영향을 미치는 정도다.

Weight Chest Hip Thigh Knee는 상당히 높은 상관관계를 이룬다.

BodyFat에 대해 Weight Chest Hip Thigh Knee을 동시에 투입해 다중회귀를 하는 것은 Weight가 일정할 때 Weight를 통제하고 회귀분석하는 것과 비슷한게 된다. Chest Hip Thigh Knee 등 다른 독립변수도 마찬가지다.

이는 분석 모형 계수들에 대한 신뢰구간이 부풀려져 각 독립변수의 회귀계수를 제대로 해석 할수 없게 된다.

변수들이 서로 독립적이지 않고 상호 상관성이 높은 다중 공선성이 나타나면 변수를 줄여 분석 모형을 재구성한다.

10.2 모형교정

회귀모형 진단 결과 문제가 나타나면 다음 방법을 시도해본다.

• 관측값 제거
• 변수의 변환
• 다른 분석방법 사용

10.2.1 관측값 제거

관측값 제거는 극단값이 관측됐을때 고려할 수 있다. 극단값을 제거한 모형의 결과와 제거하기 전 모형의 결과를 비교해, 극단값의 영향을 파악해야 한다. evals자료에서 극단값으로 나타난 관측값 227, 337, 335를 제거하기 전과 후의 결과를 비교해보자.

evals %>% 
  lm(score ~ bty_avg, .) %>% tidy() %>% 
  select.(term, p.value) %>% 
bind_cols.(
  evals %>% 
    filter.(!ID %in% c(227, 335, 337)) %>% 
    lm(score ~ bty_avg, .) %>% tidy() %>% 
    select.(p.value)
  ) %>% gt() %>% 
  tab_header("극단값 제거 전후 유의확률 비교") %>% 
  fmt_number(-1, decimals = 5)

## New names:
## * p.value -> p.value...2
## * p.value -> p.value...3

극단값 제거 전후 유의확률 비교
term	p.value...2	p.value...3
(Intercept)	0.00000	0.00000
bty_avg	0.00005	0.00013

극단값을 제거해도 유의수준 0.001수준에서 차이가 없으므로 극단값의 영향은 무시해도 된다.

만일, 극단값을 제거한 다음에 유의확률이 크게 바뀐다면 두 결과를 모두 보고하고 그 의미에 대하여 논의한다.

다음은 별의 표면온도와 밝기의 관계에 대한 자료다.

"https://raw.githubusercontent.com/dataminds/art/main/files/stars.csv" %>% 
  import() -> df
skim(df)

Table 10.1: Data summary

Name	df
Number of rows	47
Number of columns	2
_______________________
Column type frequency:
numeric	2
________________________
Group variables	None

Variable type: numeric

skim_variable	n_missing	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
temperature	0	1	4.31	0.29	3.48	4.28	4.42	4.46	4.62	▁▁▁▆▇
light	0	1	5.01	0.57	3.94	4.54	5.10	5.44	6.29	▅▅▇▅▂

• temperature: 별의 표면 온도
• light: 별의 밝기

df %>% 
  ggplot(aes(temperature, light)) +
  geom_point() +
  geom_smooth(method = lm, se = F) +
  labs(title = "별의 표면온도와 밝기의 관계")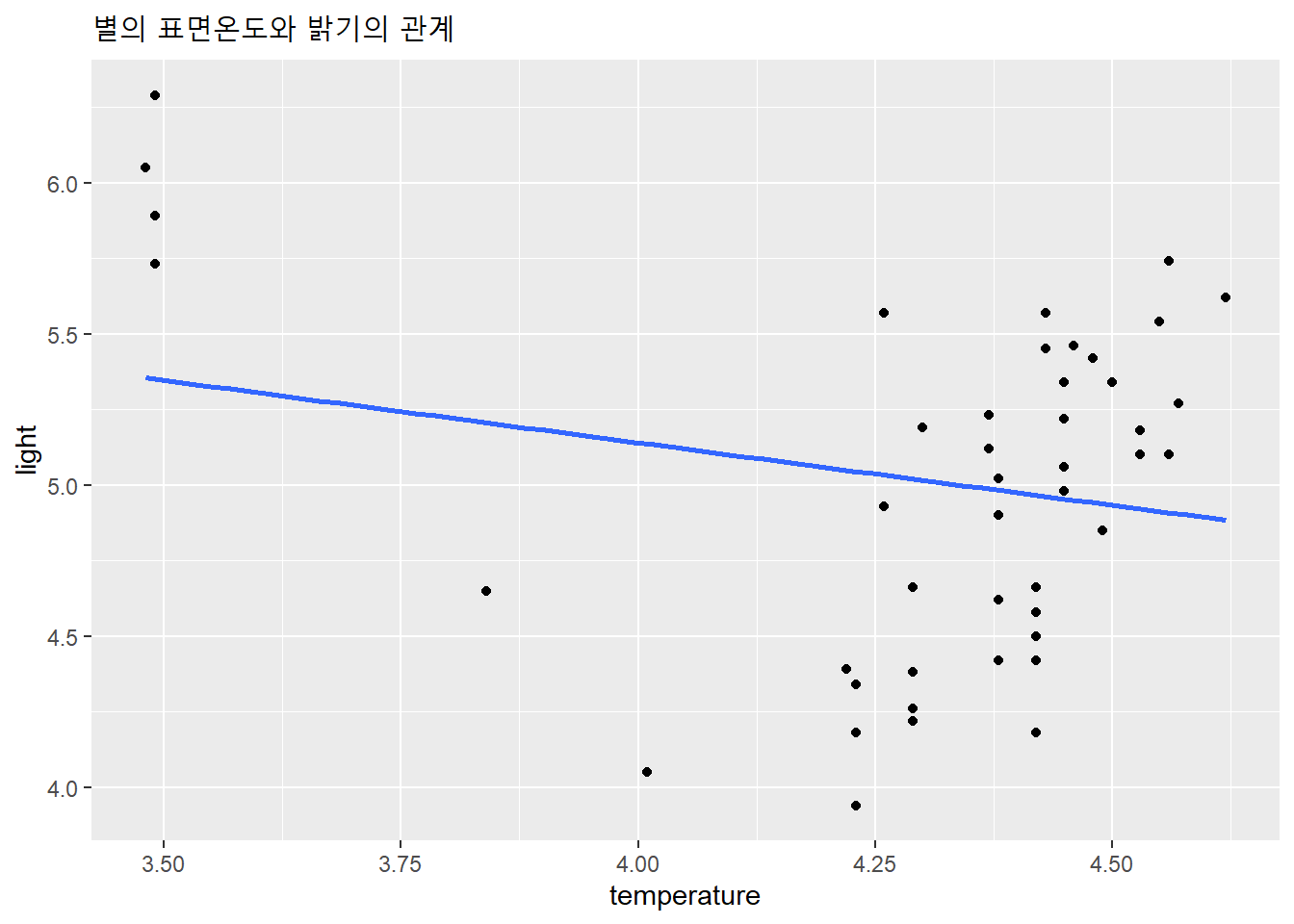

별의 표면온도와 밝기 사이에 나타난 선형관계는 표면온도가 매우 낮은 별 4개의 극단값 영향이 크다. 따라서 이 4개의 극단값을 포함한 결과와 제거한 결과를 모두 보고한다.

df %>% 
  lm(light ~ temperature, .) %>% tidy() %>% 
  select.(term, estimate, p.value) %>% 
bind_cols.(
  df %>% 
    filter.(temperature > 3.6) %>% 
    lm(light ~ temperature, .) %>% tidy() %>% 
    select.(estimate, p.value)
  ) %>% gt() %>% 
  tab_header("극단값 제거 전후 유의확률 비교") %>% 
  fmt_number(-1, decimals = 5)

## New names:
## * estimate -> estimate...2
## * p.value -> p.value...3
## * estimate -> estimate...4
## * p.value -> p.value...5

극단값 제거 전후 유의확률 비교
term	estimate...2	p.value...3	estimate...4	p.value...5
(Intercept)	6.79347	0.00000	−4.05652	0.03352
temperature	−0.41330	0.15572	2.04666	0.00002

df %>% 
  # 별표면 온도를 상하로 구분한 열 생성
  mutate.(t2 = ifelse(temperature < 3.6, "Low", "High")) %>% 
ggplot(aes(temperature, light)) +
  geom_point() +
  # 별표면 온도 상하로 구분 +
  geom_smooth(method = lm, se = F) +
  geom_smooth(aes(color = t2), method = lm, se = F) +
  labs(title = "별표면온도로 구분한 별의 밝기")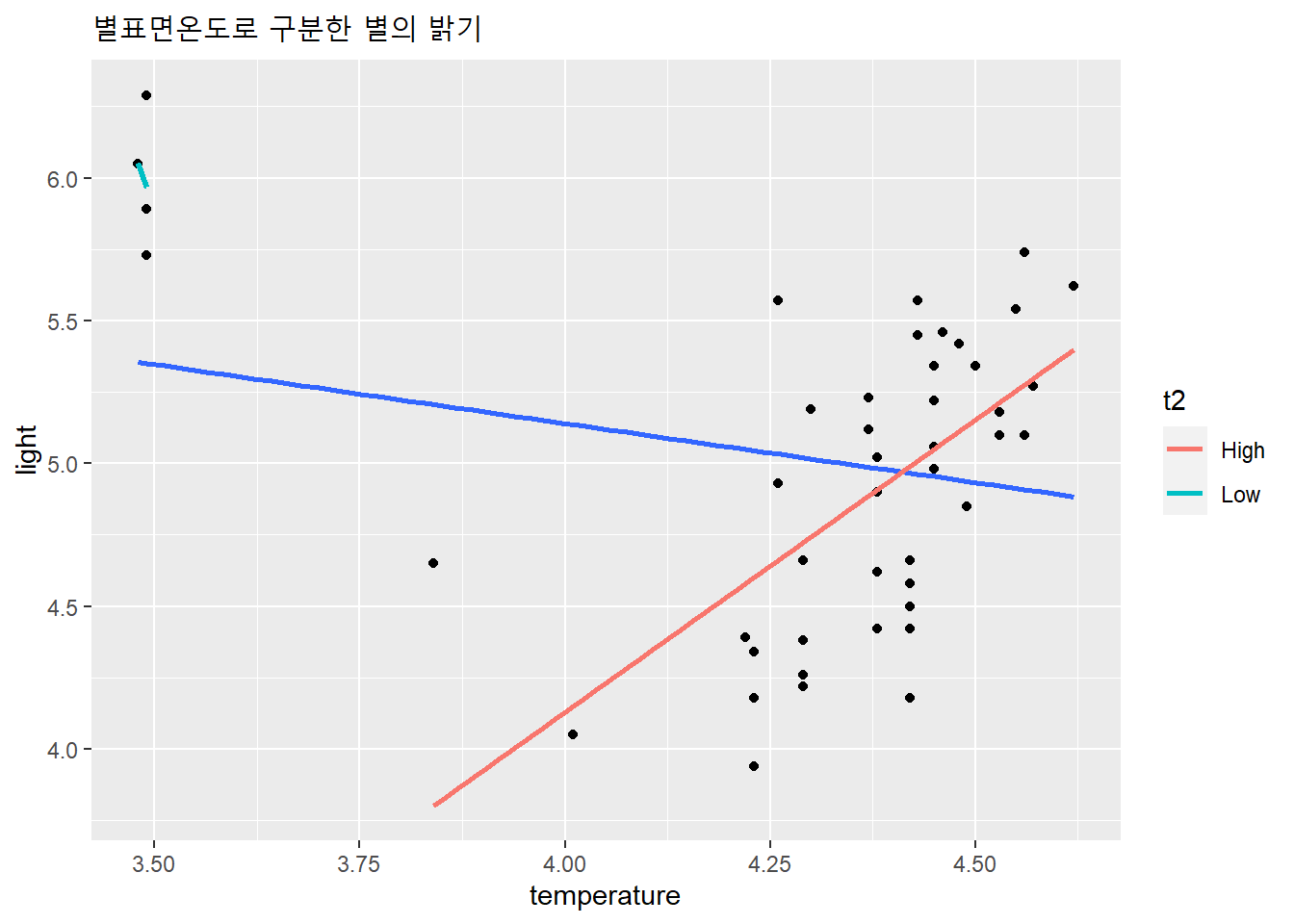

별의 표면온도와 별의 밝기는 통계적으로 유의한 관계가 나타나지 않지만, 표면온도가 극단적으로 낮은 별 4개를 제외하면 표면온도가 높을 수록 별의 밝아지는 관계가 통계적으로 유의하게 나타난다.

10.2.2 변수의 변환

선형회귀모형의 전제인 LINE에서 독립성을 제외한 선형성, 정규성, 등분산성의 가정을 충족하지 못하는 경우, 변수를 수학적으로 변환하면 전제 미충족 문제가 해결되는 경우가 있다.

변수의 변환은 변수 \(Y\)를 \(Y^\lambda\)로 교체한다.

lambda(\(\lambda\))	\(-2\)	\(-1\)	\(-0.5\)	\(0\)	\(0.5\)	\(1\)	\(2\)
변환	\(1/Y^2\)	\(1/Y\)	\(1/\sqrt{Y}\)	\(1/log(Y)\)	\(1/\sqrt{Y}\)	\(Y\)	\(Y^2\)

모형이 정규성의 전제를 충족하지 않는 경우 종속변수를 변환해 본다. car패키지의 powerTransform()함수가 변수 \(Y\)에 대하여 \(Y^\lambda\)로 정규화할 가능성이 높은 지수 \(\lambda\)를 찾아 준다.

powerTransform(evals$score) %>% summary

## bcPower Transformation to Normality 
##             Est Power Rounded Pwr Wald Lwr Bnd Wald Upr Bnd
## evals$score    3.0859        3.09       2.4126       3.7593
## 
## Likelihood ratio test that transformation parameter is equal to 0
##  (log transformation)
##                            LRT df       pval
## LR test, lambda = (0) 97.85665  1 < 2.22e-16
## 
## Likelihood ratio test that no transformation is needed
##                            LRT df      pval
## LR test, lambda = (1) 41.84487  1 9.881e-11

다만, 아래 사례처럼 수학적 변형이 반드시 정규성 문제를 해결하는 것은 아니다.

evals %>% 
  lm(score ~ bty_avg, .) %>% augment() %>% 
ggplot(aes(sample = .resid)) +
  geom_qq_line(color = 'cornflowerblue', size = 2) +
  geom_qq(alpha = .4) + 
  labs(title = "잔차의 QQ plot",
       subtitle = "lm(score ~ bty_avg)",
       x = "이론적 quantile",
       y = "잔차의 quantile") -> p1

evals %>% 
  mutate.(score2 = score^3.0859) %>% 
  lm(score2 ~ bty_avg, .) %>% augment() %>% 
ggplot(aes(sample = .resid)) +
  geom_qq_line(color = 'cornflowerblue', size = 2) +
  geom_qq(alpha = .4) + 
  labs(title = "잔차의 QQ plot",
       subtitle = "lm(score^3.0859 ~ bty_avg)",
       x = "이론적 quantile",
       y = "잔차의 quantile") -> p2

p1 + p2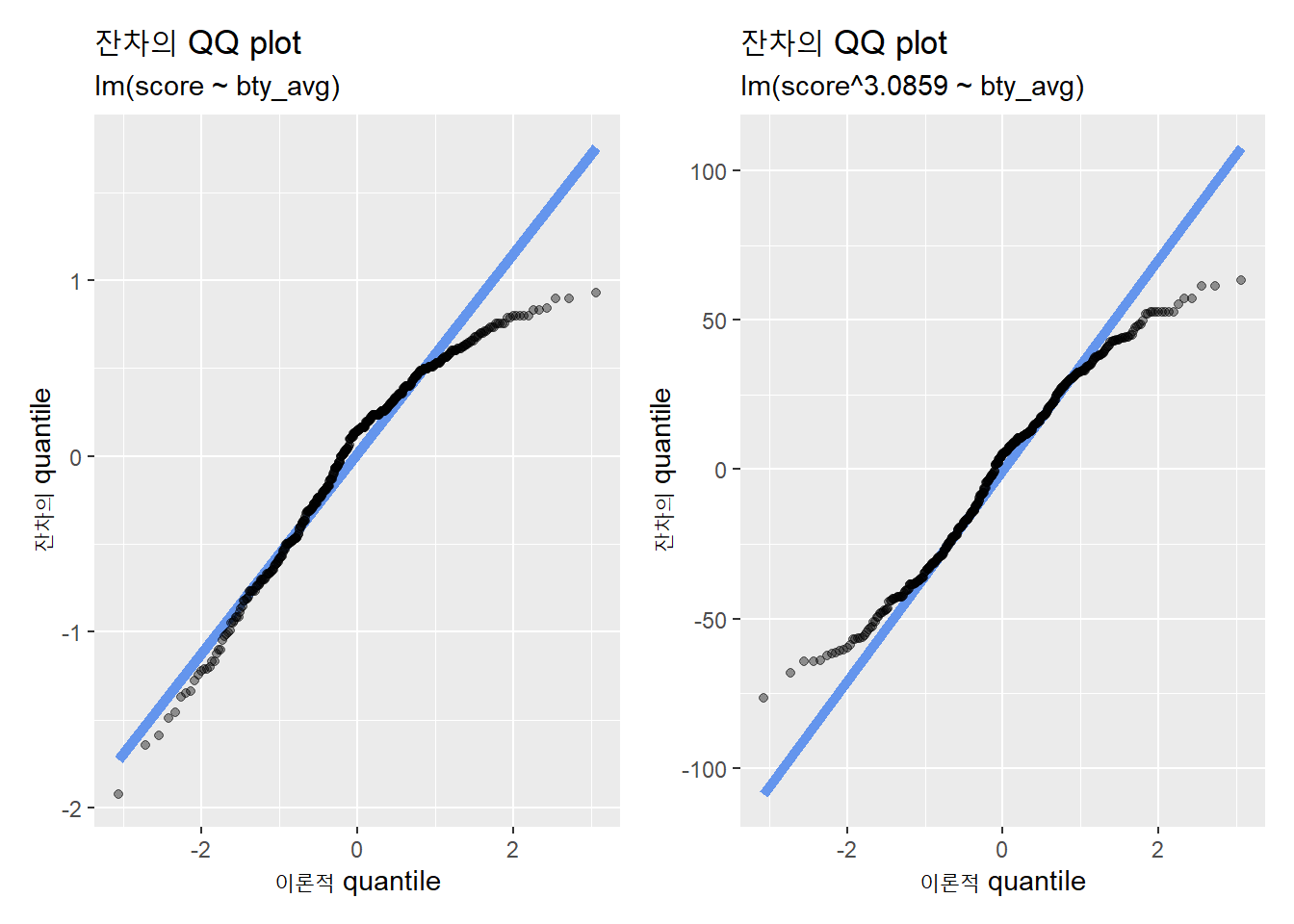

evals %>% 
  mutate.(score2 = score^3.0859) %>% 
  lm(score2 ~ bty_avg, .) %>% augment() %>% 
  pull.(.resid) %>% 
  shapiro.test()

## 
##  Shapiro-Wilk normality test
## 
## data:  .
## W = 0.97943, p-value = 3.945e-06

10.2.3 다른 분석방법 사용

선형회귀모형의 전제를 충족하지 않는다면, 변수를 변형하기 보다 선형회귀모형의 전제를 요구하지 않는 분석방법을 이용하는 것이 좋다.

R에는 비선형, 비모수 등 다양한 회귀모형을 분석할 수 있는 함수가 제공된다. Vito Ricci는 200여개의 함수를 정리해 놓기도 했다.

10.2.3.1 회귀모형의 종류

회귀분석의 유형	분석 용도
단순 선형(simple linear)	단일 독립변수와 단일 연속형 종속변수
다중 선형(multiple linear)	2개 이상의 독립변수
능형(ridge)	독립변수의 다중공선성 문제
다항(polynomial)	n차 다항의 독립변수(예: \(Y = a + b_1X^2 + b_2X + e\))
시계열(time-series)	반복측정된 독립변수
다수준(multilevel)	반복측정된 독립변수 혹은 집단 및 개인 수준의 변수가 혼재
다변량(multivariate)	2개 이상의 종속변수
로지스틱(logistic)	범주형 종속변수(예: 성공/실패)
포아송(poisson)	비율 종속변수(예: 발생률)
음이항(negative binomial)	분산이 큰 종속변수
견고(robust)	극단값 포함 변수
비선형(nonlinear)	선형이 아닌 모형
비모수(nonparametric)	정규분포가 아닌 변수

단순선형회귀모형의 적합을 개선하기 위한 대안의 회귀모형을 선택하는 결정은 복잡하기 때문에 별도의 고급통계를 통해 학습한다. 여기서는 비모수 통계로서 많이 활용되는 시뮬레이션 기반 회귀분석 사례만 다룬다.

10.2.3.2 시뮬레이션기반 회귀분석

evals데이터셋으로 단순선형모형으로 적합값을 구한 다음, 앞서 학습한 시뮬레이션기반 회귀모형으로 적합값을 구해 비교해 보자.

evals %>% lm(score ~ bty_avg, .) %>% tidy() %>% 
  gt() %>% 
  tab_header("이론기반 회귀분석의 유의확률") %>% 
  fmt_number(-1, decimals = 2) %>% 
  fmt_number(p.value, decimals = 3)

이론기반 회귀분석의 유의확률
term	estimate	std.error	statistic	p.value
(Intercept)	3.88	0.08	50.96	0.000
bty_avg	0.07	0.02	4.09	0.000

재표집 5000번 부트스래핑해 기울기의 신뢰구간을 구해보자.

# 기울기의 점 추정치
obs_slope <-
evals %>% 
  specify(score ~ bty_avg) %>% 
  calculate(stat = 'slope')
obs_slope

## Response: score (numeric)
## Explanatory: bty_avg (numeric)
## # A tibble: 1 x 1
##     stat
##    <dbl>
## 1 0.0666

# 부스트래핑 
boot_slope <-
evals %>% 
  specify(score ~ bty_avg) %>% 
  generate(reps = 5000, type = 'bootstrap') %>% 
  calculate(stat = 'slope') 
boot_slope %>% head()

## Response: score (numeric)
## Explanatory: bty_avg (numeric)
## # A tibble: 6 x 2
##   replicate   stat
##       <int>  <dbl>
## 1         1 0.0560
## 2         2 0.0642
## 3         3 0.0639
## 4         4 0.0752
## 5         5 0.0658
## 6         6 0.0532

# 표준오차 기반 신뢰구간 계산
boot_slope %>% 
  get_ci(type = 'se', point_estimate = obs_slope, level = .95)

## # A tibble: 1 x 2
##   lower_ci upper_ci
##      <dbl>    <dbl>
## 1   0.0326    0.101

95% 신뢰수준으로 구한 구간이 기울기 0을 포함하지 않는다.

유의확률도 유의수준0.05에서 통계적으로 유의하다. 앞서 이론 기반으로 추론한 유의한 결과와 일치한다.

perm_slope <- 
evals %>% 
  specify(score ~ bty_avg) %>% 
  hypothesize(null = 'independence') %>% 
  generate(reps = 5000, type = 'permute') %>% 
  calculate(stat = 'slope')

perm_slope %>% 
  get_p_value(obs_stat = obs_slope, direction = 'both')

## # A tibble: 1 x 1
##   p_value
##     <dbl>
## 1       0

10.3 모형선택

회귀모형의 구성은 선택의 과정이다. 가능한 모형이 다양하기 때문이다. 모든 변수를 포함하거나 중요하지 않은 변수는 제거할 수 있고, 다항회귀나 상호작용항을 투입할 수도 있다.

모형의 선택은 분석 목적에 따라 달라진다. 회귀분석의 목적은 크게 추론과 예측으로 구분할 수 있다.

추론(inference)은 독립변수에 초점을 둔 접근이다. 어떤 현상이 있을 때, 그 현상의 원인을 추론하는 것이 목적이다. 독립변수에 대한 의사결정을 할때, 즉, 독립변수에 대해 개입하거나 조작함으로써 기대하는 결과를 얻고자 할때 유용하다.

예를 들어, 전염병 창궐 상황에서 새로 개발된 백신접종을 해야 하는지 말아야 하는지, 혹은 신제품을 출시했을 때 어떤 내용의 메시지를 활용해야 하는지 등의 상황에 적용할 수 있다.

추론에는 인과효과 추정(estimation of effects of causes)과 원인의 추적(investitation of causes of effect)으로 구분 가능하다.

• 인과효과 추정: 이미 주어진 원인의 효과를 추정
  • 예: 다른 요인들을 모두 통제했을 때 성이 원인으로 작용해 급여수준을 결정하는지 추정
• 원인의 추적: 가장 중요한 영향을 미친 변수 추적
  • 예: 경험, 교육수준, 근무기간, 성 등 4개 변수 중 급여수준에 가장 중요한 영향은 미치는 변수 추적

예측(prediction)은 종속변수에 초점을 둔 접근이다. 어떤 현상이 있을 때, 그 현상과 관련된 다른 현상 혹은 그 현상으로 인해 발생할수 있는 종속변수를 파악하는 것이 목적이다. 독립변수에 개입하거나 조작하는게 아니라, 여러 발생가능한 결과 중 활용가능한 최적의 산출물에 관련된 종속변수를 도출하는 것이 목적이다.

예를 들어, 사람들이 어떤 행동(예: 투표)을 할지 예측할 수 있는 지표(예: 페이스북의 친구연결망과 좋아요를 클릭하는 글의 종류)를 찾아내는 상황에 적용할 수 있다.

예측은 연관성만을 고려하기 때문에 관련된 두 변수가 반드시 인과관계를 의미하지는 않는다. 비록 인과관계가 아니어도 연관성이 있다는 현상을 찾아낸다는 것은 현실적으로 매우 중요한 의미를 지니게 된다.

예를 들어, 특정한 조건(나이, 혈압, 병력 등)이 사람들이 뇌졸중 여부를 예측할 수 있는 변수로 확인된다면, 이를 지표를 이용해 뇌졸중 취약집단을 추려낼 수 있고, 이들 집단에 대해 독립변수(예: 스타틴)를 투입해 뇌졸중 가능성을 줄일 수 있는 조치를 취할 수 있기 때문이다.

분석목적에 따라 모형을 어떻게 선택해야 하는지 살펴보자.

10.3.1 모든 부분집합 회귀(All Subset Regression)

다중회귀모형에서 일반적으로 사용하는 모형선택은 AIC(Akaike’s An Information Criterion) 지표를 이용해 변수를 추가하거나 제거하는 방법이다. R에서는 step()함수를 이용해 계산할 수 있다.

• Backward regression: 먼저 가능한 많은 변수를 포함하는 모형을 만든 다음 변수를 하나씩 제거

• Forward regression: 먼저 가장 적은 수의 변수로 모형을 만든 다음, 변수를 하나씩 추가.

• Stepwise regression: 단계적으로 변수를 빼거나 더하며 모형을 구성.

단계적으로 변수를 빼거나 더하는 방법은 그리 좋은 방법은 아니다. 가능한 모든 모형을 비교하지 않기 때문이다.

leaps패키지의 resubsets()함수를 이용하면 모든 경우(all subset)의 모형을 비교해 ’최선’의 모형을 찾을 수 있다. SALARY데이터셋의 경우, 독립변수가 4개 이므로 nbest =인자에서 독립변수의 수만큼 지정하면 가능한 모든 경우의 모형을 만들어 비교한다.

data(SALARY)
names(SALARY)

## [1] "Salary"     "Education"  "Experience" "Months"     "Gender"

regsubsets(Salary ~ ., data = SALARY, nbest = 4) %>% 
  summary()

## Subset selection object
## Call: regsubsets.formula(Salary ~ ., data = SALARY, nbest = 4)
## 4 Variables  (and intercept)
##            Forced in Forced out
## Education      FALSE      FALSE
## Experience     FALSE      FALSE
## Months         FALSE      FALSE
## GenderMale     FALSE      FALSE
## 4 subsets of each size up to 4
## Selection Algorithm: exhaustive
##          Education Experience Months GenderMale
## 1  ( 1 ) " "       " "        " "    "*"       
## 1  ( 2 ) "*"       " "        " "    " "       
## 1  ( 3 ) " "       " "        "*"    " "       
## 1  ( 4 ) " "       "*"        " "    " "       
## 2  ( 1 ) " "       " "        "*"    "*"       
## 2  ( 2 ) "*"       " "        " "    "*"       
## 2  ( 3 ) " "       "*"        " "    "*"       
## 2  ( 4 ) "*"       " "        "*"    " "       
## 3  ( 1 ) "*"       " "        "*"    "*"       
## 3  ( 2 ) " "       "*"        "*"    "*"       
## 3  ( 3 ) "*"       "*"        " "    "*"       
## 3  ( 4 ) "*"       "*"        "*"    " "       
## 4  ( 1 ) "*"       "*"        "*"    "*"

변수 하나로만 만든 모형 4개, 변수 두개로 만든 모형 4개, 변수 세개로 만든 모형 4개, 변수 네개를 모두 투입한 모형 1개 등 가능한 모든 모형을 만들었다.

각 모형의 성능은 수정결정계수 \(adj R^2\)로 정렬한 도표를 plot()함수로 산출해 비교할 수 있다.

regsubsets(Salary ~ ., data = SALARY, nbest = 4) %>% 
  plot(scale = 'adjr2')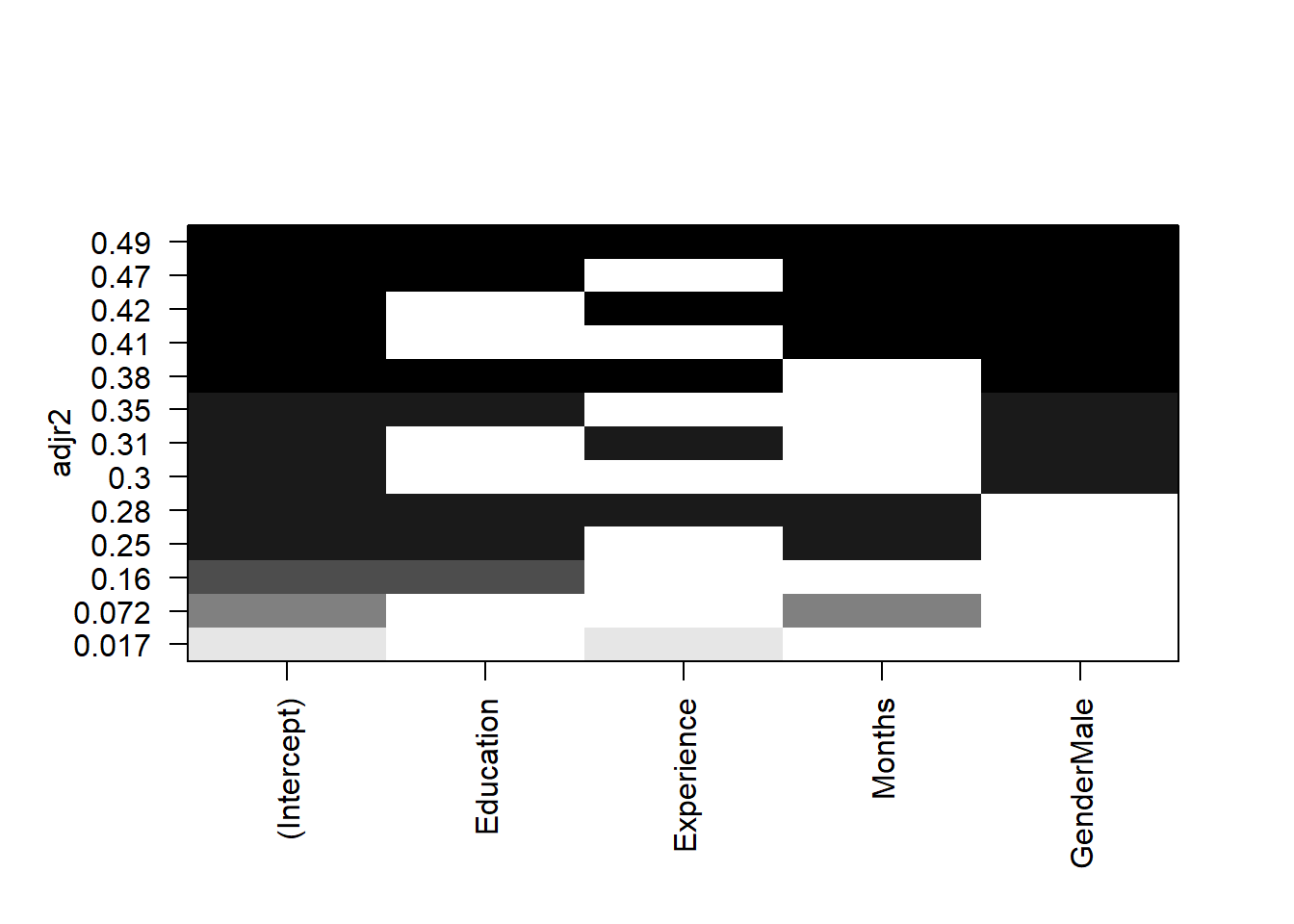

X축이 독립변수이고 Y축이 수정결정계수다. 검정으로 표시된 부분이 X축 독립변수가 투입된 것을 나타낸다.

Y축 가장 위 수정결정계수 0.49를 모면, 독립변수 4개가 모두 검정색으로 표시돼 있다. 독립변수 4개를 모두 투입한 모형의 설명력이 가장 높다는 것을 보여준다. 흥미로운 현상은 급여를 예측하는 변수로 교육, 경력, 기간 등 3개 독립변수를 투입한 모형보다 성(Gender)을 단독으로 투입한 모형의 설명력이 더 높은 부분이다.

독립변수를 성만 투입만 모형, 성을 제외한 모든 변수를 투입한 모형(교육, 경력, 기간), 그리고 모든 변수를 투입한 모형 등 3개 모형을 AIC(Akaike’s An Information Criterion)값으로 비교해보자. AIC값이 적을 수수록 모형성능이 좋다.

SALARY -> df
df %>% lm(Salary ~ Gender, .) -> fit1
df %>% lm(Salary ~ Education + Experience + Months, .) -> fit2
df %>% lm(Salary ~ ., .) -> fit3
AIC(fit1, fit2, fit3)

##      df      AIC
## fit1  3 1380.935
## fit2  5 1385.111
## fit3  6 1354.027

변수 4개를 모두 투입한 모형의 AIC값이 가장 작다. 성만 투입한 모형의 AIC값이 성을 제외한 나머지 변수를 모두 투입한 모형보다 작다.

10.3.2 상대적 중요성

여러 독립변수 중 종속변수를 설명하는데 가장 중요한 변수가 무엇인지 에 대해서는 각 변수의 상대적 중요도에 따라 순위를 매길 수 있다. 각 변수의 상대적 중요도를 판단하는 간단한 방법은 각 변수에 scale()함수를 이용해 표준화한 다음 회귀분석을 해 비교하는 것이다.

• scale()함수에는 숫자형을 투입해야 하므로, Gender변수의 값을 숫자형으로 변경.
• scale()함수는 행렬로 산출하므로 as.data.frame()으로 데이터프레임으로 변환해 lm()함수에 투입한다.

df %>% 
  mutate.(Gender = ifelse(Gender == "Female", 1, 0)) %>% 
  scale() %>% as.data.frame() %>% 
  lm(Salary ~ ., .) %>% tidy() %>% 
  gt() %>% 
  tab_header("표준화 회귀계수를 이용한 독립변수의 상대적 중요성 비교") %>% 
  fmt_number(-1, decimals = 2)

표준화 회귀계수를 이용한 독립변수의 상대적 중요성 비교
term	estimate	std.error	statistic	p.value
(Intercept)	0.00	0.07	0.00	1.00
Education	0.29	0.08	3.65	0.00
Experience	0.16	0.08	2.16	0.03
Months	0.34	0.08	4.50	0.00
Gender	−0.49	0.08	−6.13	0.00

Gender의 회귀계수의 절대값이 다른 변수의 회귀계수에 비해 가장 크다. 즉, Gender가 한 단위 증가할때의 Salary의 변화가 다른 변수의 한단위 증가할 때의 Salary 변화보다 크다.

결정계수 \(R^2\)의 증가를 기준으로 상대가중치(Relative weights)를 이용하는 방법도 있다. 모든 가능한 하위 모형에서 독립변수를 추가했을 때 평균적인 \(R^2\)의 증가를 계산한다.

계산 방법은 다음과 같다. 이 코드는 Dr. Johnson의 논문에 있는 SPSS 프로그램을 R로 바꾼 것으로 에 인용된 것을 다시 인용한 것이다.

relweights <- function(fit,...){
         R <- cor(fit$model)
         nvar <- ncol(R)
         rxx <- R[2:nvar, 2:nvar]
         rxy <- R[2:nvar, 1]
         svd <- eigen(rxx)
         evec <- svd$vectors
         ev <- svd$values
         delta <- diag(sqrt(ev))
         lambda <- evec %*% delta %*% t(evec)
         lambdasq <- lambda ^ 2
         beta <- solve(lambda) %*% rxy
         rsquare <- colSums(beta ^ 2)
         rawwgt <- lambdasq %*% beta ^ 2
         import <- (rawwgt / rsquare) * 100
         import <- as.data.frame(import)
         row.names(import) <- names(fit$model[2:nvar])
         names(import) <- "Weights"
         import <- import[order(import),1, drop=FALSE]
         dotchart(import$Weights, labels=row.names(import),
            xlab="% of R-Square", pch=19, 
            main="Relative Importance of Predictor Variables",
            sub=paste("Total R-Square=", round(rsquare, digits=3)),
            ...)
         return(import)
}

모든 값이 숫자형이어야 하기 때문에 범주형인 Gender의 값을 숫자형으로 바꿨다.

df %>% mutate.(Gender = ifelse(Gender == "Female", 1, 0)) %>% 
  lm(Salary ~ ., .) %>% 
  relweights(col = 'deeppink')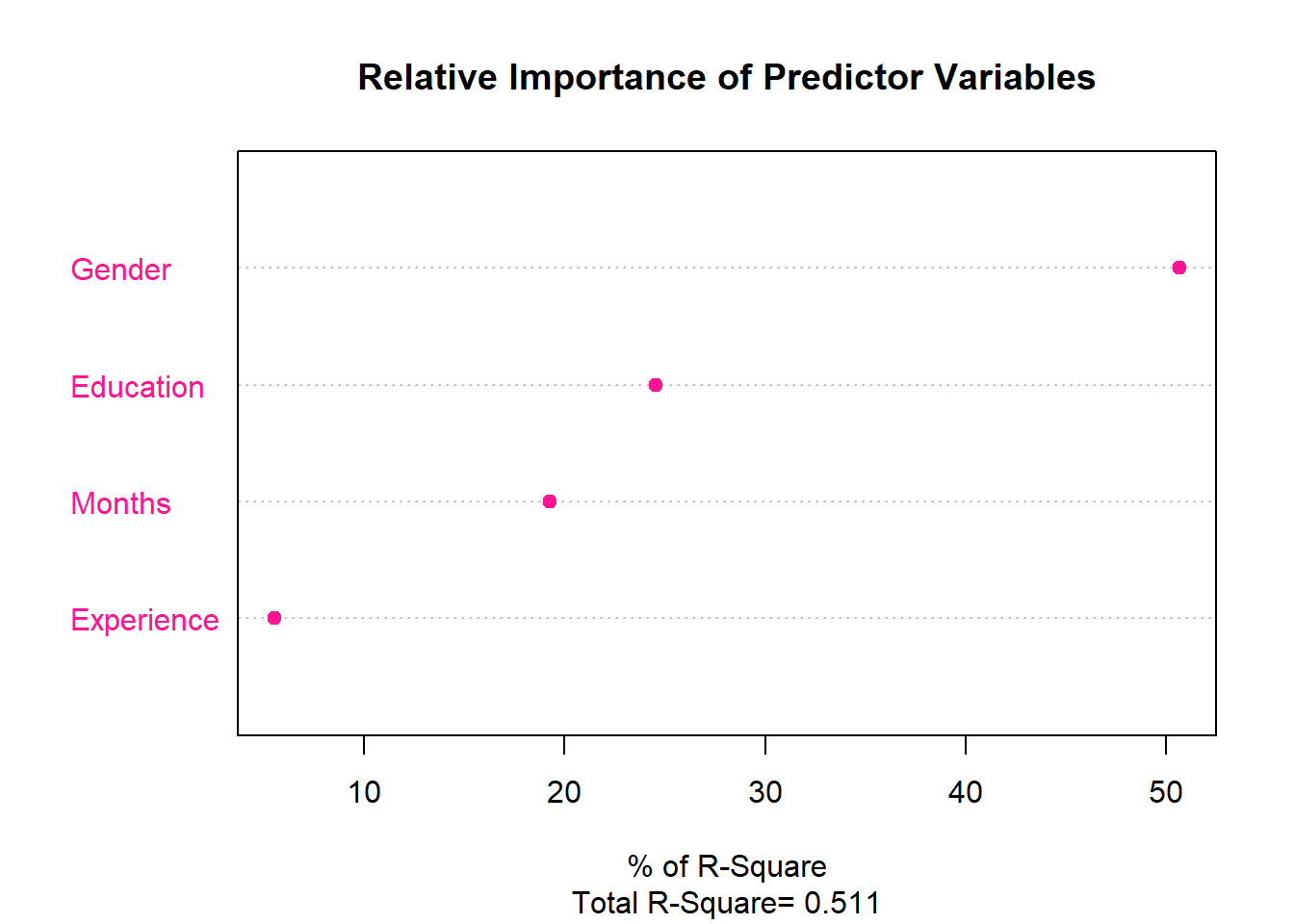

##              Weights
## Experience  5.502939
## Months     19.273926
## Education  24.525209
## Gender     50.697925

Gender의 설명력이 가장 크고, Education, Months, Experience의 순서로 설명력이 크다.

모형 설명력의 차이를 비교할 수 있는 anova()함수를 이용하면, 설명력이 가장 작은 Experience를 모형에 추가하는 것이 모형 설명력의 증가를 유의하게 향상시키는지 확인할 수 있다.

df %>% lm(Salary ~ Gender + Education + Months, .) -> fit1
df %>% lm(Salary ~ ., .) -> fit2
anova(fit1, fit2)

## Analysis of Variance Table
## 
## Model 1: Salary ~ Gender + Education + Months
## Model 2: Salary ~ Education + Experience + Months + Gender
##   Res.Df      RSS Df Sum of Sq      F  Pr(>F)  
## 1     89 10603660                              
## 2     88 10070523  1    533137 4.6587 0.03362 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

두 모형을 비교한 \(F\)검정에서 유의확률이 유의하므로 모형에 Experience변수를 추가하는 것이 모형의 설명력을 유의하게 향상시킨다고 판단할 수 있다.

다만, 0.05수준에서 유의확률이 0.034로서 유의하다고 판단할 수 있지만, 다른 방법(예: 교차검증)을 이용하면 유의하지 않을 수 있음에 주의한다. 다음 장 외적타당성에서 보다 자세하게 다룬다.

10.4 외적타당성

타당성(validity)는 명목적으로 나타낸 것이 실제로 적용된 정도이다.

예를 들어, 김포행 항공편이 김포공항으로 간다면 이는 타당성이 있는 항공편이다. 반면, 김포행이 인천공항에 도착한다면 타당성이 결여된 항공편이다.

외적타당성(external validity)은 표본을 통해 추론한 결과를 다른 표본(즉, 외부의 표본)에 대해서도 확장해 타당성을 확보할 수 있는 정도다.

내적타당성(internal validity)은 추론한 원인과 결과의 관계가 실제적인 원인과 결과의 관계를 반영하는 정도다. 독립변수의 설명한 종속변수가 실제로 해당 모형에 투입한 독립변수의 예측에 해당하는지, 혹은 종속변수의 설명요인으로 추론한 독립변수가 실제로 해당 모형에 투입한 종속변수의 설명요인에 해당하는지를 나타내는 정도다.

• 신뢰성(reliability)는 일관된 결과를 산출하는 정도. 예를 들어, 김포행 항공편이 매번 인천공항으로 간다면 이는, 타당성은 결여됐지만, 일관된 결과를 산출하므로 신뢰성이 확보된 항공편에 해당한다.

10.4.1 외삽의 오류

외삽(extrapolation)은 모형에 사용한 자료의 범위를 벗어난 영역에 대해 분석결과를 확장해 적용하는 것이다. 외삽은 관측된 자료를 토대로 추론하기에 일정부분 유의미하지만, 오류가능성도 높다. 주어진 자료에 최적화한 분석결과를 다른 자료에 적용할 때는 제대로 작동하지 않을 가능성도 있다.

독립변수와 종속변수의 관계가 모든 구간에서 늘 선형의 관계를 이룬다는 보장이 없기 때문이다.

예를 들어, 연령을 독립변수, 배우자의 수를 종속변수로 투입해 회귀모형을 구성한다고 하자. 20대에서는 배우자가 0명이고, 30대에는 배우자가 1명인 자료를 통해 선형회귀모형을 구성해, 40대에 외삽하면 배우자의 수는 2명이 되고, 50대에 외삽하면 3명이 된다.

10.4.2 과대적합 vs 과소적합

과대적합(overfitting)은 관측 자료에 과다하게 적합하여 생기는 문제다. 연구자가 수집한 표본에 대해서는 가장 정확한 적합값을 산출하지만, 그 표본의 결과를 다른 표본에 적용할 때 타당도가 떨어지는 문제가 생긴다. 반대로 과소적합(underfitting)은 관측자료에 과소하게 적합하여 생기는 문제다. 과도하게 단순화하여 예측 정확도가 떨어지는 문제가 있다.

일차함수보다 더 복잡한 고차함수나 국소가중치 혹은 평활스플라인 등을 이용하면 선형모형 보다 두 변수 사이의 관계를 더 정밀하게 묘사한 선을 구할 수 있다.

SALARY -> df
x <- 1:10
y <- c(0, -1, 2, 3, 5, 3, 1, -1, 1, 8)
ols_v <- lm(y ~ x) %>% predict()
poly_v <- lm(y ~ poly(x, 3))  %>% predict()
loess_v <- loess(y ~ x) %>% predict()
spline_v <- smooth.spline(x, y) %>% predict() %>% .$y

tidytable(
  x = x,
  y = y,
  ols = ols_v,
  poly = poly_v,
  loess = loess_v,
  spline = spline_v
) -> tb
tb %>% ggplot() +
  # https://colorbrewer2.org/#type=qualitative&scheme=Dark2&n=4
  geom_line(aes(x, ols), color = '#1b9e77', size = 1.4) +
  geom_line(aes(x, poly), color = '#d95f02', size = 1.4) +
  geom_line(aes(x, loess), color = '#7570b3', size = 1.4) +
  geom_line(aes(x, spline), color = '#e7298a', size = 1.4) +
  geom_point(aes(x, y), color = '#525252', size = 4) +
  annotate('text', x = 10.6, y = tb$ols[10], label = "OLS") +
  annotate('text', x = 11, y = tb$poly[10]-.2, label = "Polynomial") +
  annotate('text', x = 10.8, y = tb$loess[10]-.2, label = "LOESS") +
  annotate('text', x = 10.9, y = tb$spline[10], label = "SPLINE") +
  labs(title = "선형회귀선과 최적화 회귀선") +
  xlim(0, 11.5)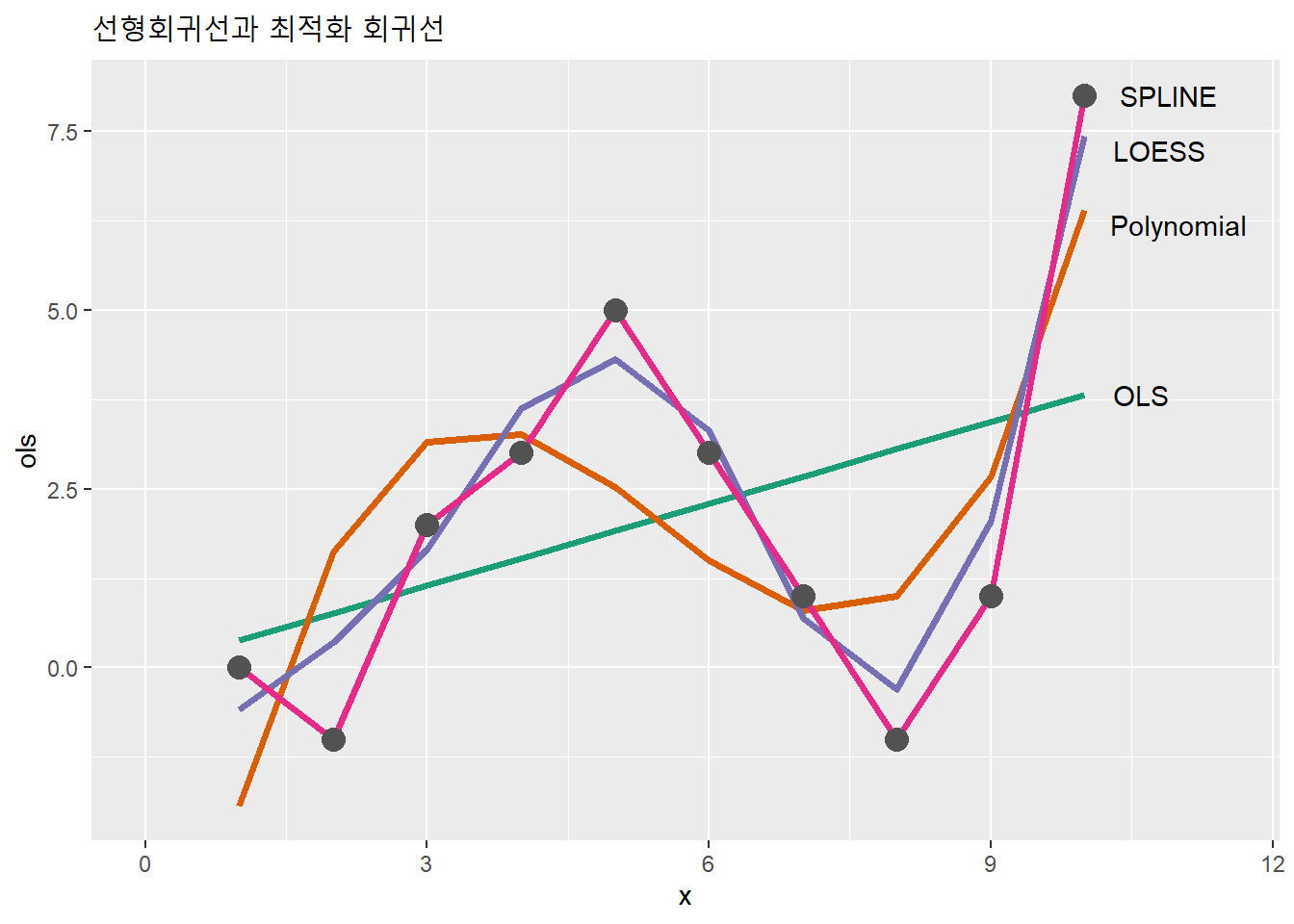

스플라인으로 구성한 회귀선이 자료에 가장 적합하고, 선형(OLS)으로 구성한 회귀선이 자료에 덜 적합한 것으로 보인다. 어림하여 볼때, 스플라인으로 구성한 회귀모형은 과대적합이고, 선형으로 구성한 회귀모형은 과소적합이라고 판단할 수 있다.

그렇다면, 단순한 선형회귀모형은 다른 최적화 방법에 비해 열등한 분석방법이라고 할 수 있을까? 맥락에 따라 다르다.

전반적인 관계를 파악하기 위해서라면 단순선형모형에 장점이 있고, 정밀한 관계 파악이 목적이라면 최적화 모형에 장점이 있다. 표본에 최적화한 모형은 다른 표본에 대해서는 확장성이 떨어지는 단점이 있다.

10.4.3 교차검증(cross-validation)

분석 모형의 외적 타당성 가능성을 확인하기 위해 교차검증(cross-validation)을 할수 있다. 교차검증은 표본의 일부를 훈련용으로 사용하고, 나머지를 확인용으로 사용해 모형의 외적 타당도를 검증하는 방법이다. 검증절차는 다음과 같다.

1. 표본을 나눠 훈련용 자료와 확인용 자료로 구분
2. 훈련용 자료로 회귀모형을 구성
3. 구성한 회귀모형을 확인용 자료에 적용

훈련자료와 확인자료는 서로 다른 데이터셋이기 때문에, 훈련자료로 구성한 회귀모형이 확인자료에도 잘 적용되면 그 회귀모형은 외적 타당성이 있다고 판단할 수 있다.

표본은 여러 방식으로 나눌 수 있지만, 이상적인 방법은 반복 K겹(K-fold)으로 나누는 방식이다. 즉, 표본을 k개의 하위표본으로 나눈 다음, 그중 하나를 확인자료로 이용하고, 나머지를 훈련자료로 이용하기를 반복하는 것이다. 예를 들어, 표본을 4개의 하위표본 s1, s2, s3, s4로 나눴다면 다음과 같이 훈련자료와 확인자료로 구분할 수 있다.

• 1차검증: s1, s2, s3로 훈련모형 구성하고, s4로 그 모형 확인
• 2차검증: s2, s3, s4로 훈련모형 구성하고, s1로 그 모형 확인
• 3차검증: s3, s4, s1로 훈련모형 구성하고, s2로 그 모형 확인
• 4차검증: s4, s1, s2로 훈련모형 구성하고, s3로 그 모형 확인

이렇게 반복하여 K겹 교차검증을 하면, 모든 표본에 대해 훈련과 확인을 해볼 수 있다.

반복교차검증은 caret패키지로 할수 있다.SALARY데이터셋을 5겹 반복 교차검증을 해보자. 반복교차검증 순서는 다음과 같다.

1. k겹 교차 하위표본 구성: trainControl(method = 'repeatedcv')
2. 모형 훈련: train()
3. 재표집하며 모형평가: resamples()

trainConrol()함수에서 method =인자를 이용해 다양한 교차검증 방법을 지정할 수 있다. 기본값은 boot. 자세한 내용은 설명문서 참조.

data(SALARY)
SALARY -> df
names(df)

## [1] "Salary"     "Education"  "Experience" "Months"     "Gender"

set.seed(37)
# 5겹 교차 하위표본 구성
train_control <- 
  trainControl(method = 'repeatedcv',  # 반복교차 지정
               number = 5, repeats = 5) # k겹 개수 지정
# 모형훈련
model1 <- df %>% train(
  # 모형과 데이터셋
  Salary ~ Gender, data = ., 
  # 분석방법 
  method = 'lm', 
  # 훈련자료
  trControl = train_control)
model2 <- df %>% train(
  Salary ~ Education + Months + Gender, data = .,
  method = 'lm', trControl = train_control)
model3 <- df %>% train(
  Salary ~ Education + Months + Gender + Experience, data = .,
  method = 'lm', trControl = train_control)
# 재표집하며 모형평가. 기본값은 25회 
list(model1, model2, model3) %>% resamples() -> resamp_l

각 모형의 성능을 평가하는 지표는 다음과 같다.

• 평균절대오차(MAE: Mean Absolute Error).
  • 작을수록 모형성능이 좋다.
• 평균제곱근오차(RMSE: Root Mean Square Error)
  • 작을수록 모형성능이 좋다.
• 피어슨 상관계수 제곱(\(R^2\))
  • 클수록 모형성능이 좋다.

25개의 표본에 대한 분석 결과는 summary()함수로 요약할 수 있다.

resamp_l %>% summary()

## 
## Call:
## summary.resamples(object = .)
## 
## Models: Model1, Model2, Model3 
## Number of resamples: 25 
## 
## MAE 
##            Min.  1st Qu.   Median     Mean  3rd Qu.     Max. NA's
## Model1 246.6889 273.6667 304.3077 305.9077 327.9930 395.9383    0
## Model2 216.6273 240.3034 272.0816 274.0830 301.7762 381.1725    0
## Model3 186.4928 240.7172 254.6771 267.6035 301.4895 344.7352    0
## 
## RMSE 
##            Min.  1st Qu.   Median     Mean  3rd Qu.     Max. NA's
## Model1 310.6182 354.5693 386.4207 395.0818 439.4691 499.2726    0
## Model2 293.9119 325.9182 343.4973 351.2963 391.6529 446.2181    0
## Model3 227.1870 317.3216 351.6674 341.6160 374.9362 431.8287    0
## 
## Rsquared 
##              Min.   1st Qu.    Median      Mean   3rd Qu.      Max. NA's
## Model1 0.02551408 0.2207282 0.3318046 0.3216179 0.4243991 0.5242936    0
## Model2 0.15896888 0.3990622 0.4705418 0.4689345 0.5579614 0.7723264    0
## Model3 0.23019609 0.3608763 0.4689431 0.4925579 0.6378846 0.8045023    0

분석결과는 상자수염도bwplot()와 점도표dotplot()로 시각화해 각 모형의 성능을 비교할 수 있다.

resamp_l %>% bwplot()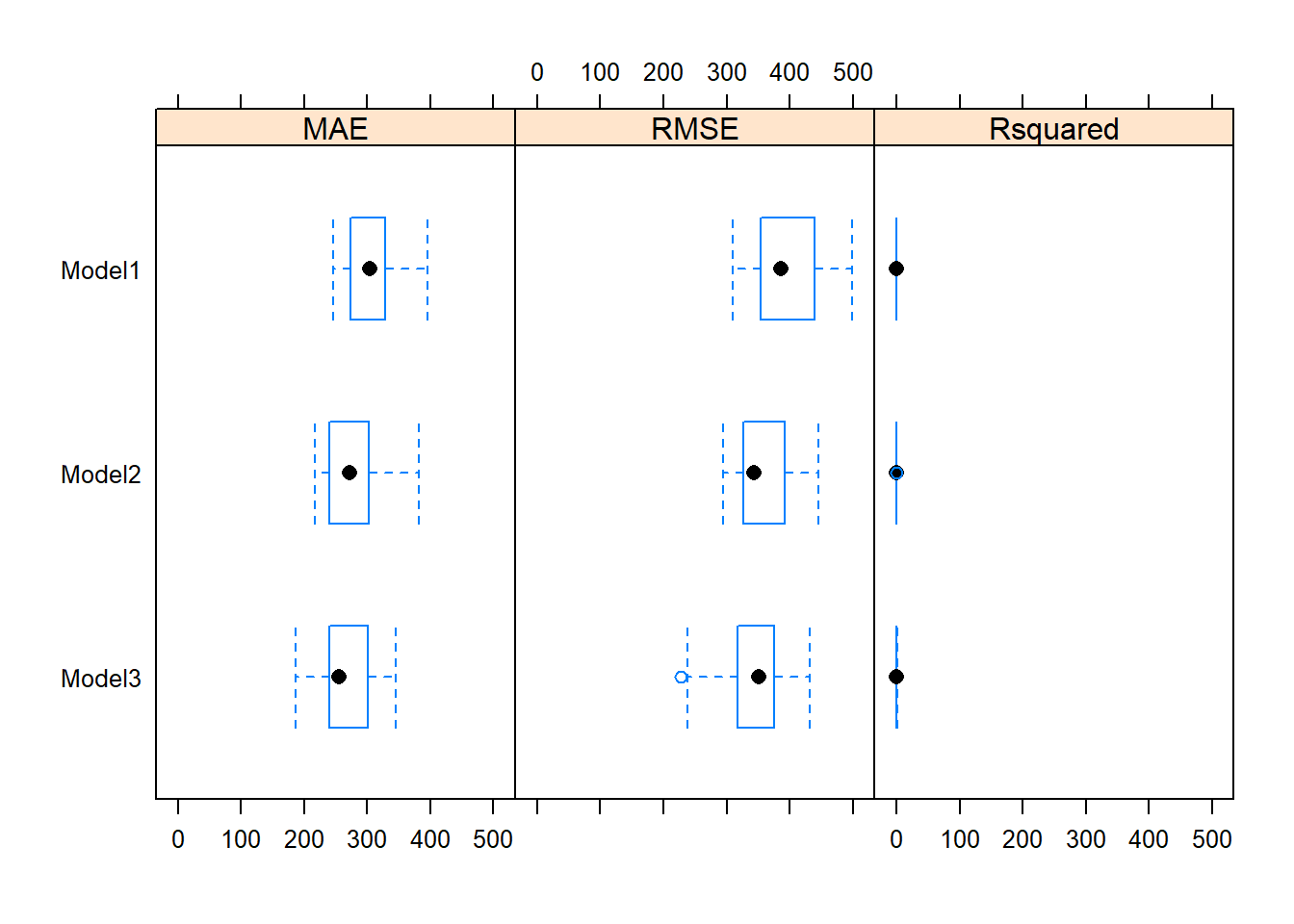

resamp_l %>% dotplot()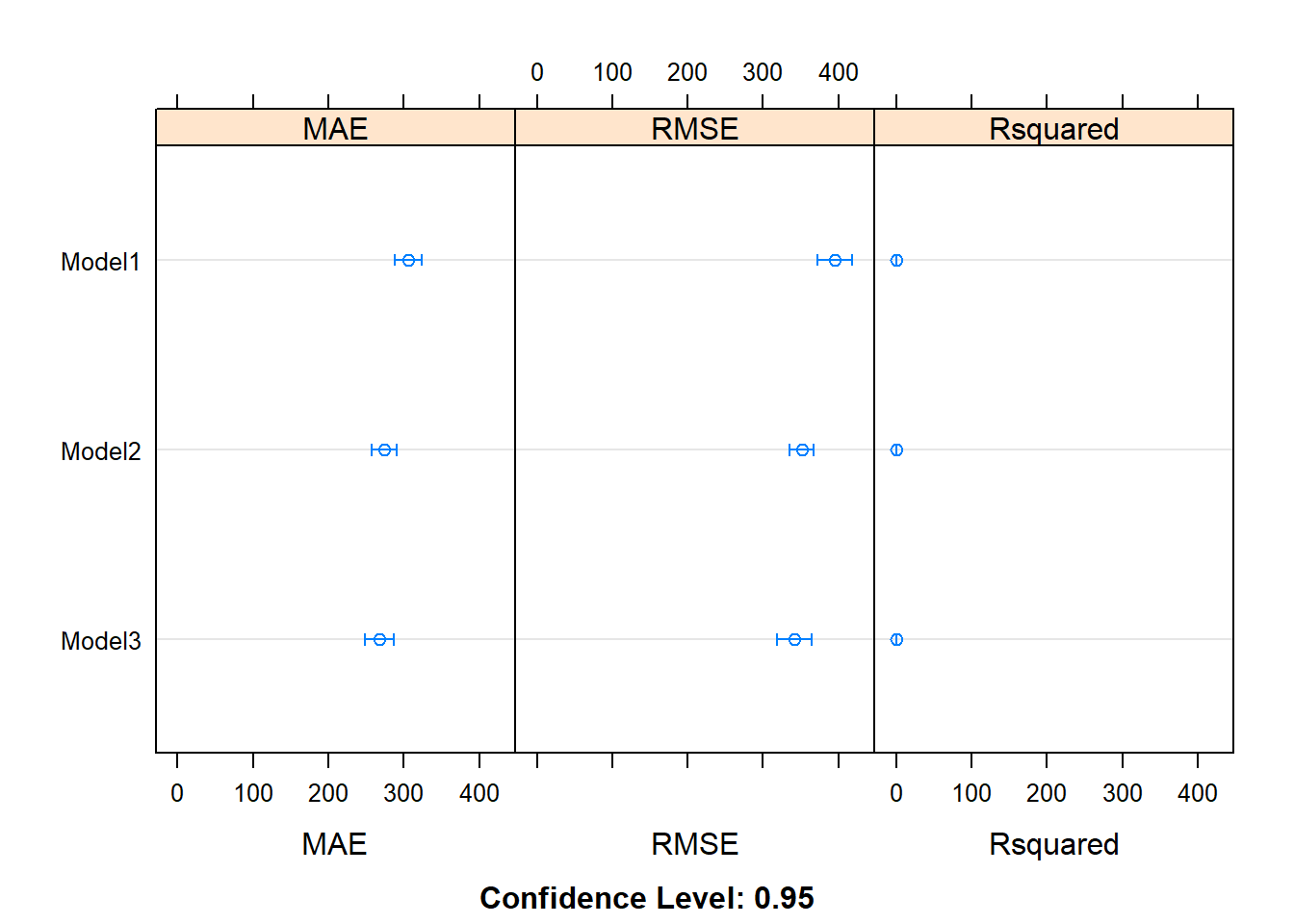

모형1보다는 모형2가, 모형2보다는 모형3의 성능이 더 좋다.

diff()함수로 \(t\)검정하여 모형의 성능 차이가 통계적으로 유의한지 확인할 수 있다.

resamp_l %>% diff() %>% summary()

## 
## Call:
## summary.diff.resamples(object = .)
## 
## p-value adjustment: bonferroni 
## Upper diagonal: estimates of the difference
## Lower diagonal: p-value for H0: difference = 0
## 
## MAE 
##        Model1  Model2  Model3
## Model1         31.82   38.30 
## Model2 0.04104          6.48 
## Model3 0.02615 1.00000       
## 
## RMSE 
##        Model1  Model2  Model3
## Model1         43.79   53.47 
## Model2 0.01202          9.68 
## Model3 0.01426 0.96599       
## 
## Rsquared 
##        Model1   Model2   Model3  
## Model1          -0.14732 -0.17094
## Model2 0.021691          -0.02362
## Model3 0.001018 1.000000

각 평가지표의 왼쪽 하단(Lower diagonal)의 값이 각 모형에 차이가 0이라는 영가설에 대한 유의확률이다.

모형1에 비해 모형2와 모형3의 성능이 통계적으로 유의하게 차이가 있다. 반면, 모형2와 모형3 사이에는 통계적으로 유의한 차이가 없다.

앞서 모형2과 모형3에 대해 표본을 교차검증하지 않고 anova()함수로 \(F\)검정을 했을 때 통계적으로 유의한 차이가 있는 것과는 다른 결과다.

SALARY -> df
df %>% lm(Salary ~ Education + Months + Gender, .) -> fit1
df %>% lm(Salary ~ Education + Months + Gender + Experience, .) -> fit2
anova(fit1, fit2)

## Analysis of Variance Table
## 
## Model 1: Salary ~ Education + Months + Gender
## Model 2: Salary ~ Education + Months + Gender + Experience
##   Res.Df      RSS Df Sum of Sq      F  Pr(>F)  
## 1     89 10603660                              
## 2     88 10070523  1    533137 4.6587 0.03362 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

10.5 종합

10.5.1 통계

10.5.2 코딩