4 분석: 회귀
c(
"rio", "psych", "psychTools", "skimr", "janitor",
"tidyverse", "tidytable", "tidymodels", "lm.beta",
"GGally", "ggforce", "gt", "mdthemes", "patchwork",
"r2symbols", "equatiomatic"
) -> pkg
sapply(pkg, function(x){
if(!require(x, ch = T)) install.packages(x)
library(x, ch = T)
})파이프2
tidyverse가 지원하는 파이프%>%를 이용하면 아래 예시처럼 간결하면서도 가독성이 좋은 코드를 작성할 수 있다.
df <- mtcars
df %>%
filter.(mpg >= 20) %>%
select.(mpg:wt) R이 내장함수로 제공하는 파이프 |>도 있지만, %>% 보다 기능이 부족하다. placeholder기능을 제공하지 않아, 회귀분석에 사용하는 lm()함수를 파이프로 코딩하려면 %>%파이프를 이용해야 한다. (R 4.2 부터는 내장 파이프 |>도 placeholder기능 제공.)
lm()
아래 코드는 lm()함수를 이용해 mtcars라는 데이터의 wt(무게: 독립변수 혹은 예측변수)로 mpg(연료효율: 종속변수 혹은 산출변수)를 예측하는 회귀분석을 하는 기술문이다. (변수(variable), 회귀분석(regression analysis)에 대해서는 추후 자세하게 배운다.)
lm(mpg ~ wt, data = mtcars)mtcars는 R에 내장된 데이터다. (단수 복수에 주의한다. 오류의 주된 원인 중 하나가 복수s누락)
~는 공식(formula)을 만들때 사용하는 기호다.
mpg ~ wt는 공식(formula)이다. “wt가 독립변수(투입요소: input 또는 predictor)로서 종속변수(산출요소: output)인 mpg를 예측한다(혹은 설명한다)”는 의미다.
아래 코드는 fit에 기술문을 할당한 다음, fit의 내용을 summary()함수로 요약해 출력하고, plot()함수로 도표를 그리라는 내용이다.
fit <- lm(formula = mpg ~ wt, data = mtcars)
summary(fit)
plot(fit) lm()등과 같은 함수의 계산결과에는 다양한 구조의 데이터가 산출되기 때문에, 이런 경우 산출값을 리스트 구조에 담는다. lm()함수는 계산 결과를 coefficients, model 등 12개의 요소로 이뤄진 리스트에 저장해 산출한다.
lm(mpg ~ wt, data = mtcars) %>% class()## [1] "lm"lm(mpg ~ wt, data = mtcars) %>% typeof()## [1] "list"lm(mpg ~ wt, data = mtcars) %>% names()## [1] "coefficients" "residuals" "effects" "rank"
## [5] "fitted.values" "assign" "qr" "df.residual"
## [9] "xlevels" "call" "terms" "model"아래 코드를 실행하면 Error in as.data.frame.default(data) : cannot coerce class ‘"formula"’ to a data.frame라는 오류가 발생한다.
df %>% lm(mpg ~ wt)data =인자에 투입할 데이터프레임 df가 파이핑됐다는 것을 .을 이용해 명시적으로 표기해야 한다.
df <- mtcars
df %>% lm(mpg ~ wt, data = .) .으로 명시적으로 파이핑하면 다음과 같은 방법으로 부분선택할 수 있다.
df %>% .$mpg
df %>% .[,1]이 방법이 유용한 이유는 여러 함수를 파이핑한 다음 부분선택해야 하는 상황이 있기 때문이다.
df %>%
filter.(mpg >= 20) %>%
select.(mpg:wt) %>%
.[1,2]lm()함수로 계산한 결과에서 계수(coefficients)만 추출해야 하는 경우, .을 이용해 파이핑해 계수만 부분선택할 수있다.
df %>%
lm(mpg ~ wt, data = .) %>%
names()
df %>%
lm(mpg ~ wt, .) %>%
.$coefficients주의!!!
아래와 같이 select()함수를 이용하면 Error in UseMethod("select_") : 클래스 "lm"의 객체에 적용된 'select_'에 사용할수 있는 메소드가 없습니다라는 오류가 발생한다.
df %>%
lm(mpg ~ wt, .) %>%
select(coefficients)lm()함수로 계산한 결과는 데이터프레임이 아닌 ’리스트(list)’라는 자료구조로 산출하는데, select()함수가 처리하는 자료구조는 데이터프레임이다.
자료의 유형과 구조를 정확하게 파악해야 하는 이유다.
4.1 선형회귀
분석을 하는 이유는 지식과 확보한 자료를 이용해 미지의 정보를 얻기 위함이다. 여기서 지식은 변수와 그 변수에 대한 분포이고, 정보는 그 변수에 대해 측정한 자료와 해석이다. 미지의 정보는 변수와 변수의 관계다.
변수와 변수의 관계는 크게 독립성(indepence), 연관성(association or dependence)/상관성(correlation), 인과성(causality)로 구분할 수 있다.
상관성은 연관성의 하위개념이므로 변수와 변수의 관계는 크게 3종으로 구분가능하다. 서로 독립적인 관계인 독립성, 서로 연관돼 있는 관계인 연관성, 그리고 한 변수가 다른 변수의 변화에 대한 원인이 되는 인과성이다.
즉, 분석의 목적은 변수와 변수의 관계가 독립적인지, 연관돼 있는지, 혹은 인과관계인지를 밝히기 위함이다.
이러한 분석의 목적을 달성하기 위한 다양한 통계모형이 있지만 가장 기본적인 모형이 선형회귀(linear regression)이다. 선형회귀는 독립변수 \(X\)가 종속변수 \(Y\)를 직선적인 형태로 예측하는 모형이다. 독립변수가 증가하는 만큼 종속변수가 증가하거나 감소하는 정도를 나타낸다.
선형회귀모형은 다음의 공식으로 나타낼수 있다.
\[Y = \alpha + \beta{X} + \epsilon\]
- \(Y\): 종속변수(결과변수 or 반응변수)
- 독립변수의 변이에 의해 설명되는 확률변수. 독립변수의 변이에 종속돼 있기에 종속변수(dependent variable)라고 한다. 독립변수의 변화의 의해 종속변수의 변이가 내생적으로(endogenously), 즉 모형의 내적 요소에 의해 결정되므로 종속변수를 내생변수(endogenous variable)라고도 한다.
- 독립변수의 변이에 의해 설명되는 확률변수. 독립변수의 변이에 종속돼 있기에 종속변수(dependent variable)라고 한다. 독립변수의 변화의 의해 종속변수의 변이가 내생적으로(endogenously), 즉 모형의 내적 요소에 의해 결정되므로 종속변수를 내생변수(endogenous variable)라고도 한다.
- \(X\): 독립변수(예측변수 or 설명변수)
- 종속변수의 변이를 설명하는 확률변수. 모형 안의 다른 변수에 의해 영향을 받지 않고 독립적이기에 독립변수(indepedent variable)라고 한다.
- 종속변수의 변이를 설명하는 확률변수. 모형 안의 다른 변수에 의해 영향을 받지 않고 독립적이기에 독립변수(indepedent variable)라고 한다.
- \(\alpha\): 절편(intercept) (alpha)
- \(X\)가 0일때 \(Y\)의 평균값.
- \(X\)가 0일때 \(Y\)의 평균값.
- \(\beta\): 기울기. 회귀계수 (beta)
- \(X\)가 한 단위 증가할 때 \(Y\)가 \(\beta\)만큼 증가 또는 감소하는 정도. 예를 들어, 일을 1시간할때마다 급여가 8000원씩 증가하면 일한 시간에 8000원을 곱하면 소득이 된다. 이 경우 회귀계수 \(\beta\)는 8000. 기울기가 0이면 \(X\)와 \(Y\) 두 변수는 서로 독립적이다.
- \(\epsilon\): 오차항 (epsilon)
- \(Y\)에 대해 \(X\)로 설명되지 않는 값.
(절편과 기울기값을 모두 계수(coefficient)라고 한다.)
mtcars데이터셋에서 차량의 무게(wt)를 독립변수로 하여 연비(mpg)를 종속변수로 하는 회귀모형을 구성하면 다음과 같다.
mtcars %>% lm(mpg ~ wt, .) %>% extract_eq()\[ \operatorname{mpg} = \alpha + \beta_{1}(\operatorname{wt}) + \epsilon \]
위 회귀모형을 다음과 같이 적합(fit)하여 다음과 같이 회귀계수를 계산할 수 있다.
mtcars %>% lm(mpg ~ wt, .) ##
## Call:
## lm(formula = mpg ~ wt, data = .)
##
## Coefficients:
## (Intercept) wt
## 37.285 -5.344기울기가 약 -5.34이므로 무게가 1단위 증가할때 연비는 약 5.34감소한다. (절편(intercept)이 37.28이므로 자동차의 무게가 0일때 연비는 37.28이라고 할수 있으나, 자동차 무게가 0인 경우는 없으므로 그 의미를 해석하지 않는다.)
mtcars %>% lm(mpg ~ wt, .) %>% class()## [1] "lm"mtcars %>% lm(mpg ~ wt, .) %>% typeof()## [1] "list"회귀모형을 lm() 함수로 적합한 결과의 자료구조는 리스트다. tidymodels패키지에 포함돼 있는 broom패키지의 tidy()함수를 이용하면 분석에 편리한 데이터프레임(정확하게는 tibble형식의 데이터프레임)으로 생성할 수 있다.
mtcars %>% lm(mpg ~ wt, .) %>% tidy()## # A tibble: 2 x 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 37.3 1.88 19.9 8.24e-19
## 2 wt -5.34 0.559 -9.56 1.29e-10term: 독립변수(Intercept): 절편 \(\alpha\)estimate: 회귀계수(기울기 \(\beta\))std.error: 표준오차. 기울기의 오차. 측정값이 회귀계수로 설명되지 않는 정도.
회귀계수와 상관계수 선형회귀모형에서 추정된 기울기의 계수(\(\widehat{\beta}\))는 상관계수 및 X와 Y의 표준편차의 증가에 비례한다.
\[\widehat{\beta} = X와 Y의 상관관계(\rho) \times \frac{Y의 표준편차}{X의 표준편차}\]
양의 상관관계는 양의 기울기, 음의 상관관계는 음의 기울기에 해당한다.
기울기 계수는 \(X\)의 1표준편차 증가할때 \(Y\)의 \(\rho\)표준편차 단위의 증가와 관련돼 있다. 예를 들어, 상관관계가 0.5인 경우 \(X\)의 표준편차가 1 증가하면 \(Y\)의 표준편차는 0.5 증가한다. (\(\rho\)\(P\)(rho) = rR)
4.1.1 회귀선
측정한 자료에는 변수의 값만 포함돼 있으므로 \(\alpha\)와 \(\beta\)는 자료에서 추정(예측)해야 한다.
추정값(예측값 or 근사값)은 계수에 widehat(\(\widehat{}\))을 쒸워 표기한다. \(\alpha\)의 추정값은 \(\widehat{\alpha}\), \(\beta\)의 추정값은 \(\widehat{\beta}\)로 표기한다.
\(\alpha\)와 \(\beta\)의 추정값으로 회귀선(regrssion line)을 구성한다.
회귀선을 시각화해보자.
mtcars %>%
ggplot(aes(wt, mpg)) +
geom_point() +
geom_smooth(method = lm, se = F) +
labs(title = "차량무게의 연비에 대한 선형회귀모형") +
theme(plot.title = element_text(size = 17))## `geom_smooth()` using formula 'y ~ x'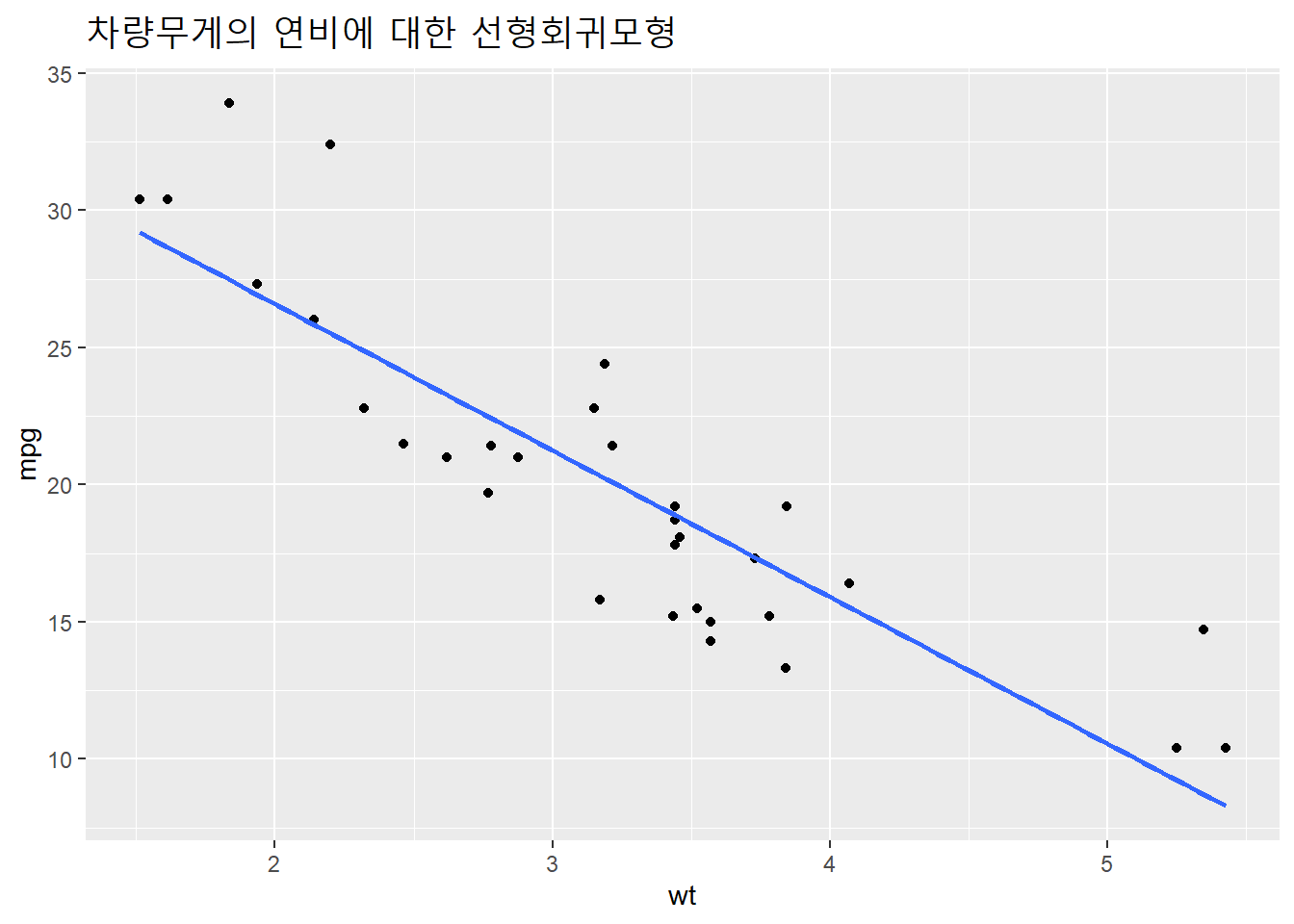
가상의 데이터셋을 만들어 회귀선을 구성해보자.
df1 <- data.frame(x = c(1, 2, 3),
y = c(1, 2, 3))
df2 <- data.frame(x = c(1, 2, 1, 4),
y = c(1, 2, 2, 2))
df3 <- data.frame(x = c(1, 3, 1, 3),
y = c(1, 1, 3, 3))
df4 <- data.frame(x = c(1, 2, 3, 4),
y = c(1, 2, 3, 2))df1 %>% ggplot(aes(x, y)) +
xlim(0,5) + ylim(0,4) +
geom_point(size = 3, color = "red")
df2 %>% ggplot(aes(x, y)) +
xlim(0,5) + ylim(0,4) +
geom_point(size = 3, color = "red")
df3 %>% ggplot(aes(x, y)) +
xlim(0,5) + ylim(0,4) +
geom_point(size = 3, color = "red")
df4 %>% ggplot(aes(x, y)) +
xlim(0,5) + ylim(0,4) +
geom_point(size = 3, color = "red") 같은 내용이 반복됐으니 반복문으로 간략하게 표현하자. 각 점의 위치를 가장 잘 반영할 수 있는 최적의 직선을 그어보자.
dfl <- list(df1, df2, df3, df4)
lapply(dfl, function(dfx){
dfx %>% ggplot(aes(x, y)) +
xlim(0,5) + ylim(0,4) +
geom_point(size = 3, color = "red")
}) -> p
# patchwork패키지
p[[1]] + p[[2]] + p[[3]] + p[[4]] +
plot_annotation(
title = "각 점을 잇는 최적화된 직선을 그어보자",
tag_levels = "A") 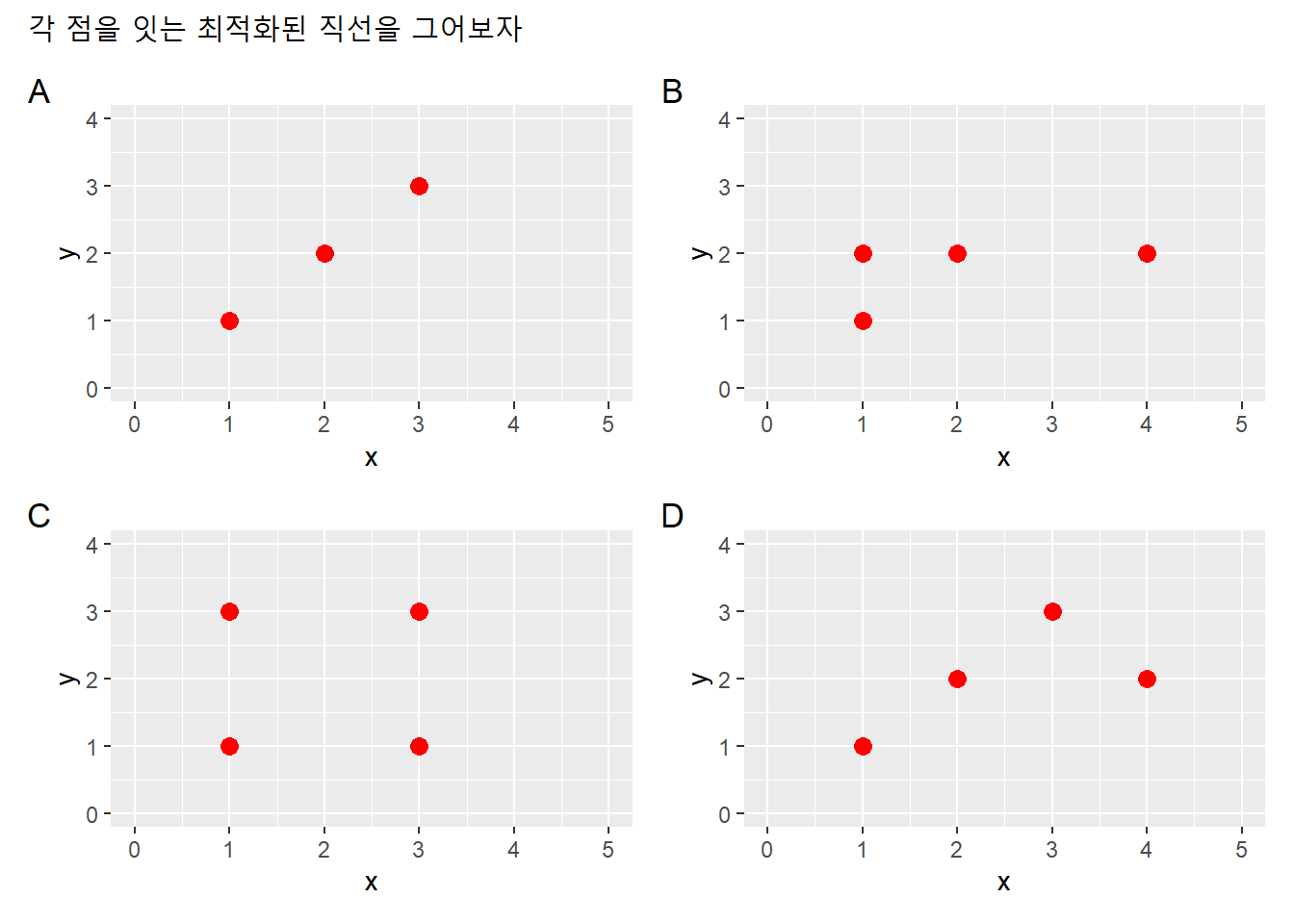
다음과 같이 최적의 직선을 구성할 수 있다.
dfl <- list(df1, df2, df3, df4)
lapply(dfl, function(dfx){
dfx %>% ggplot(aes(x, y)) +
xlim(0,5) + ylim(0,4) +
geom_point(size = 3, color = "red") +
geom_smooth(method = lm, se = F)
}) -> p
p[[1]] + p[[2]] + p[[3]] + p[[4]] +
plot_annotation(
title = "각 점을 잇는 최적화된 직선을 그어보자",
tag_levels = "A") ## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'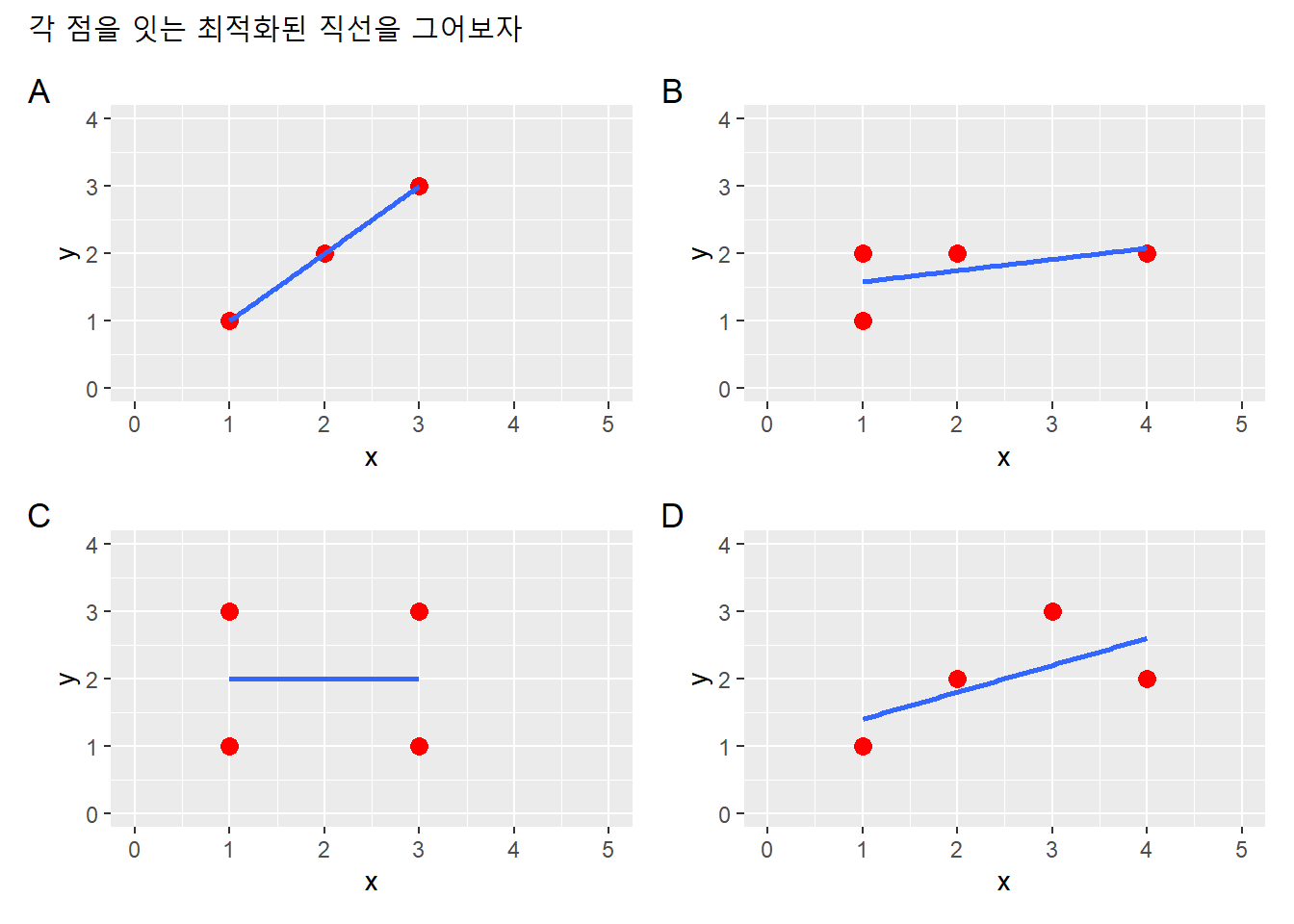
4.1.2 잔차
회귀선을 구성하면 독립변수 \(X\)에 대한 종속변수 \(Y\)의 값을 얻을 수 있다. 독립변수 \(X\)의 특정 값 \(x\)가 주어지면, \(\alpha\)와 \(\beta\)를 이용해 특정 값 \(x\)에 대한 종속변수의 예측값(predicted value) 또는 적합값(fitted value)을 구할수 있다. 예측된 값(즉, 추정된 근사값)이므로 \(\widehat{Y}\)로 표기한다.
\[\widehat{Y} = \widehat{\alpha} + \widehat{\beta}{x}\] 독립변수 \(X\)에 대한 종속변수 \(Y\)의 값과 특정 값 \(x\)에 대한 예측값(혹은 측정값)은 같을 수도 있고 다를 수도 있다. 이 차이를 잔차(residual) 또는 예측오차(predicted error)라고 한다. 오차항\(\epsilon\)의 추정값이다. \(\widehat{\epsilon}\)로 표기한다.
\[\widehat{\epsilon} = Y - \widehat{Y}\]
mtcars데이터셋에서 차량의 무게과 연비의 관계에 대해 회귀모형을 적합한 뒤 잔차를 구해보자. broom패키지의 augment()함수를 이용한다.
mtcars %>% lm(mpg ~ wt, .) %>%
augment() %>% head() %>%
gt() %>%
tab_header("측정값, 예측값, 잔차") %>%
fmt_number(-.rownames, decimals = 2)| 측정값, 예측값, 잔차 | ||||||||
|---|---|---|---|---|---|---|---|---|
| .rownames | mpg | wt | .fitted | .resid | .hat | .sigma | .cooksd | .std.resid |
| Mazda RX4 | 21.00 | 2.62 | 23.28 | −2.28 | 0.04 | 3.07 | 0.01 | −0.77 |
| Mazda RX4 Wag | 21.00 | 2.88 | 21.92 | −0.92 | 0.04 | 3.09 | 0.00 | −0.31 |
| Datsun 710 | 22.80 | 2.32 | 24.89 | −2.09 | 0.06 | 3.07 | 0.02 | −0.71 |
| Hornet 4 Drive | 21.40 | 3.21 | 20.10 | 1.30 | 0.03 | 3.09 | 0.00 | 0.43 |
| Hornet Sportabout | 18.70 | 3.44 | 18.90 | −0.20 | 0.03 | 3.10 | 0.00 | −0.07 |
| Valiant | 18.10 | 3.46 | 18.79 | −0.69 | 0.03 | 3.10 | 0.00 | −0.23 |
주요 열의 의미는 다음과 같다.
mpg: 종속변수의 측정값wt: 독립변수의 특정 값 \(x\).fitted: 예측값 또는 적합값.resid: 잔차(residual). 측정값과 적합값의 차이
잔차를 시각화해보자. 편의를 위해 6행 2열로 된 가상의 데이터셋을 이용하자.
data.frame(iv = c(1, 2, 3, 4, 5, 6),
dv = c(3, 3, 1, 2, 4, 2)) -> df
df %>% ggplot(aes(iv, dv)) +
xlim(0, 7) + ylim(1, 5) +
geom_point(color = "red", size = 3) +
geom_smooth(method = lm, se = F)## `geom_smooth()` using formula 'y ~ x'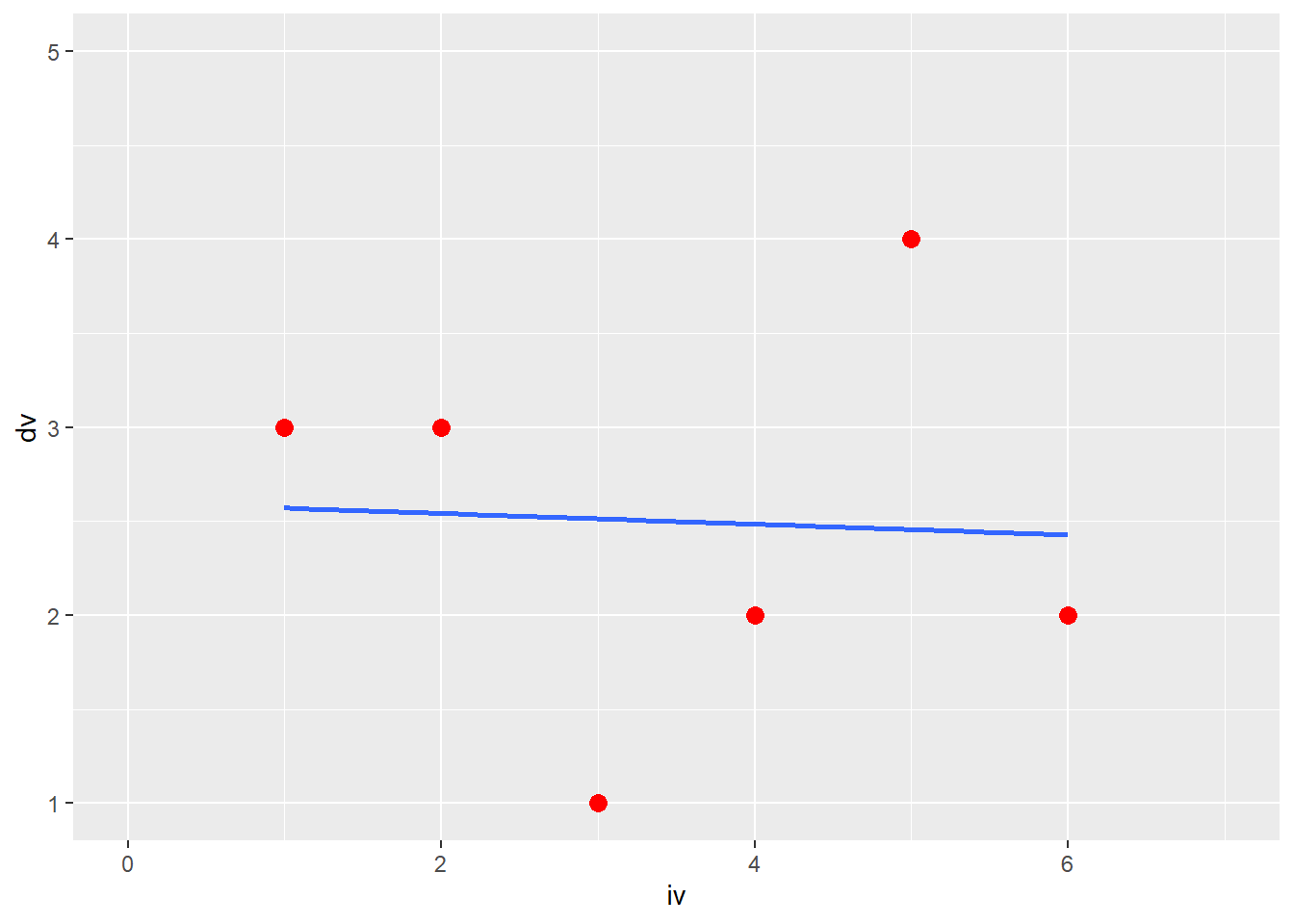
잔차를 구해보자.
df %>% lm(dv ~ iv, .) %>% augment() -> res
res## # A tibble: 6 x 8
## dv iv .fitted .resid .hat .sigma .cooksd .std.resid
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 3 1 2.57 0.429 0.524 1.30 0.155 0.530
## 2 3 2 2.54 0.457 0.295 1.32 0.0453 0.465
## 3 1 3 2.51 -1.51 0.181 0.946 0.226 -1.43
## 4 2 4 2.49 -0.486 0.181 1.32 0.0232 -0.458
## 5 4 5 2.46 1.54 0.295 0.838 0.516 1.57
## 6 2 6 2.43 -0.429 0.524 1.30 0.155 -0.530측정값과 적합값을 산점도에 표시해보자.
df %>% ggplot(aes(iv, dv)) +
xlim(0, 7) + ylim(1, 5) +
# 측정값의 산점도
geom_point(color = "red", size = 3) +
geom_smooth(method = lm, se = F) +
geom_text(aes(label = dv),
nudge_x = -.2) +
# 적합값(예측값)의 산점도
geom_point(aes(res$iv, res$.fitted),
color = "blue", size = 3) +
geom_text(aes(y = round(res$.fitted, 2),
label = round(res$.fitted, 2)),
nudge_x = -.2, nudge_y = -.2) +
labs(title = "측정값(빨간 점)과 적합값(파란 점)") ## `geom_smooth()` using formula 'y ~ x'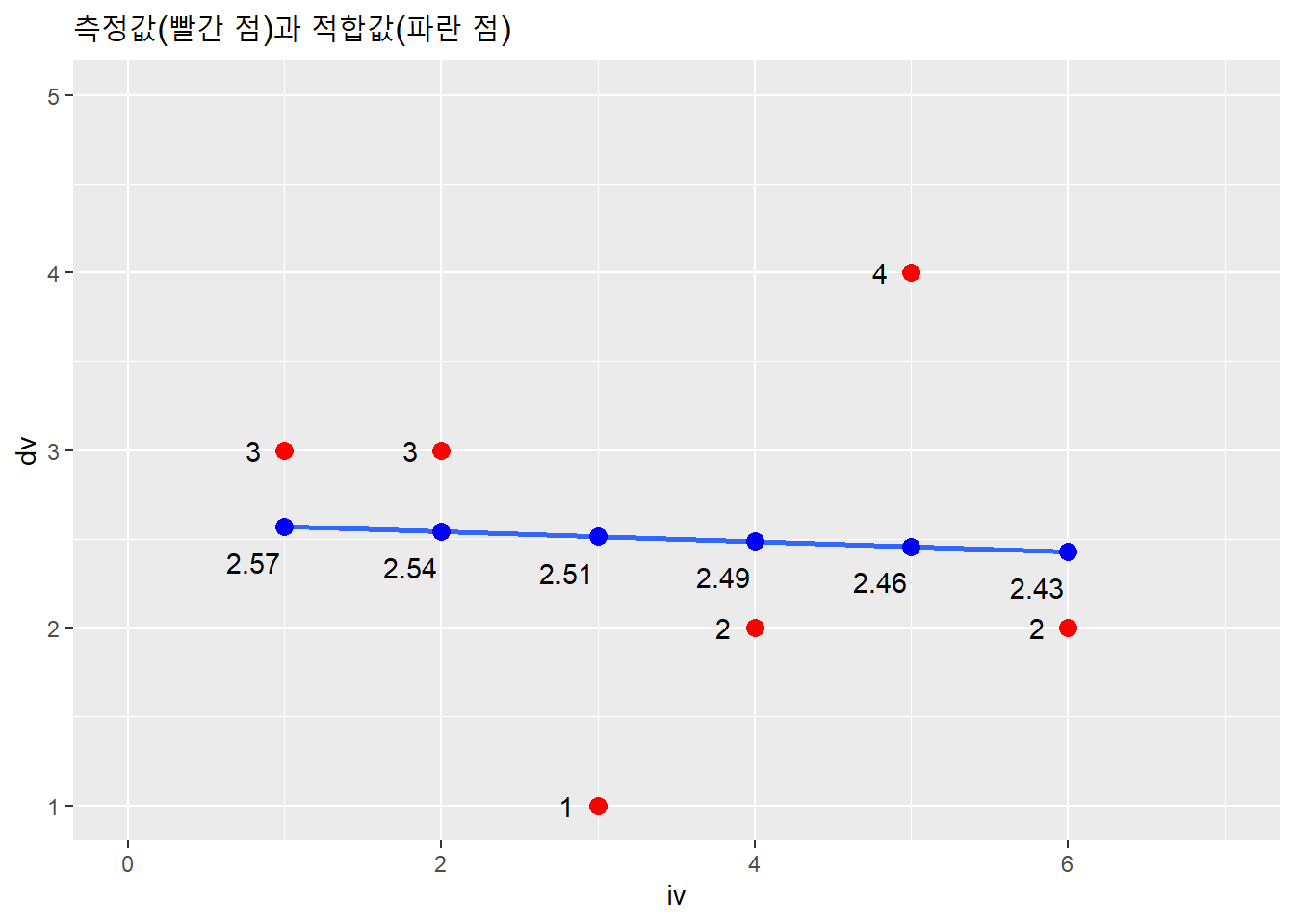
측정값과 적합값을 연결해 잔차를 표시해보자.
df %>% ggplot(aes(iv, dv)) +
xlim(0, 7) + ylim(1, 5) +
# 측정값의 산점도
geom_point(color = "red", size = 3) +
geom_smooth(method = lm, se = F) +
geom_text(aes(label = dv),
nudge_x = -.2) +
# 적합값(예측값)의 산점도
geom_point(aes(res$iv, res$.fitted),
color = "blue", size = 3) +
geom_text(aes(y = res$.fitted,
label = round(res$.fitted, 2)),
nudge_x = -.2, nudge_y = -.2) +
# 측정값과 예측값의 차이
geom_segment(aes(x = res$iv, y = res$dv,
xend = res$iv, yend = res$.fitted),
color = "#4daf4a", size = 1) +
labs(title = "잔차: 측정값과 적합값의 차이(녹색 선)") ## `geom_smooth()` using formula 'y ~ x'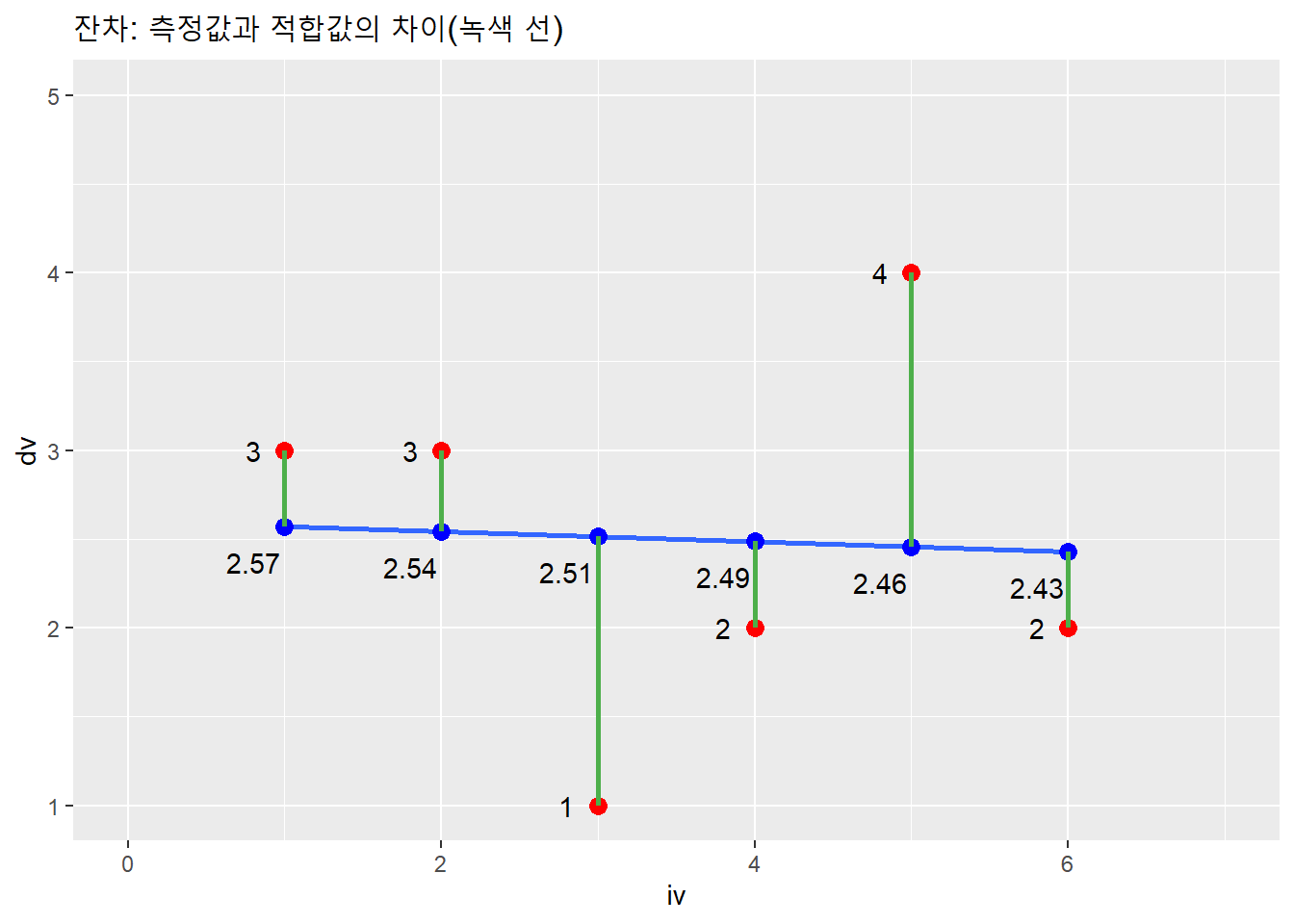
즉, 회귀선은 녹색선의 합(잔차제곱의 합)이 최소값을 이루도록 구성한 선이다. 이런 이유로 회귀선을 최우량적합선(line of best fit)이라고 한다. 예측오차의 크기를 최소화하도록 구성하기 때문이다.
이처럼 회귀선의 절편과 기울기값을 추정하기 위해 사용하는 방법을 최소제곱법(or 최소자승법: least square)이리고 한다. 잔차제곱합(SSR: Sum of Squared Residual)을 최소화하는 방법이기 때문이다. 잔차를 제곱하는 이유는 측정값과 예측값의 차이가 음수와 양수 모두 포함돼 있기 때문이다. (잔차(residual)는 측정 오차(error)이므로 잔차제곱합을 SSE(Sum of Squared Error)로 기술한 교재도 있다.)
- SSR(Sum of Squared Residual): 잔차제곱합. 독립변수 \(X\)에 의해 설명되지 않는 종속변수 \(Y\)의 변동을 나타낸다.
이런 식으로 잔차제곱의 합을 통해 최소제곱합을 구하는 회귀분석 방법을 최소자승회귀분석(Least Squares Regression) 혹은 OLS(Ordinary Least Squares: 표준 회귀분석)이라고 한다.
4.1.3 모형적합도
회귀모형의 성능은 모형이 측정한 자료에 어느 정도 잘 맞는지를 나타낸다. 즉, 독립변수 \(X\)의 변동을 통해 종속변수 \(Y\)의 변동을 설명할 수 있는 정도로 판단할 수 있다.
종속변수의 변동은 종속변수 측정값과 종속변수 평균의 차이다.
\[Y - \overline{Y}\] 총변동은 이 차이를 제곱해 모두 더한 값(총제곱합)이다. 총제곱합(TSS: Total Sum of Squares)으로 나타낸다. (통계 교재 중 SST(Sum of Squares Total)로 기술한 사례도 있다.)
\[TSS = \sum_{i = 1}^n(Y_i - \overline{Y})^2\]
이 총변동에는 회귀모형으로 설명되는 부분과 설명되지 않는 부분이 있다. 설명되는 부분은 종속변수 평균과 회귀선상 적합값 사이의 차이다. 설명되지 않는 부분은 측정값과 회귀선상 적합값 사이의 차이 즉, 잔차다.
잔차가 크다는 것은 측정값과 예측값의 차이가 크다는 것이고, 잔차가 작다면 측정값과 예측값의 차이가 작다는 의미다. 따라서 잔차제곱의 합(SSR)으로 회귀모형의 성능(회귀모형이 측정한 값을 얼마나 잘 예측하는지)을 판단할 수 있다.
따라서 총제곱합(TSS)에서 잔차제곱합(SSR: 모형의 독립변수가 종속변수에 대해 설명하지 못하는 정도)을 빼면 회귀모형이 성능을 측정할 수 있다. 이런 식으로 회귀모형이 측정한 값을 예측하는 정도(모형이 자료에 잘 맞는 정도)를 모형적합도(model fit)라고 한다.
모형적합도를 평가하는 지표 중 널리 사용되는 게 \(R^2\)(결정계수: coefficient of determination)다.
- 결정계수(\(R^2\)): 모형적합도의 척도로서 독립변수가 설명하는 종속변수의 총 변동비율이다. \(R^2\)의 범위는 0에서 1까지이다.
결정계수를 구하는 공식은 다음과 같다.
\[R^2 = \frac{TSS - SSR}{TSS} = 1 - \frac{SSR}{TSS}\]
결정계수는 R기본함수 summary()로 구할수 있다.
df %>% lm(dv ~ iv, .) %>% summary()##
## Call:
## lm(formula = dv ~ iv, data = .)
##
## Residuals:
## 1 2 3 4 5 6
## 0.4286 0.4571 -1.5143 -0.4857 1.5429 -0.4286
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.60000 1.09022 2.385 0.0756 .
## iv -0.02857 0.27994 -0.102 0.9236
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.171 on 4 degrees of freedom
## Multiple R-squared: 0.002597, Adjusted R-squared: -0.2468
## F-statistic: 0.01042 on 1 and 4 DF, p-value: 0.9236Call: 회귀모형Residuals: 측정값별 잔차에 대한 통계치.Coefficients: 계수Estimate: 회귀계수. 기울기 \(\beta\).Std. Error: 표준오차. 기울기의 오차. 회귀선으로 설명되지 않는 정도. 결정계수가 0.09이므로 이 회귀모형은 종속변수를 9% 설명한다.Multiple R-squared: 결정계수(\(R^2\))
결정계수는 리스트 요소의 이름으로 부분선택해 벡터로 추출할 수 있다.
df %>% lm(dv ~ iv, .) %>%
summary() %>% .$r.squaredsummary(lm(dv ~ iv, df))$r.squared데이터프레임으로 출력하려면 broom패키지의 glance()함수를 이용한다.
df %>% lm(dv ~ iv, .) %>% glance() %>%
gt() %>%
tab_header("glance()함수로 본 회귀모형의 결정계수") %>%
fmt_number(columns = -df, decimals = 2)| glance()함수로 본 회귀모형의 결정계수 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| r.squared | adj.r.squared | sigma | statistic | p.value | df | logLik | AIC | BIC | deviance | df.residual | nobs |
| 0.00 | −0.25 | 1.17 | 0.01 | 0.92 | 1 | −8.24 | 22.49 | 21.86 | 5.49 | 4.00 | 6.00 |
잔차제곱합을 달리한 가상의 데이터셋 3종을 만들어 회귀계수와 결정계수가 어떻게 변하는지 살펴보자.
# SSR이 0인 동질집단
nn <- 10
set.seed(52)
noise_sd <- 0
noise <- rnorm(nn, 20, noise_sd) %>% as.integer()
iv <- seq(1, by = 1, length.out = nn)
dv <- seq(100, by = 10, length.out = nn) + noise
data.frame(X = iv, Y = dv) -> df_zero
# SSR이 작은 분산집단1
set.seed(52)
noise_sd <- 20
noise <- rnorm(nn, 20, noise_sd) %>% as.integer()
iv <- seq(1, by = 1, length.out = nn)
dv <- seq(100, by = 10, length.out = nn) + noise
data.frame(X = iv, Y = dv) -> df_small
# SSR이 큰 분산집단2
set.seed(52)
noise_sd <- 100
noise <- rnorm(nn, 20, noise_sd) %>% as.integer()
iv <- seq(1, by = 1, length.out = nn)
dv <- seq(100, by = 10, length.out = nn) + noise
data.frame(X = iv, Y = dv) -> df_big
# 각 데이터프레임 열결합
df_zero %>%
#왼쪽 데이터프레임기준 X열을 기준으로 결합. 같은 열이름 복제.
left_join(df_small, by = "X", copy = T) %>%
left_join(df_big, by = "X", copy = T) -> df
df비슷한 작업을 반복했으니 반복문으로 코드를 단순화하자.
# 데이터셋 행 개수
nn <- 10
# 데이터셋 분산성변이(표준편차)
noise_sd <- c(0, 20, 100)
iv <- 1:nn
df <- data.frame(X = iv) # left_join()의 기준열 마련
for(i in seq_along(noise_sd)) {
set.seed(52) # rnorm 초기값을 매번 같은 수로 발생
noise <- rnorm(nn, 20, noise_sd[i]) %>% as.integer()
dv <- seq(100, by = 10, length.out = nn) + noise
output <- data.frame(
X = iv,
Y = dv
)
df <- left_join(df, output, by = "X", copy = T)
}
c("X", "Yzro", "Ysml", "Ybig") -> colnames(df)
df## X Yzro Ysml Ybig
## 1 1 120 100 22
## 2 2 130 122 91
## 3 3 140 166 270
## 4 4 150 169 245
## 5 5 160 118 -53
## 6 6 170 191 276
## 7 7 180 154 50
## 8 8 190 200 244
## 9 9 200 180 99
## 10 10 210 225 2883개의 종속변수에 대해 각각 회귀분석을 해 회귀계수와 결정계수를 구하자.
# 회귀계수
df %>% lm(Yzro ~ X, .) %>% tidy() %>% .[1:2]
df %>% lm(Ysml ~ X, .) %>% tidy() %>% .[1:2]
df %>% lm(Ybig ~ X, .) %>% tidy() %>% .[1:2]
# 결정계수
df %>% lm(Yzro ~ X, .) %>% glance() %>% .[1]
df %>% lm(Ysml ~ X, .) %>% glance() %>% .[1]
df %>% lm(Ybig ~ X, .) %>% glance() %>% .[1] 회귀계수와 결정계수를 하나의 표에 표시하자. 상하 방향으로 데이터프레임을 결합하려면 열의 개수가 일치해야 한다. 결정계수 데이터프레임을 2열의 long-form으로 변경해 행결합한다.
df %>% lm(Yzro ~ X, .) %>% tidy() %>% .[1:3]## Warning in summary.lm(x): essentially perfect fit: summary may be unreliable## # A tibble: 2 x 3
## term estimate std.error
## <chr> <dbl> <dbl>
## 1 (Intercept) 110 1.46e-14
## 2 X 10 2.35e-15bind_rows(
df %>% lm(Yzro ~ X, .) %>% tidy() %>% .[1:3],
data.frame(
term = " - 결정계수(R2)",
estimate = (lm(Yzro ~ X, df) %>% summary() %>% .$r.squared),
std.error = NA)
) -> df1; df1## Warning in summary.lm(x): essentially perfect fit: summary may be unreliable## Warning in summary.lm(.): essentially perfect fit: summary may be unreliable## # A tibble: 3 x 3
## term estimate std.error
## <chr> <dbl> <dbl>
## 1 "(Intercept)" 110 1.46e-14
## 2 "X" 10 2.35e-15
## 3 " - 결정계수(R2)" 1 NAbind_rows(
df %>% lm(Yzro ~ X, .) %>% tidy() %>% .[1:3],
data.frame(
term = " - 결정계수(R2)",
estimate = (lm(Yzro ~ X, df) %>% summary() %>% .$r.squared),
std.error = NA) # 열의 개수 맞추기 위해 NA열 추가.
) -> df1; df1
bind_rows(
df %>% lm(Ysml ~ X, .) %>% tidy() %>% .[1:3],
data.frame(
term = " - 결정계수(R2)",
estimate = (lm(Ysml ~ X, df) %>% summary() %>% .$r.squared),
std.error = NA) # 열의 개수 맞추기 위해 NA열 추가.
) -> df2; df2
bind_rows(
df %>% lm(Ybig ~ X, .) %>% tidy() %>% .[1:3],
data.frame(
term = " - 결정계수(R2)",
estimate = (lm(Ybig ~ X, df) %>% summary() %>% .$r.squared),
std.error = NA) # 열의 개수 맞추기 위해 NA열 추가.
) -> df3; df33개의 데이터프레임을 좌우방향으로 결합해 표 하나로 구성한다.
df1 %>%
left_join(df2, copy = T, by = "term") %>%
left_join(df3, copy = T, by = "term")비슷한 작업을 반복했으므로 반복문으로 단순화한다.
iv <- c("X", "Yzro", "Ysml", "Ybig")[1]
dv <- c("X", "Yzro", "Ysml", "Ybig")[2:4]
output <- list()
for(i in seq_along(dv)){
fml <- paste(dv[i], "~", iv) # 회귀식. 종속변수 반복
bt <- lm(fml, df) %>% tidy() %>% .[1:3] # 변수명과 기울기
rs <- data.frame(
term = " - 결정계수(R2):",
estimate = summary(lm(fml, df))$r.squared,
std.error = NA) # 열의 개수 맞추기 위해 NA열 추가.
op <- bind_rows(bt, rs)
output <- list(output, op)
}## Warning in summary.lm(x): essentially perfect fit: summary may be unreliable## Warning in summary.lm(lm(fml, df)): essentially perfect fit: summary may be
## unreliableoutput## [[1]]
## [[1]][[1]]
## [[1]][[1]][[1]]
## list()
##
## [[1]][[1]][[2]]
## # A tibble: 3 x 3
## term estimate std.error
## <chr> <dbl> <dbl>
## 1 "(Intercept)" 110 1.46e-14
## 2 "X" 10 2.35e-15
## 3 " - 결정계수(R2):" 1 NA
##
##
## [[1]][[2]]
## # A tibble: 3 x 3
## term estimate std.error
## <chr> <dbl> <dbl>
## 1 "(Intercept)" 105. 17.1
## 2 "X" 10.5 2.76
## 3 " - 결정계수(R2):" 0.643 NA
##
##
## [[2]]
## # A tibble: 3 x 3
## term estimate std.error
## <chr> <dbl> <dbl>
## 1 "(Intercept)" 84.4 86.4
## 2 "X" 12.5 13.9
## 3 " - 결정계수(R2):" 0.0917 NA컨테이너로 만든 리스트에 리스트를 추가했기 때문에, 리스트의 구조가 복잡하다.
output[[1]][[1]][[2]]## # A tibble: 3 x 3
## term estimate std.error
## <chr> <dbl> <dbl>
## 1 "(Intercept)" 110 1.46e-14
## 2 "X" 10 2.35e-15
## 3 " - 결정계수(R2):" 1 NAoutput[[1]][[2]]## # A tibble: 3 x 3
## term estimate std.error
## <chr> <dbl> <dbl>
## 1 "(Intercept)" 105. 17.1
## 2 "X" 10.5 2.76
## 3 " - 결정계수(R2):" 0.643 NAoutput[[2]]## # A tibble: 3 x 3
## term estimate std.error
## <chr> <dbl> <dbl>
## 1 "(Intercept)" 84.4 86.4
## 2 "X" 12.5 13.9
## 3 " - 결정계수(R2):" 0.0917 NA리스트에서 각 데이터프레임을 부분선택해 데이터프레임으로 결합하자.
output[[1]][[1]][[2]] %>%
left_join(output[[1]][[2]], by = "term", copy = T) %>%
left_join(output[[2]], by = "term", copy = T) -> df_fit
df_fit## # A tibble: 3 x 7
## term estimate.x std.error.x estimate.y std.error.y estimate std.error
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 "(Intercept)" 110 1.46e-14 105. 17.1 84.4 86.4
## 2 "X" 10 2.35e-15 10.5 2.76 12.5 13.9
## 3 " - 결정계~ 1 NA 0.643 NA 0.0917 NA표 형식에 맞춰 구성하자.
df_fit %>%
gt() %>%
tab_header("SSR을 달리한 회귀모형 3종 비교") %>%
fmt_number(columns = -term, decimals = 2) %>%
fmt_missing(columns = -term) %>%
cols_label(
term = md("_IV_"),
estimate.x = md("_B_"),
std.error.x = md("_SE_"),
estimate.y = md("_B_"),
std.error.y = md("_SE_"),
estimate = md("_B_"),
std.error = md("_SE_")
) %>%
tab_spanner(
label = "Yzro", columns = 2:3) %>%
tab_spanner(
label = "Ysml", columns = 4:5) %>%
tab_spanner(
label = "Ybig", columns = 6:7) | SSR을 달리한 회귀모형 3종 비교 | ||||||
|---|---|---|---|---|---|---|
| IV | Yzro | Ysml | Ybig | |||
| B | SE | B | SE | B | SE | |
| (Intercept) | 110.00 | 0.00 | 104.87 | 17.12 | 84.40 | 86.36 |
| X | 10.00 | 0.00 | 10.48 | 2.76 | 12.51 | 13.92 |
| - 결정계수(R2): | 1.00 | — | 0.64 | — | 0.09 | — |
Ysml과 Ybig는 종속변수의 변동성을 늘렸지만 기울기와 절편은 Yzro와 비슷하다. 차이는 표준오차(SE)와 결정계수다.
분산성을 늘려 잔차가 증가했고, 이로인해 SSR(잔체제곱합)이 커졌다. 즉, 회귀모형으로 설명되지 않는 값이 커졌다. 그만큼 주어진 회귀모형에서 종속변수에 대해 독립변수로 설명하지 못하는 변수의 영향이 크다는 의미다. 즉, 이 사례에서 Ybig모형에는 종속변수에 대한 설명력이 모형에 투입한 독립변수 외에 설명력이 더 큰 다른 제3의 변수가 있다는 의미다.
세 모형을 하나의 도표로 시각화해보자. 이를 위해서는 3개 열에 나뉘어 있는 종속변수를 pivot_longer()함수로 하나의 열로 피보팅 한다. 즉, long-form으로 바꿔야 한다.
names(df)## [1] "X" "Yzro" "Ysml" "Ybig"2열부터 4열까지의 열을 하나의 열로 피보팅한다.
df %>% pivot_longer(2:4,
names_to = "DVname",
values_to = "Y") -> df
head(df)## # A tibble: 6 x 3
## X DVname Y
## <int> <chr> <dbl>
## 1 1 Yzro 120
## 2 1 Ysml 100
## 3 1 Ybig 22
## 4 2 Yzro 130
## 5 2 Ysml 122
## 6 2 Ybig 91df %>%
ggplot(aes(X, Y, color = DVname, shape = DVname)) +
xlim(0, 11) + ylim(-60, 350) +
geom_point(size = 3, alpha = .5) +
geom_smooth(method = lm, se = F, fullrange = T) +
labs(x = "독립변수", y = "종속변수",
title = "SSR을 달리한 회귀모형 3종 산점도와 회귀선")## `geom_smooth()` using formula 'y ~ x'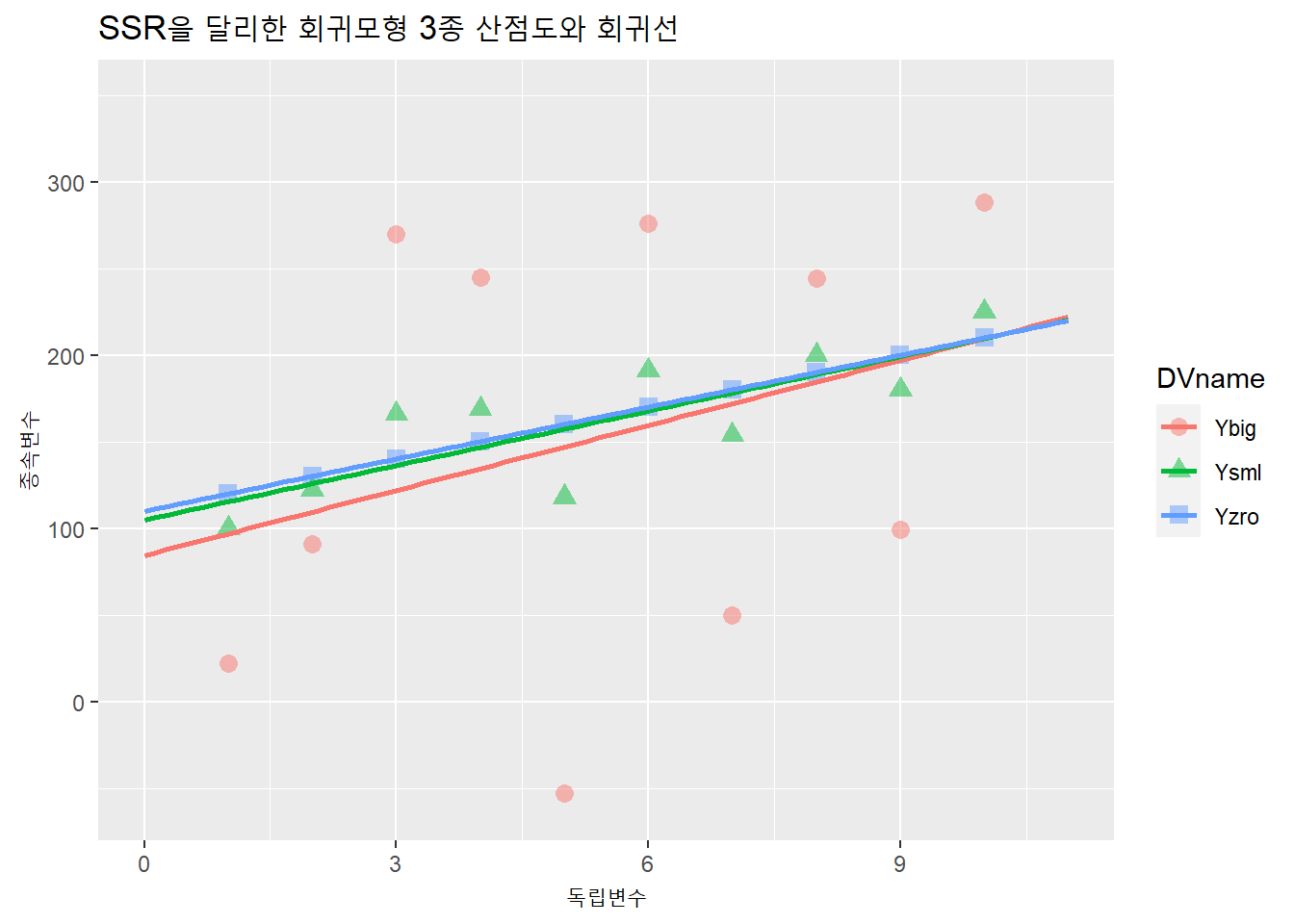
4.2 탐색적 회귀분석
탐색단계에서 회귀분석을 여러번 해봐야 할때가 있다. 독립변수가 6개라면 단순회귀분석을 6번 수행해야 한다. 가장 간단한 방법은 아래와 같이 lm()회귀식을 6번 쓰는 것이다.
lm(y ~ x1, df)
lm(y ~ x2, df)
lm(y ~ x3, df)
lm(y ~ x4, df)
lm(y ~ x5, df)
lm(y ~ x6, df)예를 들어, R내장데이터셋인 attitude를 회귀분석한다고 하자. 대형금융기관 30개 부서의 직원들이 관리자에 대해 평가한 자료다.
- 종속변수
- rating: 관리자의 업무수행에 대한 전반적인 평가
- rating: 관리자의 업무수행에 대한 전반적인 평가
- 독립변수
- complaints: 직원불평 처리 점수
- privileges: 특권 비허용도
- learning: 학습기회제공
- raises: 성과기반 승진
- critical: 저조한 성과에 질책
- advance: 직원의 승진 정도
- complaints: 직원불평 처리 점수
먼저 분석할 자료(attitude)를 살펴보자.
attitude %>% str()## 'data.frame': 30 obs. of 7 variables:
## $ rating : num 43 63 71 61 81 43 58 71 72 67 ...
## $ complaints: num 51 64 70 63 78 55 67 75 82 61 ...
## $ privileges: num 30 51 68 45 56 49 42 50 72 45 ...
## $ learning : num 39 54 69 47 66 44 56 55 67 47 ...
## $ raises : num 61 63 76 54 71 54 66 70 71 62 ...
## $ critical : num 92 73 86 84 83 49 68 66 83 80 ...
## $ advance : num 45 47 48 35 47 34 35 41 31 41 ...attitude %>% skim()| Name | Piped data |
| Number of rows | 30 |
| Number of columns | 7 |
| _______________________ | |
| Column type frequency: | |
| numeric | 7 |
| ________________________ | |
| Group variables | None |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| rating | 0 | 1 | 64.63 | 12.17 | 40 | 58.75 | 65.5 | 71.75 | 85 | ▃▃▇▅▅ |
| complaints | 0 | 1 | 66.60 | 13.31 | 37 | 58.50 | 65.0 | 77.00 | 90 | ▂▅▇▆▅ |
| privileges | 0 | 1 | 53.13 | 12.24 | 30 | 45.00 | 51.5 | 62.50 | 83 | ▂▇▅▅▁ |
| learning | 0 | 1 | 56.37 | 11.74 | 34 | 47.00 | 56.5 | 66.75 | 75 | ▃▇▇▃▇ |
| raises | 0 | 1 | 64.63 | 10.40 | 43 | 58.25 | 63.5 | 71.00 | 88 | ▂▇▇▆▂ |
| critical | 0 | 1 | 74.77 | 9.89 | 49 | 69.25 | 77.5 | 80.00 | 92 | ▂▂▂▇▂ |
| advance | 0 | 1 | 42.93 | 10.29 | 25 | 35.00 | 41.0 | 47.75 | 72 | ▅▇▆▂▂ |
attitude %>% describe()## vars n mean sd median trimmed mad min max range skew
## rating 1 30 64.63 12.17 65.5 65.21 10.38 40 85 45 -0.36
## complaints 2 30 66.60 13.31 65.0 67.08 14.83 37 90 53 -0.22
## privileges 3 30 53.13 12.24 51.5 52.75 10.38 30 83 53 0.38
## learning 4 30 56.37 11.74 56.5 56.58 14.83 34 75 41 -0.05
## raises 5 30 64.63 10.40 63.5 64.50 11.12 43 88 45 0.20
## critical 6 30 74.77 9.89 77.5 75.83 7.41 49 92 43 -0.87
## advance 7 30 42.93 10.29 41.0 41.83 8.90 25 72 47 0.85
## kurtosis se
## rating -0.77 2.22
## complaints -0.68 2.43
## privileges -0.41 2.23
## learning -1.22 2.14
## raises -0.60 1.90
## critical 0.17 1.81
## advance 0.47 1.8830행 7열의 데이터프레임이다. 모든 열은 숫자형이다. 모든 열에 결측값도 없다.
모든 변수 사이의 상관관계를 보자. (시각적 편의를 위해 4개 열만 선택했다.)
attitude %>% ggpairs(columns = 1:4)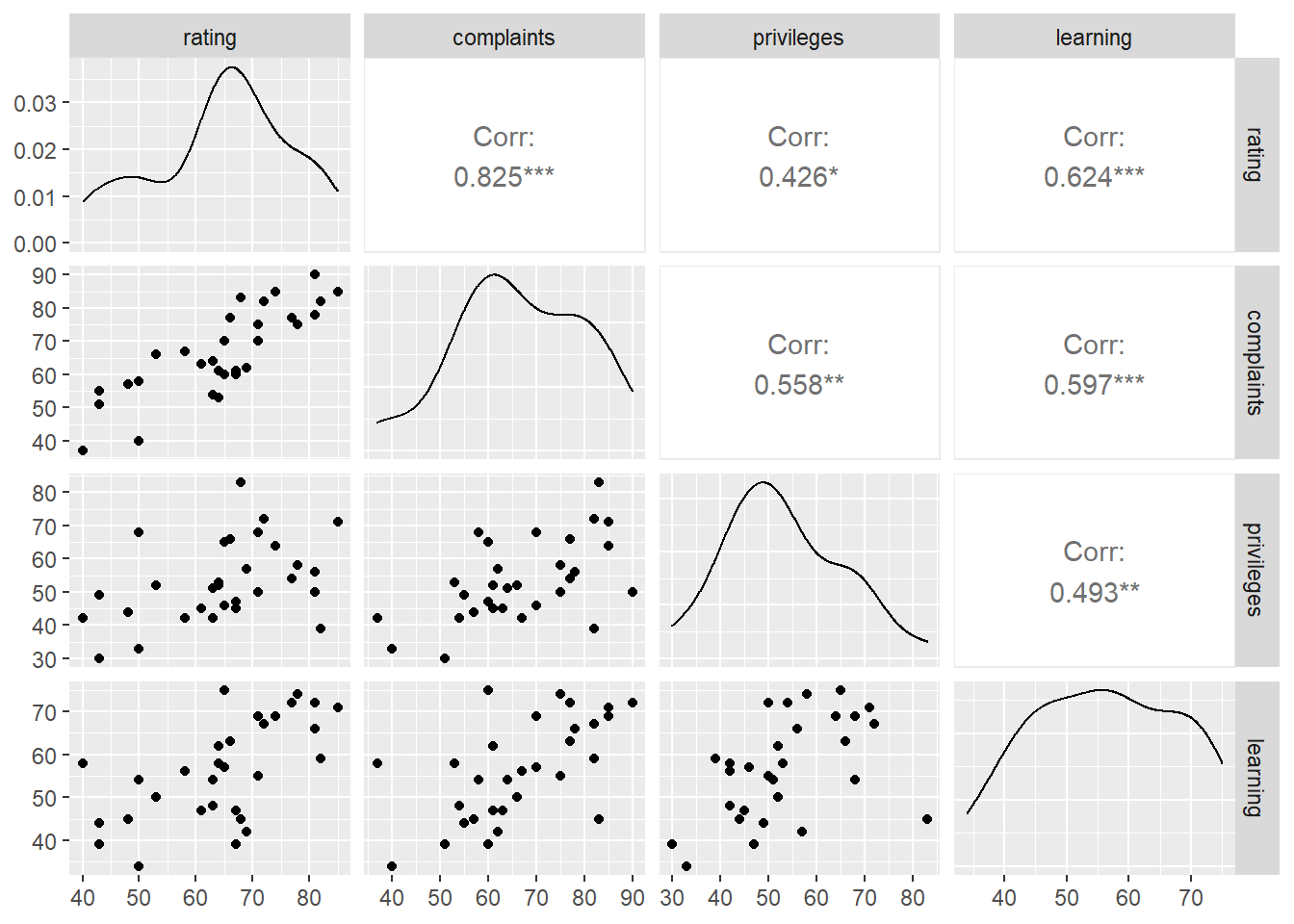
ggpairs()의 산점도에서 회귀선을 표현해보자.GGally패키지 ggpairs()함수의 lower =인자를 smooth로 지정한다. geom_smooth()의 기본값을 갖고 온다.
attitude %>%
ggpairs(columns = 1:4,
lower = list(continuous = "smooth"))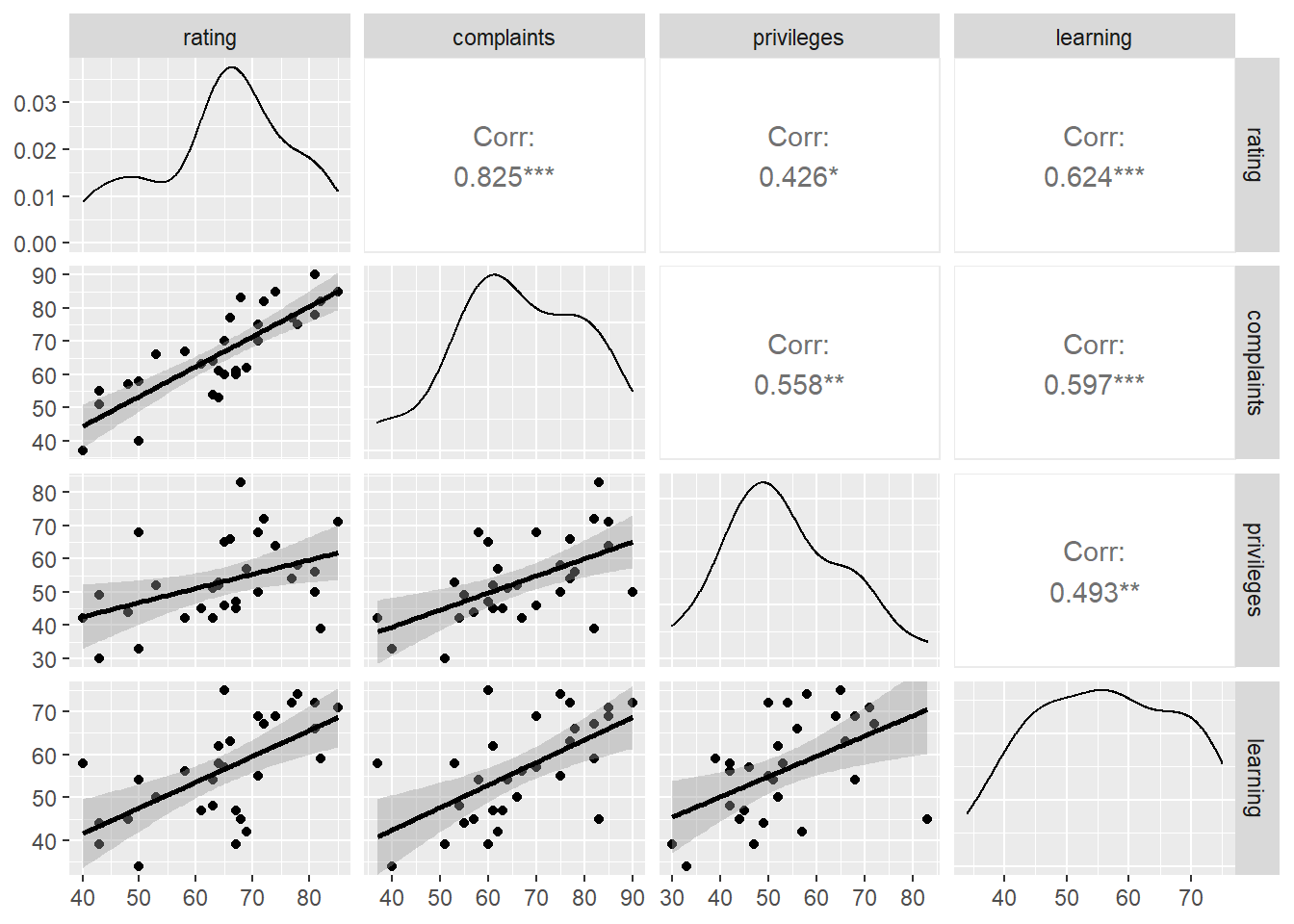
“complaints,” “privileges,” “learning,” “raises” 는 “rating”과 양의 상관성이 큰 편이고, “critical”과 “advance”매우 낮은 상관성이 보인다.
사용자함수를 만들어 산점도와 회귀선을 지정할 수 있다.
lm_f <- function(data, mapping, ...){
p <- ggplot(data = data, mapping = mapping) +
geom_point(alpha = .4, ...) +
geom_smooth(method = lm, color = "red", se = F, ...)
p
}
attitude %>%
ggpairs(columns = 1:4,
lower = list(continuous = lm_f))## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'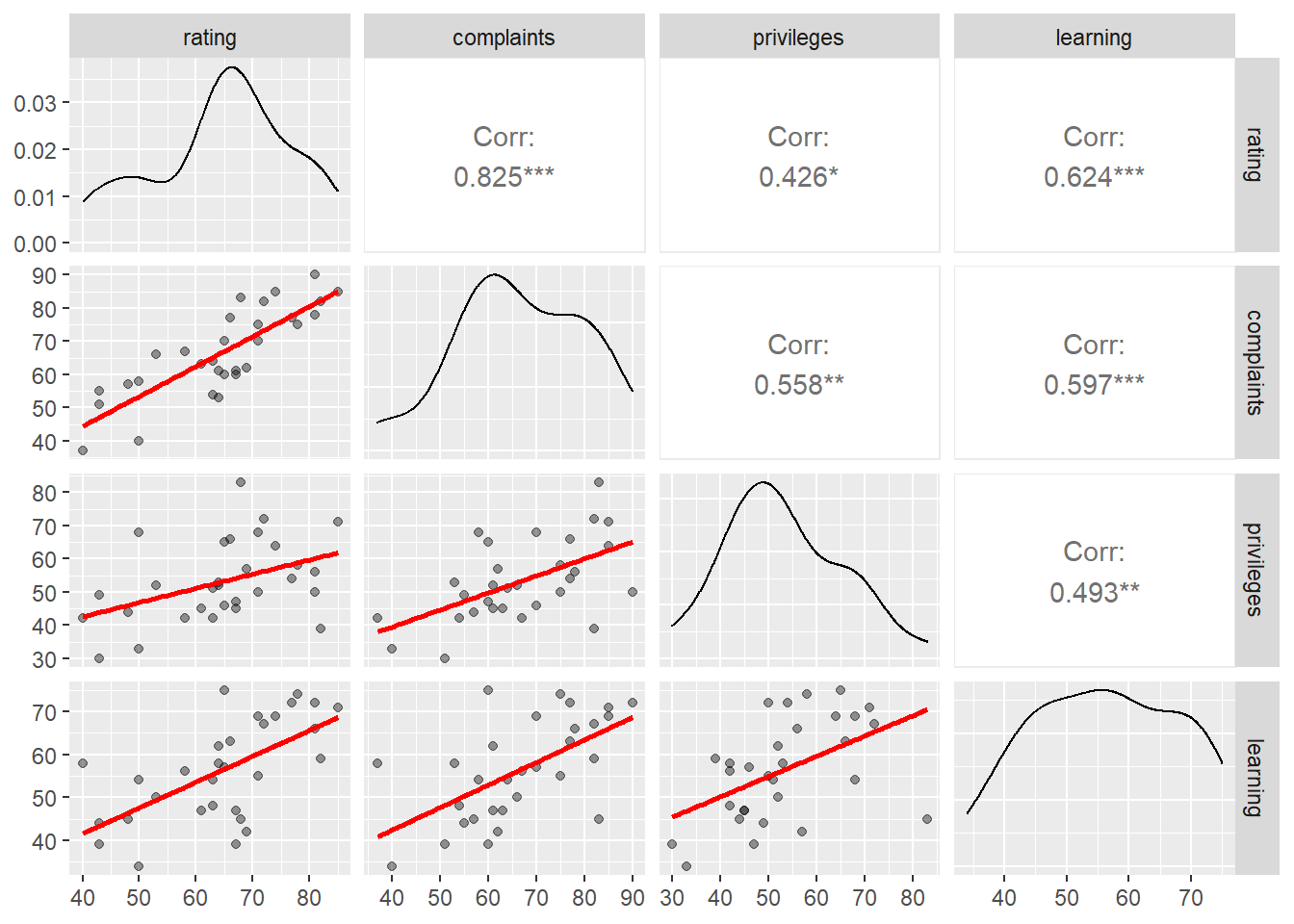
이제 각 독립변수를 종속변수에 대해 회귀분석을 해 기울기(\(\beta\))와 결정계수(\(R^2\))를 구해보자. 독립변수 6개의 종속변수에 대한 절편, 기울기, 결정계수 등의 계수를 추출하기 위해서는 아래와 같이 회귀분석을 여러번 반복해야 한다.
attitude %>%
lm(rating ~ complaints, .) %>% tidy() %>% .[,2]
attitude %>%
lm(rating ~ privileges, .) %>% tidy() %>% .[,2]
attitude %>%
lm(rating ~ learning, .) %>% tidy() %>% .[,2]
attitude %>%
lm(rating ~ raises, .) %>% tidy() %>% .[,2]
attitude %>%
lm(rating ~ critical, .) %>% tidy() %>% .[,2]
attitude %>%
lm(rating ~ advance, .) %>% tidy() %>% .[,2]
# 결정계수를 데이터프레임으로 부분선택.
attitude %>%
lm(rating ~ complaints, .) %>% glance() %>% .[,1]
attitude %>%
lm(rating ~ privileges, .) %>% glance() %>% .[,1]
attitude %>%
lm(rating ~ learning, .) %>% glance() %>% .[,1]
attitude %>%
lm(rating ~ raises, .) %>% glance() %>% .[,1]
attitude %>%
lm(rating ~ critical, .) %>% glance() %>% .[,1]
attitude %>%
lm(rating ~ advance, .) %>% glance() %>% .[,1]반복문을 이용해 한번에 계산하자. 이번엔 종속변수는 고정이고, 독립변수를 번갈아 투입한다. 독립변수가 바뀌면서 회귀모형을 구성하기 때문에, 결정계수를 회귀계수의 오른쪽에 배치하고, 각 회귀분석 결과표를 상하로 결합한다.
df <- attitude
names(df)## [1] "rating" "complaints" "privileges" "learning" "raises"
## [6] "critical" "advance"iv <- names(df)[-1]
dv <- names(df)[1]
output <- data.frame()
for(i in seq_along(iv)){
fml <- paste(dv, "~", iv[i]) # 회귀식
bt <- lm(fml, df) %>%
tidy() %>% .[,1:3] # 변수명, 회귀계수 표준오차
rs <- lm(fml, df) %>%
glance() %>% .[,1] # 결정계수
op <- bind_cols(bt, rs) # 좌우 열결합
output <- bind_rows(output, op) # 상하 행결합
}
output %>% gt() %>%
tab_header("rating에 대한 각 독립변수의 기울기와 결정계수") %>%
fmt_number(columns = -term, decimals = 2)| rating에 대한 각 독립변수의 기울기와 결정계수 | |||
|---|---|---|---|
| term | estimate | std.error | r.squared |
| (Intercept) | 14.38 | 6.62 | 0.68 |
| complaints | 0.75 | 0.10 | 0.68 |
| (Intercept) | 42.11 | 9.27 | 0.18 |
| privileges | 0.42 | 0.17 | 0.18 |
| (Intercept) | 28.17 | 8.81 | 0.39 |
| learning | 0.65 | 0.15 | 0.39 |
| (Intercept) | 19.98 | 11.69 | 0.35 |
| raises | 0.69 | 0.18 | 0.35 |
| (Intercept) | 50.24 | 17.31 | 0.02 |
| critical | 0.19 | 0.23 | 0.02 |
| (Intercept) | 56.76 | 9.74 | 0.02 |
| advance | 0.18 | 0.22 | 0.02 |
결정계수가 두번씩 나오므로, 이를 한번만 나오게 바꾸자. 없는 행(두번째 행)을 부분선택하도록해 결측값(NA)이 포함된 행을 만든다음, 결즉값을 “-”으로 바꾼다.
df <- attitude
iv <- names(df)[-1]
dv <- names(df)[1]
output <- data.frame()
for(i in seq_along(iv)){
fml <- paste(dv, "~", iv[i])
bt <- lm(fml, df) %>%
tidy() %>% .[,1:3]
rs <- lm(fml, df) %>% glance() %>%
.[1:2, 1] %>% # 없는 행 부분선택해 NA행 생성
arrange.(!is.na(r.squared)) # NA아닌값 위로 정열
op <- bind_cols.(bt, rs)
output <- bind_rows.(output, op)
}
output %>% gt() %>%
tab_header("rating에 대한 각 독립변수의 기울기와 결정계수") %>%
fmt_number(columns = -1, decimals = 2) %>%
fmt_missing(columns = -1) %>% # NA값을 -로 변경
cols_label(
estimate = md("_B_"), # 제목에 마크다운 문법 적용
std.error = md("_SE_"),
r.squared = html("<em>R<sup>2</sup></em>") # 제목에 html적용
)| rating에 대한 각 독립변수의 기울기와 결정계수 | |||
|---|---|---|---|
| term | B | SE | R2 |
| (Intercept) | 14.38 | 6.62 | — |
| complaints | 0.75 | 0.10 | 0.68 |
| (Intercept) | 42.11 | 9.27 | — |
| privileges | 0.42 | 0.17 | 0.18 |
| (Intercept) | 28.17 | 8.81 | — |
| learning | 0.65 | 0.15 | 0.39 |
| (Intercept) | 19.98 | 11.69 | — |
| raises | 0.69 | 0.18 | 0.35 |
| (Intercept) | 50.24 | 17.31 | — |
| critical | 0.19 | 0.23 | 0.02 |
| (Intercept) | 56.76 | 9.74 | — |
| advance | 0.18 | 0.22 | 0.02 |
4.2.1 계수의 해석
4.2.1.1 회귀계수
attitude 분석 결과에서 complaints의 rating에 대한 회귀모형은 다음과 같다.
\[rating = 14.38 + 0.75*complaints\]
직원불평처리점수가 1단위 올라갈때마다 관리자 평가점수가 0.75점 상승한다. 다른 독립변수에 대해서도 같은 방식으로 계산할 수 있다.
절편이 14.38이므로 직원불평처리점수를 0점 받으면 평가점수가 14.38이 된다. 그러나, 이 절편의 값은 실질적인 의미는 거의 없다. 독립변수를 절대 0점이 없는 등간척도로 측정했기 때문이다.
주의
회귀모형으로 독립변수가 종속변수를 설명하는 정도를 나타낼 수 있지만, 회귀분석을 통해 나타난 연관성이 반드시 인과성을 의미하지 않는다. 인과관계를 추론하기 위해서는 연관성 외에 시간적 선후 관계 및 제3변수(허위변수) 배제 등의 조건을 추가로 충족해야 한다.
4.2.1.2 표준화 회귀계수
attitude자료에는 독립변수가 여럿 있다. 한 독립변수의 기울기가 다른 독립변수의 기울기보다 크다고 반드시 큰 기울기가 실질적으로 큰 것은 아니다. 기울기를 비교하기 위해서는 표준화해서 비교해야 한다. 표준화 기울기(standardized beta)는 lm.beta패키지의 lm.beta()함수로 계산한다.
attitude %>% lm(rating ~ complaints, .) %>%
lm.beta() %>% coef()## (Intercept) complaints
## 0.0000000 0.8254176표준화했으므로 절편이 0이 된다. 기울기 계수도 조금 바뀐다. 다른 독립변수의 표준화 기울기와 비표준화기울기를 비교해보자. 기울기를 비표준화 계수와 표준화 계수로 구분할 때 표준화 기울기는 (\(\beta\))로 표기하고, 비표준화기울기는 (\(B\))로 표기한다.
df <- attitude
iv <- names(df)[-1]
dv <- names(df)[1]
output <- data.frame()
for(i in seq_along(iv)){
fml <- paste(dv, "~", iv[i])
bt <- lm(fml, df) %>%
tidy() %>% .[,1:3] # 변수명, 회귀계수, 표준오차
bts <- lm(fml, df) %>% lm.beta() %>%
tidy() %>% .[,2] # 표준화회귀계수
rs <- lm(fml, df) %>%
glance() %>% .[1:2, 1] %>% # NA행 추가
arrange.(!is.na(r.squared))
op <- bind_cols.(bt, bts, rs)
output <- bind_rows.(output, op)
}## New names:
## * estimate -> estimate...2
## * estimate -> estimate...4
## New names:
## * estimate -> estimate...2
## * estimate -> estimate...4
## New names:
## * estimate -> estimate...2
## * estimate -> estimate...4
## New names:
## * estimate -> estimate...2
## * estimate -> estimate...4
## New names:
## * estimate -> estimate...2
## * estimate -> estimate...4
## New names:
## * estimate -> estimate...2
## * estimate -> estimate...4output %>% gt() %>%
tab_header("rating에 대한 각 독립변수의 회귀계수와 결정계수") %>%
fmt_number(columns = -1, decimals = 2) %>%
fmt_missing(columns = -1) %>%
cols_label( # 열의 제목 지정
term = "Variable",
estimate...2 = md("_B_"), # 제목에 마크다운 문법 적용
std.error = md("_SE_"),
estimate...4 = html("β"), # 제목에 html문법 적용
r.squared = html("<em>R<sup>2</sup></em>")
)| rating에 대한 각 독립변수의 회귀계수와 결정계수 | ||||
|---|---|---|---|---|
| Variable | B | SE | β | R2 |
| (Intercept) | 14.38 | 6.62 | 14.38 | — |
| complaints | 0.75 | 0.10 | 0.75 | 0.68 |
| (Intercept) | 42.11 | 9.27 | 42.11 | — |
| privileges | 0.42 | 0.17 | 0.42 | 0.18 |
| (Intercept) | 28.17 | 8.81 | 28.17 | — |
| learning | 0.65 | 0.15 | 0.65 | 0.39 |
| (Intercept) | 19.98 | 11.69 | 19.98 | — |
| raises | 0.69 | 0.18 | 0.69 | 0.35 |
| (Intercept) | 50.24 | 17.31 | 50.24 | — |
| critical | 0.19 | 0.23 | 0.19 | 0.02 |
| (Intercept) | 56.76 | 9.74 | 56.76 | — |
| advance | 0.18 | 0.22 | 0.18 | 0.02 |
gt패키지의 cols_label()함수에서 열의 이름을 지정할 수 있다. 제목글자의 형식에는 md()함수로 마크다운 문법을 적용할수 있다. html()함수로는 html문법을 적용할 수 있다.
html태그 정보는 w3school에 잘 정리돼 있다.
4.3 다중회귀모형
복수의 독립변수를 독립변수의 수만큼 회귀분석을 하면 회귀선을 여러개 산출하므로 종속변수에 대해 하나의 예측값을 구할 수 없다. 복수의 독립변수로 하나의 예측값을 구하기 위해서는 복수의 독립변수를 동시에 투입하는 다중회귀모형(multiple regression model)을 이용한다.
다중회귀모형은 다음의 공식으로 나타낼수 있다.
\[Y = \alpha + \beta_1{X}_1 + \beta_2{X}_2 + ... + \beta_k{X}_k + \epsilon\]
- \(Y\): 종속변수(결과변수 or 반응변수)
- \(X_i\): \(i\)번째 독립변수(예측변수 or 설명변수)
- \(\alpha\): 절편(intercept)
- \(k\): 독립변수의 수
- \(\beta_i\): \(i\)번째 독립변수 \({X}_i\)의 회귀계수
- \(\epsilon\): 오차항(error).
복수의 독립변수가 있는 다중회귀분석에서도 \(\beta_i\)의 해석은 단순회귀모형과 본질적으로 같다. \(i\)번째 독립변수 \(X_i\)와 종속변수 \(Y\) 사이 연관성 정도다. 다만, “다른 모든 조건이 동일하다면 (cetaris paribus)”이라는 조건이 붙는다. 즉, 다른 독립변수가 고정됐을때(혹은 일정하게 유지됐을때) \(X_i\)가 한 단위 증가할 때 \(Y\)에 영향을 미치는 평균효과( \(Y\)가 \(\beta_i\)만큼 증가 또는 감소하는 정도)다.
다중회귀모형에서 한 독립변수의 회귀계수의 의미는 다른 모든 조건이 동일하다면 (cetaris paribus), 즉, 다른 모든 독립변수가 일정하게 유지된다면, 한 독립변수의 변화에 따른 종속변수의 평균변화량이다.
lm()함수를 이용해 다중회귀분석을 수행하는 방법은, 예를 들어, 독립변수가 3개인 경우 다음과 같다.
lm(y ~ x1 + x2 + x3, data)attitude자료에서 독립변수를 3개 선택해 rating을 예측하는 다중회귀모형을 만들면 다음과 같다.
\[ \operatorname{rating} = \alpha + \beta_{1}(\operatorname{complaints}) + \beta_{2}(\operatorname{privileges}) + \beta_{3}(\operatorname{learning}) + \epsilon \]
세 독립변수를 동시에 투입해 회귀분석해보자.
attitude %>%
lm(rating ~ complaints + privileges + learning, .) -> fit_at
tidy(fit_at) ## # A tibble: 4 x 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 11.3 7.32 1.54 0.136
## 2 complaints 0.682 0.129 5.30 0.0000154
## 3 privileges -0.103 0.129 -0.799 0.432
## 4 learning 0.238 0.139 1.71 0.0997위 분석 결과에서 complaints, privileges, learning의 rating에 대한 회귀모형은 다음과 같다.
\[rating = 11.26 + 0.68*complaints + -0.1*privileges + 0.24*learning\]
4.3.1 변수의 통제
다중회귀모형에서 회귀계수의 의미는 “다른 독립변수가 고정됐을때(혹은 일정하게 유지됐을때) \(X_i\)가 한 단위 증가할 때 \(Y\)게 영향을 미치는 평균효과( \(Y\)가 \(\beta_i\)만큼 증가 또는 감소하는 정도)”라고 했다. 다른 변수를 고정(혹은 일정하게 유지)하는것을 “다른 변수를 통제한다”고 표현한다.
만일, 모든 독립변수의 종속변수에 대한 연관성이 합산적(additive)즉, 개별 독립변수들이 종속변수에 미치는 영향이 서로 독립적이라면, 독립변수를 개별적으로 투입해 구성한 단순회귀모형의 회귀계수와 동시에 투입해 구성한 다중회귀모형의 회귀계수 사이에 차이가 없다.
변수들 사이의 관계도를 그리면 다음과 같다. (ggforce패키지 함수를 이용했다).
ggplot() +
geom_circle(aes(x0 = c(1), y0 = c(1,3), r = 1)) +
annotate("text", x = 1, y = 1,
label = "독립변수1", size = 6) +
geom_link0(aes(x = 2, xend = 3, y = 3, yend = 2),
arrow = arrow(angle = 15),
color = "red") +
annotate("text", x = 1, y = 3,
label = "독립변수2", size = 6) +
geom_link0(aes(x = 2, xend = 3, y = 1, yend = 2),
arrow = arrow(angle = 15),
color = "red") +
geom_circle(aes(x0 = c(4), y0 = c(2), r = 1)) +
annotate("text", x = 4, y = 2,
label = "종속변수", size = 6) +
coord_fixed() +
labs(title = "종속변수에 미치는 영향이 독립적") +
theme_void()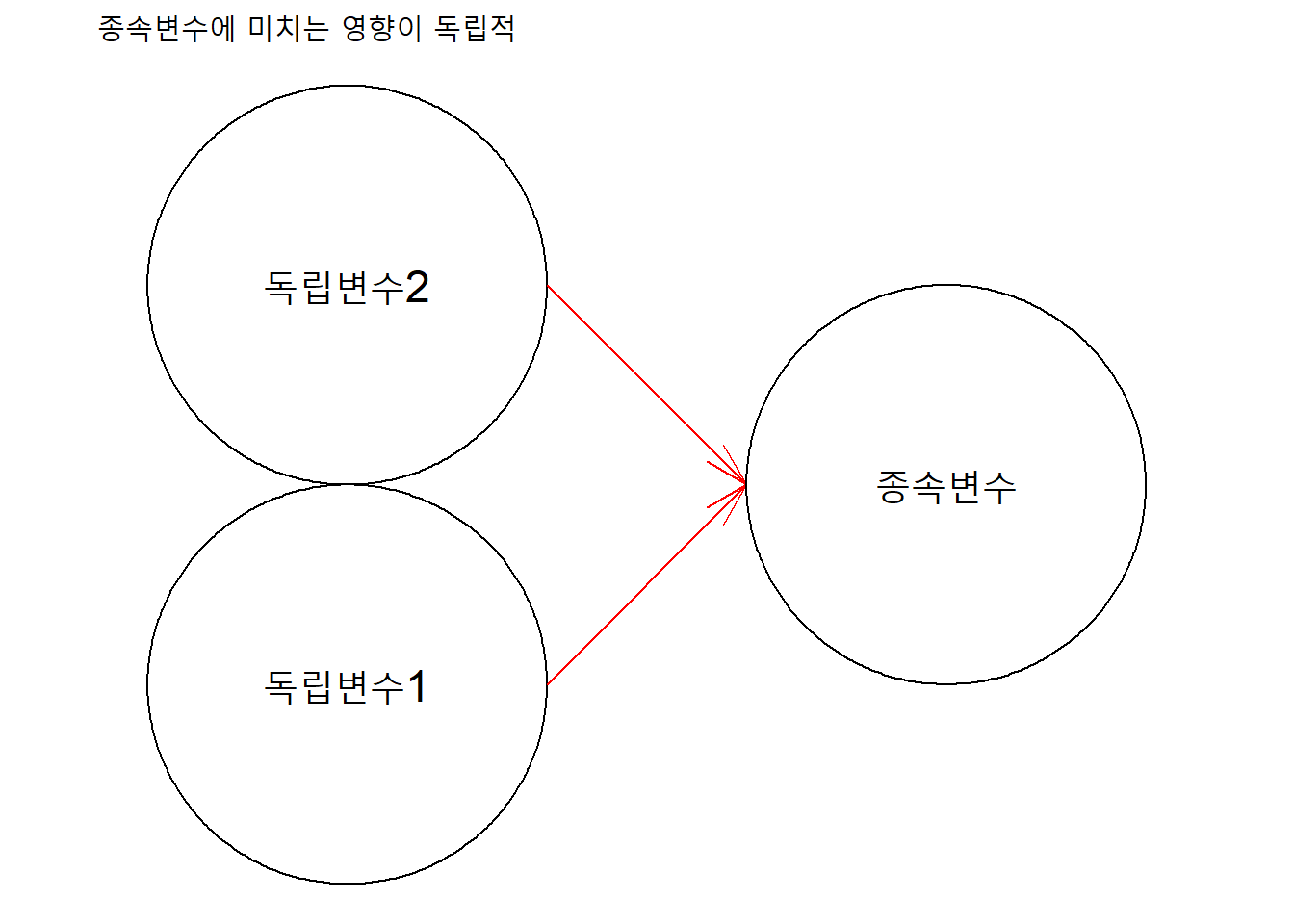
예를 들어, attitude자료에서 두 독립변수(complaints와 privileges)가 종속변수 rating에 미치는 효과가 서로 독립적이라면, complaints의 rating에 대한 효과에 대해 privileges가 영향을 미치지 않고, 그 반대 역시 마찬가지가 된다.
반면, 각 독립변수가 합산적이지 않아 서로 독립적이지 않다면, 한 독립변수가 다른 독립변수의 종속변수에 대한 효과에 대해 영향을 미친다.
ggplot() +
geom_circle(aes(x0 = c(1), y0 = c(1,2.5), r = 1)) +
annotate("text", x = 1, y = 1, size = 6,
label = "독립변수1") +
geom_link0(aes(x = 2, xend = 3, y = 1, yend = 1.75),
arrow = arrow(angle = 15),
color = "red") +
annotate("text", x = 1, y = 2.5, size = 6,
label = "독립변수2") +
geom_link0(aes(x = 2, xend = 3, y = 2.5, yend = 1.75),
arrow = arrow(angle = 15),
color = "red") +
geom_link0(aes(x = 2, xend = 2.5, y = 2.5, yend = 1.5),
arrow = arrow(angle = 15),
color = "red") +
geom_circle(aes(x0 = c(4), y0 = c(1.75), r = 1)) +
annotate("text", x = 4, y = 1.75, size = 6,
label = "종속변수") +
coord_fixed() +
labs(title = "종속변수에 미치는 영향이 비독립적") +
theme_void()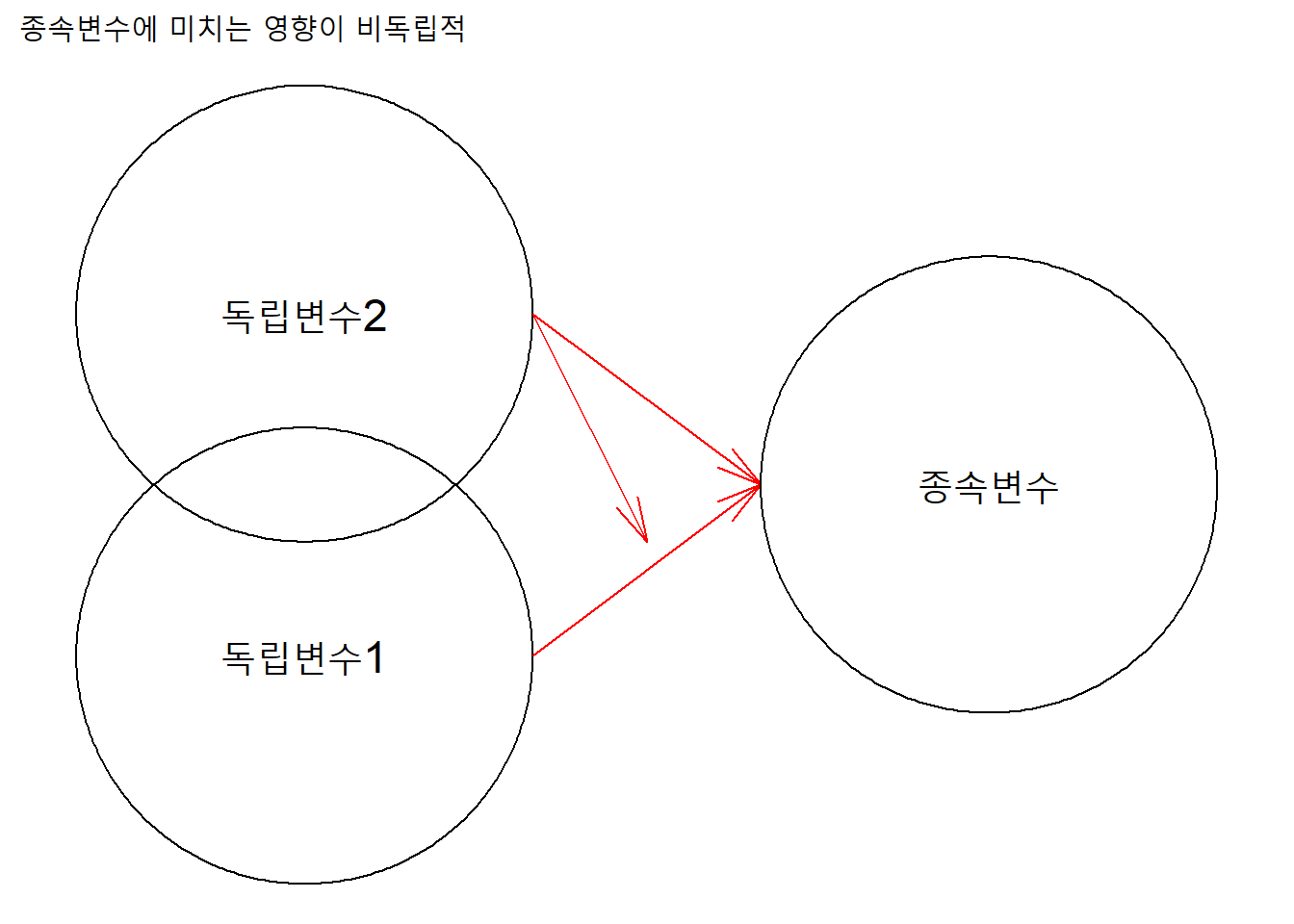
ggplot() +
geom_circle(aes(x0 = c(1), y0 = c(1,2.5), r = 1)) +
annotate("text", x = 1, y = 1, size = 6,
label = "독립변수1") +
geom_link0(aes(x = 2, xend = 3, y = 1, yend = 1.75),
arrow = arrow(angle = 15),
color = "red") +
geom_link0(aes(x = 2, xend = 2.5, y = 1, yend = 2),
arrow = arrow(angle = 15),
color = "red") +
annotate("text", x = 1, y = 2.5, size = 6,
label = "독립변수2") +
geom_link0(aes(x = 2, xend = 3, y = 2.5, yend = 1.75),
arrow = arrow(angle = 15),
color = "red") +
geom_circle(aes(x0 = c(4), y0 = c(1.75), r = 1)) +
annotate("text", x = 4, y = 1.75, size = 6,
label = "종속변수") +
coord_fixed() +
labs(title = "종속변수에 미치는 영향이 비독립적") +
theme_void()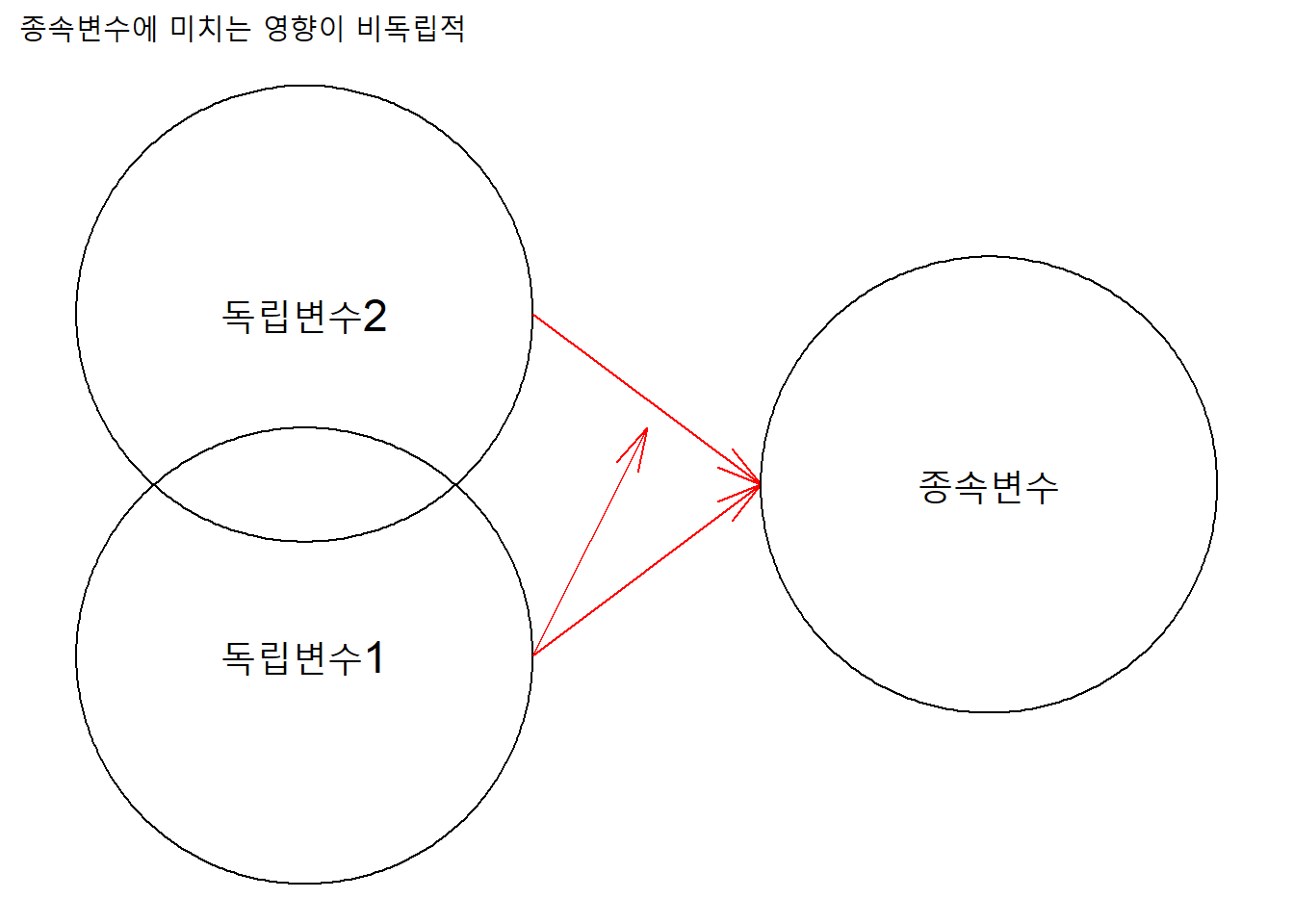
예를 들어, attitude자료에서 두 독립변수(complaints와 privileges)가 종속변수 rating에 미치는 효과가 서로 독립적이지 않다면, complaints의 rating에 대한 효과에 대해 privileges가 영향을 미치거나, 혹은 반대로 previliges의 rating에 대한 효과에 대해 complaints가 영향을 미칠수 있다. 회귀모형에서 종속변수의 변이를 설명하기 위해 투입한 변수를 독립변수라고 하고, 이 독립변수의 순효과를 파악하기 위해 투입한 다른 ’독립’변수는 통제변수(controlled variable)라고 한다.
complaints의 rating에 대한 효과를 파악하기 위해 회귀모형을 구성했다면, complaints를 독립변수라고 하고, previleges는 통제변수라고 부른다. 그 반대의 경우도 마찬가지다. 즉, 독립변수와 통제변수는 수학적인 기능은 동일하나, 통계적 의미는 다르다.
attitude자료에서 rating에 대한 privileges의 단순회귀모형과 complaints를 통제했을때의 다중회귀모형을 비교해보자.
# 오른쪽의 다중회귀모형 기준으로 열결합
right_join(
attitude %>%
lm(rating ~ privileges, .) %>%
tidy() %>% .[1:3, 1:3],
attitude %>%
lm(rating ~ privileges + complaints , .) %>%
tidy() %>% .[1:3, 1:3],
by = "term"
) %>%
gt() %>%
tab_header("단순회귀모형과 다중회귀모형의 회귀계수 비교") %>%
fmt_number(columns = -1, decimal = 2) %>%
fmt_missing(columns = -1) %>%
cols_label(
term = "독립변수",
estimate.x = md("_B_"),
std.error.x = md("_SE_"),
estimate.y = md("_B_"),
std.error.y = md("_SE_")
) %>%
tab_spanner(
label = "단순회귀모형",
columns = estimate.x:std.error.x) %>%
tab_spanner(
label = "다중회귀모형",
columns = estimate.y:std.error.y) | 단순회귀모형과 다중회귀모형의 회귀계수 비교 | ||||
|---|---|---|---|---|
| 독립변수 | 단순회귀모형 | 다중회귀모형 | ||
| B | SE | B | SE | |
| (Intercept) | 42.11 | 9.27 | 15.33 | 7.16 |
| privileges | 0.42 | 0.17 | −0.05 | 0.13 |
| complaints | — | — | 0.78 | 0.12 |
단순회귀모형에서 privilege의 회귀계수 0.42가 complaint를 함께 투여한 다중회귀모형에서는 -0.05가 됐다. complaints의 영향을 통제했을때, privileges가 1단위 증가할때 rating이 0.05단위 감소함을 나타낸다.
이 0.05단위의 변화를 독립변수의 변화에 따른 종속변수의 평균변화량을 나타내는 직접효과(direct effect) 혹은 순효과(net effect)라고 한다. 순효과라고 하는 이유는 다른 변수의 영향을 통제한 ‘순수한’ 효과이기 때문이다.
단순회귀모형에서 privileges 1단위 변화는 rating의 0.42만큼 설명했는데, complaints의 영향을 통제한 다중회귀모형에서는 -0.05만큼 설명한다. 이 -0.05가 다른 변수(complaints)의 영향을 통제한 priviledge의 rating에 대한 순효과다.
4.3.2 수정 결정계수
다중회귀모형은 단순회귀분석과 마찬가지로 모형적합도를 결정계수(\(R^2\))를 통해 나타낸다. 이에 더해, 수정된(adjusted) 결정계수(\(R^2_{adj}\))도 함께 계산한다. 수정된 결정계수는 자유도(degrees of freedom) 보정을 한 결정계수다. 자유도는 ‘자유롭게 변하는’ 관측수라고 할수 있는데, 보통 총 관측 수에서 추정할 계수의 수를 뺀 값으로 표시한다.
수정된 결정계수를 이용하는 이유는 독립변수를 회귀모형에 추가하면 잔차제곱합(SSR)이 감소하기 때문에 결정계수가 항상 증가하기 때문이다. 종속변수의 설명에 중요하지 않은 독립변수를 추가해도 결정계수가 증가하기 때문에 결정계수를 자유도 보정으로 하향조정한다.
위 모형에서 결정계수는 0.72이고, 수정된 결정계수는 0.68이다. 즉, 세 독립변수(complaints, privileges, learning)가 종속변수 rating을 약 68% 설명한다.
attitude %>%
lm(rating ~ complaints + privileges + learning, .) %>%
glance() %>% select.(r.squared, adj.r.squared) %>%
round(2) %>% gt() %>%
tab_header("complaints, priviledges, learning의 rating에 대한 회귀모형 적합도")| complaints, priviledges, learning의 rating에 대한 회귀모형 적합도 | |
|---|---|
| r.squared | adj.r.squared |
| 0.72 | 0.68 |
회귀분석결과 표에 결정계수를 포함해 구성하자. 변수2개(complaints와 priviledges)를 투입한 모형1과 변수 3개(complaints와 priviledges, learning)를 투입한 모형2를 비교하자. (사용자 함수를 만들어 구성한다.)
df <- attitude
names(df)## [1] "rating" "complaints" "privileges" "learning" "raises"
## [6] "critical" "advance"y <- 1
x1 <- c(2,3)
x2 <- c(2,3,4,5)
### 회귀분석결과 표 생성 사용자함수
reg_tbl <- function(df, y, x1, x2) {
## 변수 및 회귀모형
# 변수
dv <- names(df)[y]
iv_mdl1 <- names(df)[x1]
iv_mdl2 <- names(df)[x2]
# 모형1 회귀식
fml_mdl1 <- iv_mdl1 %>%
paste0(., collapse = " + ") %>%
paste0(dv, " ~ ", .)
# 모형2 회귀식
fml_mdl2 <- iv_mdl2 %>%
paste0(., collapse = " + ") %>%
paste0(dv, " ~ ", .)
# 표의 행 개수: 모형2 변수 + 절편행 개수
nn <- length(iv_mdl2) + 1
## 회귀분석 + 데이터프레임결합
model <- c(fml_mdl1, fml_mdl2)
output <- list()
for (i in seq_along(model)) {
df %>% lm(model[i], .) -> fit
# 변수명, 회귀계수, 표준오차 데이터프레임
op <- tidy(fit)[1:nn, 1:3] %>%
# 표준화 회귀계수 데이터프레임
bind_cols.(tidy(lm.beta(fit))[1:nn, 2]) %>%
# 결정계수 데이터프레임
bind_rows.(data.frame(
term = c("결정계수",
"수정결정계수"),
estimate...2 = c(summary(fit)$r.squared,
summary(fit)$adj.r.squared),
std.error = NA,
estimate...4 = NA
))
output <- list(output, op)
}
## 모형1과 모형2 결과 열결합해 표로 정리
output[[1]][[2]] %>%
bind_cols.(output[[2]]) %>%
select.(term = term...5, # 모형2 변수명
estimate...2:estimate...8) %>%
gt() %>%
tab_header(str_glue("{dv}에 대한 회귀분석결과")) %>%
fmt_number(-1, decimals = 2) %>%
fmt_missing(columns = -1) %>%
cols_label(
term = md("IV"),
estimate...2 = md("_B_"),
std.error...3 = md("_SE_"),
estimate...4 = html("β"),
estimate...6 = md("_B_"),
std.error...7 = md("_SE_"),
estimate...8 = html("β"),
) %>%
tab_spanner(
label = "Model 1",
columns = estimate...2:estimate...4) %>%
tab_spanner(
label = "Model 2",
columns = estimate...6:estimate...8) %>%
text_transform(
locations =
cells_body(
columns = term,
rows = term == "결정계수"),
fn = function(x) {
html(" - <em>R<sup>2</sup></em>")
}) %>%
text_transform(
locations =
cells_body(
columns = term,
rows = term == "수정결정계수"),
fn = function(x) {
html(" - <em>R<sup>2</sup><sub>adj</sub></em>")
}) %>%
tab_footnote(
footnote = str_glue("N = {nrow(df)}"),
locations = cells_title()
)
}
reg_tbl(df, y, x1, x2)## New names:
## * estimate -> estimate...2
## * estimate -> estimate...4
## New names:
## * estimate -> estimate...2
## * estimate -> estimate...4## New names:
## * term -> term...1
## * std.error -> std.error...3
## * term -> term...5
## * estimate...2 -> estimate...6
## * std.error -> std.error...7
## * ...| rating에 대한 회귀분석결과1 | ||||||
|---|---|---|---|---|---|---|
| IV | Model 1 | Model 2 | ||||
| B | SE | β | B | SE | β | |
| (Intercept) | 15.33 | 7.16 | 15.33 | 11.83 | 8.54 | 11.83 |
| complaints | 0.78 | 0.12 | 0.78 | 0.69 | 0.15 | 0.69 |
| privileges | −0.05 | 0.13 | −0.05 | −0.10 | 0.13 | −0.10 |
| learning | — | — | — | 0.25 | 0.15 | 0.25 |
| raises | — | — | — | −0.03 | 0.18 | −0.03 |
| - R2 | 0.68 | — | — | 0.72 | — | — |
| - R2adj | 0.66 | — | — | 0.67 | — | — |
| 1 N = 30 | ||||||
rating에 대해 privileges를 단순회귀모형으로 분석하면, privileges가 1단위 증가할때마다 rating은 0.42단위 증가하며, priviliges는 rating의 18%(결정계수)를 설명한다. 반면, complaints를 통제변수로 투입해 다중회귀모형으로 분석하면, privileges 1단위 증가할때마다 rating은 0.05단위 감소하며, privileges는 통제변수와 함께 rating의 66%(수정결정계수)를 설명한다.
4.4 적용
세계행복보고서2021 자료를 이용해 사회지지와 행복의 관계에 대해 탐색해보자. 이를 위해 GDP를 통제한 사회지지의 행복에 대한 회귀모형(모형1)과 GDP를 통제한 사회지지, 자율성, 부패지각의 행복에 대한 회귀모형(모형2)를 비교해보자.
4.4.1 수집정제
url <- "https://raw.githubusercontent.com/dataminds/art/main/whr/DataForFigure2.1WHR2021C2.xls"
rio::import(url) %>%
select.(1, 3, 7, 8, 10, 12) -> df
c("나라", "행복", "GDP", "사회지지", "자율성", "부패지각") -> colnames(df)4.4.2 기술통계와 상관분석
bind_cols.(
# 기술통계 데이터프레임
df %>% describe() %>%
add_rownames("V") %>%
select.(V, mean, sd) %>%
filter.(!str_detect(V, "\\*$")), # *로 끝나는 행 제외
# 상관관계 데이터프레임
df %>% select.(-나라) %>%
cor() %>% as.data.frame()
) %>% gt() %>%
tab_header(str_glue(
"평균, 표준편차 및 상관관계(n = {nrow(df)})")) %>%
fmt_number(-1, decimals = 2)## Warning: `add_rownames()` was deprecated in dplyr 1.0.0.
## Please use `tibble::rownames_to_column()` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was generated.| 평균, 표준편차 및 상관관계(n = 149) | |||||||
|---|---|---|---|---|---|---|---|
| V | mean | sd | 행복 | GDP | 사회지지 | 자율성 | 부패지각 |
| 행복 | 5.53 | 1.07 | 1.00 | 0.79 | 0.76 | 0.61 | −0.42 |
| GDP | 9.43 | 1.16 | 0.79 | 1.00 | 0.79 | 0.43 | −0.34 |
| 사회지지 | 0.81 | 0.11 | 0.76 | 0.79 | 1.00 | 0.48 | −0.20 |
| 자율성 | 0.79 | 0.11 | 0.61 | 0.43 | 0.48 | 1.00 | −0.40 |
| 부패지각 | 0.73 | 0.18 | −0.42 | −0.34 | −0.20 | −0.40 | 1.00 |
4.4.3 회귀분석
모형1은 행복이 예측되는 변수이므로 종속변수이고, 사회지지가 독립변수이며, GDP는 통제변수다. 회귀모형은 다음과 같다.
\[ \operatorname{행복} = \alpha + \beta_{1}(\operatorname{GDP}) + \beta_{2}(\operatorname{사회지지}) + \epsilon \]
모형2는 행복이 예측되는 변수이므로 종속변수이고, 사회지지, 자율성 및 부패지각이 독립변수이며, GDP는 통제변수다. 회귀모형은 다음과 같다.
\[ \operatorname{행복} = \alpha + \beta_{1}(\operatorname{GDP}) + \beta_{2}(\operatorname{사회지지}) + \beta_{3}(\operatorname{자율성}) + \beta_{4}(\operatorname{부패지각}) + \epsilon \]
각 변수의 회귀계수와 회귀모형의 결정계수를 표로 정리하면 다음과 같다. 앞서 만든 사용자함수 reg_tbl() 이용
df %>% select(-나라) -> df # 숫자형 변수만 선택
names(df)## [1] "행복" "GDP" "사회지지" "자율성" "부패지각"# 종속변수
y <- 1
# 모형1 독립변수
x1 <- c(2,3)
# 모형2 독립변수
x2 <- c(2,3,4,5)
reg_tbl(df, y, x1, x2)## New names:
## * estimate -> estimate...2
## * estimate -> estimate...4
## New names:
## * estimate -> estimate...2
## * estimate -> estimate...4## New names:
## * term -> term...1
## * std.error -> std.error...3
## * term -> term...5
## * estimate...2 -> estimate...6
## * std.error -> std.error...7
## * ...| 행복에 대한 회귀분석결과1 | ||||||
|---|---|---|---|---|---|---|
| IV | Model 1 | Model 2 | ||||
| B | SE | β | B | SE | β | |
| (Intercept) | −1.64 | 0.42 | −1.64 | −1.56 | 0.58 | −1.56 |
| GDP | 0.47 | 0.07 | 0.47 | 0.39 | 0.07 | 0.39 |
| 사회지지 | 3.34 | 0.72 | 3.34 | 2.70 | 0.67 | 2.70 |
| 자율성 | — | — | — | 2.26 | 0.49 | 2.26 |
| 부패지각 | — | — | — | −0.74 | 0.29 | −0.74 |
| - R2 | 0.67 | — | — | 0.75 | — | — |
| - R2adj | 0.67 | — | — | 0.74 | — | — |
| 1 N = 149 | ||||||
행복에 대해 GDP를 통제하고 사회지지를 독립변수로 투입한 모형1의 회귀모형으로 분석하면, 사회지지가 1단위 증가할때마다 행복은 3.34단위 증가하며, 모형1은 행복의 67%를 설명한다. 반면, 자율성과 부패지각을 추가로 독립변수로 투입한 모형2에서 사회지지는 1단위 증가할때마다 행복은 2.70단위 증가하며, 자율성은 1단위 증가할때 행복은 2.26단위 증가하고, 부패지각은 1단위 증가할 때 행복은 0.74단위 감소한다. 모형2는 행복을 74%를 설명한다.
4.5 종합
4.5.1 통계
- 선형회귀모형
- 종속변수(결과변수, 반응변수)
- 독립변수(예측변수, 설명변수)
- 절편(intercept)
- 비표준화기울기
- 표준화기울기
- 오차항(error, epsilon)
- 잔차(residual) = 예측오차(predictd error)
- 표준오차(standard error)
- 회귀선
- 최소제곱법(least square)
- 잔차제곱합(SSR: Sum of Squared Residual)
- 총제곱합(TSS: Total Sum of Squares)
- 최소자승회귀분석(Least Squares Regression)
- 표준회귀분석(OLS: Ordinary Least Squares)
- 모형적합도(model fit)
- 결정계수(\(R^2\): coefficient of determination)
- 다중회귀모형
- 통제변수
- 다른 조건이 동일하다면(일정하게 유지된다면; cetaris peribus)
- 직접효과(순효과)
- 수정결정계수(\(R^2_{adj}\))
4.5.2 코딩
- 파이프
- df %>% lm(fomula, data = .)
- 과학적기수법
- broom
- tidy()
- glance()
- augment()
- string
- stringr
- str_glue()
- str_detect()
- str_replace()
- paste0()
- paste0(., collapse = "")
- dplyr
- select()
- filter()
- arrange()
- mutate()
- recode()
- pivot_longer()
- pivot_wider()
- bind_cols()
- bind_rows()
- inner_join()
- left_join()
- right_join()
- full_join()
- NA
- is.na()
- ggplot2
- GGally
- ggpairs(columns, lower = list())
- annotate()
- theme_void
- ggforce
- geom_circle()
- geom_link0()
- coord_fixed()
- gt
- gt()
- tab_header()
- tab_spanner()
- fmt_number()
- fmt_missing()
- cols_label()
- text_transform()
- tab_footnote()
- md()
- html()