6 인과추론

c(
  "rio", "tidyverse", "tidytable", "psych", "psychTools", 
  "skimr", "janitor", "tidymodels", "lm.beta", "mediation",
  "GGally", "ggforce", "mdthemes", "patchwork", "ggdag",
  "r2symbols", "equatiomatic", "gt" 
  ) -> pkg 
sapply(pkg, function(x){
  if(!require(x, ch = T)) install.packages(x, dependencies = T)
  library(x, ch = T)
})

6.1 실재와 모형

우리가 알고 있는 세상은 세상 그 자체(실재)가 아니라 우리 마음 속에 비친 그림자, 즉 실재에 대한 모형이다 (Figure 6.1).

Figure 6.1: 다양한 착시

모형은 실재를 온전하게 반영하지 않기 때문에 실재에 대한 모형은 실제적인 일치 여부와 일치에 대한 지각 여부에 따라 4종으로 구분할 수 있다.

1유형: 진양성(true positive)
- 실재하는 존재에 대해 실재한다고 지각하는 경우
2유형: 위양성(false positive)
- 실재하지 않는 존재에 대해 실재한다고 지각하는 경우
3유형: 위음성(false negative)
- 실재하는 존재에 대해 실재하지 않는다고 지각하는 경우
4유형: 진음성(true negative)
- 실재하지 않는 존재에 대해 실재하지 않는다고 지각하는 경우

data.table(
  구분 = c("지각 유", "지각 무"),
  `실재 유` = c('진양성', "위음성"),
  `실재 무` = c('위양성', "진음성")
) %>% gt() %>% 
  tab_header(title = "실재와 인식의 4 유형") %>% 
  tab_options(
    heading.title.font.size = "middle",
    table.width = pct(80),
    column_labels.font.weight = "bold",
  )

실재와 인식의 4 유형
구분	실재 유	실재 무
지각 유	진양성	위양성
지각 무	위음성	진음성

6.1.1 인식방법으로서의 과학

실재와 실재에 대한 지각이 반드시 일치하지 않는다면, 우리는 어떻게 실재에 대한 지각이 실재를 제대로 반영하는지 알수 있을까? 두가지 기준이 있다.

문제해결 여부. 모형을 통해 문제가 해결된다면, 그 모형은 실재를 제대로 반영할 가능성이 높다.
학문공동체의 합의다. 대다수 학자가 합의한 모형도 그렇지 않은 모형보다 실재를 제대로 반영할 가능성이 높다(안도현 2021).

학문공동체가 모형에 대해 합의 하는 과정은 복잡하다. 관찰, 설문, 실험 등의 방법을 통해 논문을 쓰고, 동료검토 학술지에 투고해 심사를 받아 게재한 다음, 그 연구가 동료학자들에 의해 인용되고, 유사한 연구가 누적된 다음, 이들 연구를 종합하는 과정을 거친다.

문제해결과 학문공동체 합의과정의 근저에는 인식방법으로서의 과학에 있다.

과학이란 용어는 통상적으로 ’학문’이란 의미로 쓰인다. 대학 편제에 나와 있는 인문과학대학의 인문과학은 ’인문계열의 학문’이란 의미다. 인식방법으로서의 과학은 통상적으로 쓰이는 ’학문으로서의 과학’과는 구분해야 한다.

우선, 인식의 방법은 체계성에 따라 체계적인 과학과 통속과학으로 구분할 수 있다.

통속과학(folk science): 순진한 과학(naive science)이라고도 한다. 일반적인 사람들이 복잡한 실재에 대해 피상적으로 이해하고 해석하는 인식의 방법이다. 직관적으로 떠오르는 논리를 동원하거나, 개인적으로 겪었던 경험에 의지하는 인식방법이다.

통속과학이 물리학에 적용되면 통속물리학, 생물학에 적용되면 통속생물학, 심리학에 적용되면 통속심리학, 경제학에 적용되면 통속경제학이 되는 등 모든 분야에 통속적인 접근이 있다. 통속과학과 체계과학의 영역은 학문 분야별로 존재하나 크게 사물영역과 사회영역으로 구분할 수 있다. 사물영역은 대체로 자연과학의 영역이고, 사회영역은 대체로 사회과학의 영역이다.

체계적인 과학: 체계적인 논리와 체계적인 경험을 통해 실재에 대해 인식하는 방법이다. 달리 표현하면 과학은 체계적인 연역과 체계적인 귀납을 통한 인식의 방법이다. 통속과학과 체계적인 과학의 차이는 인식방법의 체계성에 있다.

6.1.1.1 논리의 체계성

논리의 체계성은 원인과 결과의 관계를 모순없이 구성하는데에 있다. 독립변수와 종속변수 사이의 연관성을 통해 인과관계를 추론하기 위해서는 연관성에 감추어진 인과관계와의 모순적 요소(역인과관계 및 허위관계)를 배제할 수 있어야 한다.

역인과관계 가능성 배제: 독립변수가 종속변수보다 시간적으로 선행.
허위관계 가능성 배제: 제3변수(허위변수)의 작용 통제.

6.1.1.2 경험의 체계성

경험의 체계성은 타당하고도 신뢰성있는 방법으로 자료를 생성하고 분석해 정보를 생성함으로써 논리적으로 기대되는 관계에 대한 근거를 제시하는데에 있다.

예를 들어, 회귀모형으로 독립변수가 종속변수를 설명하는 정도를 계산할 수 있다하여 그 연관성이 반드시 인과성을 의미하지 않는다. 독립변수를 종속변수의 원인으로 판단하기 위해서는 독립변수의 사건으로 인해 실제로 발생한 결과와 독립변수의 사건이 발생하지 않은 반사실적(counterfactual) 결과를 추론해 비교해야 한다. 즉, 인과추론은 ’사실(fact)’과 ’반사실(counterfact)’을 비교해 원인과 결과의 관계를 추론하는 것이다. (’사실’은 실제로 발생하는 사건을 의미하고, ’반사실’은 실제로 발생하지 않은 사건이다.)

저그마을의 갑돌이의 상황으로 가보자. 갑돌이가 보양제 복용과 기력 사이의 인과관계를 추론하기 위해서는 사실(저그A의 보양제 복용)과 반사실(저그A의 보양제 미복용)로 인한 결과(기력 수준)를 비교해야 한다. 그런데 반사실은 측정할 수 없다. 저그A가 보양제를 복용했다면, 보양제를 복용하지 않은 반사실은 측정할 수 없기 때문이다. 그 역도 마찬가지다. 저그A가 보양제를 복용하지 않았다면, 보용제를 복용한 결과를 측정할 수 없다.

인과추론의 근본문제: 발생하지 않은 사실(반사실)의 결과를 측정할 수 없는 문제.

6.1.1.3 실험

인과추론의 근본문제를 해결하기 위해서는 사실과 반사실을 비교할 수 있는 인위적 환경이 필요하다. 실험은 보양제 복용이라는 처치(treatment) 또는 조작(manipulation)의 결과와 미복용(즉, 독립변수를 조작하지 않은)의 결과를 비교함으로써 사실과 반사실의 결과를 대조할 수 있는 인위적 환경의 조성이다.

실험연구(experimental research): 독립변수를 처치하여(또는 조작하여) 사실과 반사실의 결과(종속변수에 대한 효과)를 비교함으로써 인과관계를 추론하는 인과추론 방법.

실험연구의 가장 이상적인 방법은 무작위대조시험(RCT: Randomized Controlled Trial)이다. 처치집단과 대조집단을 구분해 실험참가자들을 무작위로 처치집단과 대조집단에 할당한 다음, 처치집단과 대조집단 사이의 차이를 비교한다.

6.1.1.3.1 대조(처치의 통제)

대조(비교)는 실험연구가 실험연구이게 하는 핵심요소로서 처치집단(treatment group)과 대조집단(control group)의 결과 비교하는 것이다.

처치집단(= 실험집단): 독립변수로 작용하는 요소를 처치한 집단
대조집단(= 통제집단): 독립변수로 작용하는 요소를 처치하지 않은 집단.

대조집단이 ’처치하지 않은 집단’이라 하여 대조집단에 대해 아무 것도 하지 않은 상태로 두면 안된다. 대조집단은 처치집단에 처치되는 요소만 제외하고 다른 요소는 모두 유사해야 하기 때문이다.

예를 들어, 폭력미디어의 폭력행위가 시청자의 공격성에 미치는 영향을 파악하려면, 처치집단의 참가자는 폭력행위가 담긴 미디어(자극물)를 이용하고 대조집단의 참가자는 폭력행위가 담기지 않은 미디어를 이용한 후, 두 집단 사이의 공격성 수준을 비교한다.

만일, 대조집단의 자극물로 평온한 자연다큐멘타리를 사용했는데, 처치집단의 공격성이 대조집단에 대해 높게 나타난 경우, 그 공격성이 폭력내용에 의한 것인지, 아니면 흥분수준의 차이 때문인지 판단할 수 있다. 이 경우 흥분 수준은 혼란변수(confounder)가 된다.

따라서 대조집단을 구성할 때 자극물은 처치집단 뿐 아니라 대조집단에 제공해야 하며, 처치집단과 대조집단의 자극물의 구성은 가능한 독립변수의 요인만 차이가 나도록 구성해야 한다.

대조집단은 처치집단에 처치한 요소만 통제해 대조집단을 구성한다. 무작위대조시험에서 대조에 해당하는 용어가 controlled(통제)이고, 대조집단을 통제집단이라고 하는 이유다.

6.1.1.3.2 무작위 할당

처치집단과 대조집단을 구성할때 처치를 제외한 모든 측면에서 유사하게 구성하지 않으면 제3변수의 작용 가능성을 온전하게 배제할수는 없다.

처치집단과 대조집단 사이의 유일한 체계적인 차이가 처치로 인한 결과의 차이가 돼야, 다른 잠재적 요인의 영향을 배제할 수 있어, 종속변수의 값을 독립변수에 의한 인과효과로 해석할 수있다.

만일 처치집단과 대조집단 사이에 체계적인 차이(예: 처치집단은 주로 남성, 대조집단은 주로 여성)가 존재한다면 처치집단과 대조집단의 차이가 처치에 따른 결과의 차이인지, 표본의 차이에 의한 결과인지 구분할 수 없다.

처치집단과 대조집단 사이의 체계적 차이를 오직 처치에 의한 차이로만 만들기 위해서는, 즉 처치요소를 제외하고 모든 요소를 유사하게 만들기 위해서는, 처치집단과 대조집단에 대해 측정대상(예: 연구참여자)을 무작위 할당하는 것이 이상적이다.

주요 변수(예: 성)를 지정해 균일하게 할당하는 것이 무작위할당보다 더 나은 방법이라고 판단할 수 있다. 그러나 결과에 미치는 영향이 성 이외 무슨 변수에 의한 것인지 알수 없기 때문에 무작위할당이 가장 이상적인 방법이다.

RCT의 장단점

장점

내적타당성(internal validity): 관측한 효과를 당초 관측하고자 한 효과로 추정할 수 있는 정도(인과추론의 가정이 충족되는 정도). 대조와 무작위할당을 통해 제3변수의 작용과 역인과가능성을 배제할 수 있다.

단점

외적타당성(external validity): 관측한 효과를 측정한 표본이외의 집단에도 적용할 수 있는 정도(결론을 일반화할 수 있는 정도). 실험상황은 인위적 환경이므로 현실의 상황과 반드시 일치하지 않는다.

자연적으로 발생하는 실험상황(자연실험)의 경우 실험연구의 외적타당성 한계를 극복할 수 있다.

관찰연구의 장단점

RCT를 통해 내적으로 타당한 인과효과를 추정할 수 있으나, 시간·공간· 비용 등의 한계 때문에 처치할당을 무작위로 하기 어려운 경우가 많다. 현실적인 이유로 측정 대상에 대해 인위적 조작(처치)을 하지 않는 관찰연구(observational study)를 선택하는 경우가 많다. 관찰연구는 RCT에 비해 내적타당도가 떨어지만, 인위적 개입을 최소화했기 때문에 외적타당도가 높은 장점이 있다.

장점

내적타당성: 관측한 효과를 당초 관측하고자 한 효과로 추정할 수 있는 정도가 낮다. 즉, 제3변수의작용 및 역인과가능성을 배제하기 어려워 인과추론의 가정이 충족되는 정도가 낮다.

단점

외적타당도: 자연환경에서 연구자의 개입을 최소화했으므로, 관측한 효과를 다른 표본에도 적용할 수 있는 정도, 즉 결론을 일반화할 수 있는 정도가 높다.

6.2 통계적 추정

과학은 논리와 경험을 이용한 인식의 방법이다. 논리를 통해 가설을 설정하고, 이 가설이 측정자료와 일치할때 실재에 대한 모형을 과학적으로 구성했다고 추정할 수 있다.

그렇다면 우리는 어떻게 가설이 측정자료와의 일치여부를 판단할수 있을까? 처치집단과 대조집단의 차이가 우연의 결과인지 혹은 처치의 효과 때문인지 여부를 어떻게 판단할 수 있을까? 그 판단의 오류 여부를 어떻게 가늠할 수 있을까?

이 문제를 해결하기 위해 가장 널리 사용되는 방법이 통계적 가설검정(Hypothesis test)이다. 통계적 가설검정은 표본의 측정결과를 모집단의 값으로 적용할 수 있는지 여부를 통계적으로 추정하는 방법이다.

6.2.1 모집단과 표본

우리는 실재의 모든 면을 측정할 수 없다. 오직 특정 부분만 측정가능하다. 실재를 모집단(population)이라고 한다면, 우리가 측정할 수 있는 대상은 모집단의 일부를 표집(sampling)한 표본(sample)이다. 즉, 우리는 표본을 통해 모집단의 실체를 추론한다. 따라서 실재와 모형의 불일치(인식의 오류) 여부는 표본이 모집단을 어느 정도로 정확하게 반영하는지에 달려 있다.

모집단(population): 인식하고자 하는 개인 혹은 개별관측대상의 집합 혹은 인식 대상 전체(즉, 알고 싶은 대상 전체). 예를 들어, 지구에 사는 모든 사람, 한국 국적의 모든 시민, 90년대에 태어난 모든 사람 등. 모집단의 수치에는 ’모’를 붙여 모수치(parameter)라고 한다. 모집단의 평균은 모평균(\(\mu\): mu), 모집단의 표준편차는 모표준편차(\(\sigma\): sigma), 모집단의 비율은 모비율(\(p\)).
표본(sample): 모집단의 일부. 표본의 수치는 통계치(statistic)라고 한다 (Statistics는 통계학). 표본의 평균은 표본평균(\(\overline{X}\): x bar), 표본의 표준편차는 표본표준편차(\(S\)), 표본의 비율은 표본비율(\(\widehat{p}\): p hat).

값	모수치 표기	통계치 표기
갯수	\(N\)	\(n\)
평균	\(\mu\)(mu)	\(\overline{x}\)(x bar) or \(\widehat{\mu}\)(mu hat)
표준편차	\(\sigma\)(sigma)	\(S\)
비율	\(p\)	\(\widehat{p}\)(p hat)

두 수의 비교: 비(ratio) vs. 비율(proportion)

비(ratio): 두 수를 비교하여 나타낸 것
- 비교하는 양 / 기준량
- 예: 남학생 12명, 여학생 18명인 경우 여학생(기준량)에 대한 남학생(비교하는 양)의 비(ratio)는 12/18 또는 12:18
비율(proportion): 기준량에 대한 비교하는 양의 크기
- 비교하는 양 / (비교하는양 + 기준량)
- 예: 남학생 12명, 여학생 18명인 경우 남학생(비교하는 양)의 비율(propotion)는 12/(12+18)
백분율: 기준량이 100인 비율

전수조사(census): 모집단의 모든 구성요소를 대상으로 한 조사. 모집단에 대해 시간과 공간을 특정(예: 2022년 1월에 재직중인 A회사 직원)하지 않는 이상, 전수조사(census)는 불가능하다. 모집단에는 현재 뿐 아니라 과거 및 미래에 존재할 대상들도 포함되기 때문이다. 예를 들어, ’A회사 직원’을 모집단이라고 한다면 과거에 직원이었던 사람과 미래에 직원일 사람이 모두 해당한다.

6.2.1.1 표집(sampling)

대부분의 경우 전수조사를 할수 없기 때문에, 모집단의 모수치를 직접 측정할수는 없고 대신 모집단의 개체를 표집(sampling)해 구성한 표본의 통계치를 통해 추정한다.

표집: 모집단에서 개체를 추출해 표본을 구성하는 행위.

표본 통계치로 모집단 모수치를 추정하기 위해서는 표본이 모집단을 대표(representative)할 수 있어야 하며, 표본에서 도출한 결과를 모집단에 일반화(generalizse)할 수 있어야 한다. 즉, 표본이 모집단과 ’비슷’해야 한다. 이를 위해서는 표집이 무작위(random)로 이뤄져야 한다.

또한 모집단에서 특정 개체를 추출한 행위가 다른 요소를 추출하는 확률에 영향을 주지 말아야 한다. 즉, 특정 구성요소를 추출했다고 해서 다른 구성요소가 추출될 확률을 높이거나 낮춰서는 안된다. 이를 독립성이라고 한다.

표집이 무작위적으로, 그리고 독립적으로 이뤄지게 되면 모집단의 각 개체가 표본으로 포함될 기회가 같아지는데, 이를 표본의 불편향성(unbiased)이라고 한다.

6.3 확률

확률(probability)은 ’발생 가능한 모든 경우의 수’에 대한 ’특정 사건이 발생할 수 있는 경우의 수’의 비율이다.

\[ \frac{사건A가 발생할 수 있는 경우의 수}{발생 가능한 모든 경우의 수} = P(A) \] 동전을 던지면 앞면이 나올 수도 있고 뒷면이 나올수도 있다. 공평한 동전이라면, 앞면이 나올 확률은 1/2이 된다.

\[ {동전 앞면이 발생할 수 있는 경우의 수 \over 동전 앞면과 뒷면이 발생할 모든 경우의 수} = {1 \over 2} \] 확률은 시행(trial), 표본공간(sample space), 사건(event)의 세가지 개념을 이용해 정의한다.

시행: 확률적인 사건을 만들어내는 일련의 작업. 동전 던지기, 주사위 던지기 등이다.
표본공간: 가능한 모든 시행결과의 집합. 예를 들어, 동전을 던지는 시행을 할 경우, 가능한 모든 시행 결과는 앞면(H)이 나오는 경우와 뒷면(T)이 나오는 경우가 있다. 따라서, 동전을 한번 던졌을 때의 표본공간은 {H, T}이 된다. 주사위를 한번 던지는 경우의 표본공간은 {1, 2, 3, 4, 5, 6}이다. 표본공간은 \(\Omega\)로 표시한다.
사건: 표본공간의 부분집합. 표본공간은 어떠한 부분집합도 포함하므로, 표본공간 전체도 사건이고 공집합도 사건이라고 할수 있다.

사건 A가 발생할 확률(\(P(A)\)은 다음과 같이 나타낼수 있다.

\[ P(A) = \frac{사건A집합 요소의 수}{표본공간(\Omega) 요소의 수} \]

앞면과 뒷면의 경우의 수 확률이 같은 공평한(fair) 동전을 두번 던지는 경우, \(\Omega\) = {HH, HT, TH, TT}로서 표본공간 요소의 수는 4가 된다. 앞면이 단 한번이라도 나오는 사건의 집합 요소는 3이다. \(A\) = {HH, HT, TH}. 따라서, 동전을 두번 던져 앞면(H)이 단 한번이라도 나올 확률\(P(A)\)은 \(3/4\)이 된다.

동전던지기는 sample()함수를 통해 가상으로 시행해볼수 있다.

sample(x, size, replace = FALSE, prob = NULL)

x: 표본공간(벡터)
size: 추출할 요소의 갯수()
replace: 추출한 요소복원 여부. 비복원이 기본값.
prob: 표본공간에서 특정 요소가 추출될 확률. 기본값은 NULL

표집의 방법에는 추출한 개체의 복원(replacement) 여부에 따라 복원추출(sampling with replacement)과 비복원추출(sampling without replacement)로 구분한다.

복원추출: 각 개체를 추출한 다음 개체를 다시 모집단에 돌려놓고 추출. 동일한 개체를 반복적으로 추출 가능.
비복원추출: 각 개체를 추출한 다음 모집단에 돌려놓지 않고 추출. 각 개체는 최대 한번까지만 추출.

불공평한 동전을 만들어, 앞면(H)의 경우의 수를 0.8, 뒷면(T)의 경우의 수를 0.2로 설정해 10회 복원추출해보자.

c("H", "T") %>% sample(size = 10, replace = T, prob = c(0.8, 0.2))

##  [1] "H" "H" "T" "H" "H" "H" "H" "T" "H" "H"

아래 코드는 Error in sample.int(length(x), size, replace, prob) : cannot take a sample larger than the population when 'replace = FALSE'('replace = FALSE' 일때는 모집단보다 큰 샘플을 가질 수 없습니다)로 오류가 발생한다. 비복원추출이므로 표본의 크기를 2개 이상 만들수 없기 때문이다.

# 비복원추출
c("H", "T") %>% sample(size = 10, replace = F)

비복원추출일때는 추출할 요소의 개수가 표본공간의 크기와 작거나 같아야 한다.

c("HH", "HT", "TH", "TT") %>% sample(size = 4, replace = F)

## [1] "TH" "TT" "HH" "HT"

prob =는 값을 지정하지 않으면 모든 경우의 수가 동일하게 지정된다.

c("H", "T") %>% sample(size = 10, replace = T)

##  [1] "T" "H" "T" "H" "T" "T" "H" "H" "T" "H"

그런데, 실제로 표집한 결과를 계산해보면 앞면과 뒷면 갯수가 각각 5개가 아니다.

set.seed(37)
c("H", "T") %>% sample(size = 10, replace = T) %>% 
  janitor::tabyl()

##  . n percent
##  H 4     0.4
##  T 6     0.6

앞면과 뒷면 경우의 수가 같으므로 수학적으로는 확률이 0.5이어야 하지만, 특정 사건이 발생할 통계적 확률은 반드시 수학적 확률과 일치하지는 않기 때문이다. 특정 사건이 발생활 확률과 수학적 확률 사이의 차이를 표집오차(sampling error)라고 한다.

시행횟수를 매우 많이 늘리면 통계적 확률은 수학적 확률에 근접해진다. 따라서 표집오차는 시행회수가 증가하면 감소한다.

set.seed(37)
c("H", "T") %>% sample(size = 10000, replace = T) %>% 
  janitor::tabyl()

##  .    n percent
##  H 4993  0.4993
##  T 5007  0.5007

6.3.0.1 확률변수

확률을 구하기 위해서는 각각의 사건에 특정 값이 할당돼야 한다. 각각의 사건에 값을 할당하는 것을 확률변수(random[stochastic] variable)라고 한다. 즉, 확률변수는 표본공간의 각 사건에 값을 할당하는 함수다.

예를 들어, 동전던지기를 한번 시행하는 경우 표본공간은 앞면(H)과 뒷면(T) 등 2개의 사건이 생기는데, 여기서 확률변수는 앞면과 뒷면이라는 각 사건에 값(예: H = 1, T = 0)을 할당하는 것이다. 이를 확률변수 \(X\)라고 한다면 다음과 같이 나타낼 수 있다.

\[ \begin{equation} X = \begin{cases} 1 : & if & H \\ 0 : & if & T \\ \end{cases} \end{equation} \] 동전던지기를 2회 시행하면 표본공간은 4개의 사건(HH, HT, TH, TT)이 생기고, 동전의 앞면(H)이 나오는 회수를 확률변수 \(Y\)라고 한다면 확률변수 \(Y\)의 값은 0, 1, 2가 된다.

\[ \begin{equation} Y = \begin{cases} 2 : & if & HH \\ 1 : & if & HT, TH \\ 0 : & if & TT \\ \end{cases} \end{equation} \]

확률변수는 취하는 값에 따라 이산확률변수(discrete random variable)와 연속확률변수(continuous random variable)로 구분한다.

이산확률변수: 범주형 값을 취하는 확률변수
- 예: 주사위 던지기(1, 2, 3, 4, 5, 6): 값과 값 사이에 값이 없다.

베르누이확률변수(Bernoulli random variable)

이산확률변수 중 동전던지기처럼 확률변수의 값이 앞면과 뒷변으로 2개의 고유한 값을 취하는 확률변수를 이진확률변수(binary radom variable) 또는 베르누이확률변수(Bernoulli random variable)라고 한다.

연속확률변수: 연속형 값을 취하는 확률변수형
- 예: 한국인의 키: 값과 값 사이에 셀수 없이 많은 값이 있다.
- A대학교 학생이 태어난 해: 연도는 자연수이므로 값과 값 사이에 값이 없지만, 연도는 무한하게 확장 가능하므로 연속형 값.

6.3.0.2 확률분포

동전던지기를 3회 시행했을 때 앞면(H)이 나오는 회수를 확률변수 \(X\)라고 하는 경우, 표본공간은 모두 8개의 사건으로 이뤄진다.

\[ HHH, HHT, HTH, HTT, THH, THT, TTH, TTT \]

확률변수 \(X\)의 값은 다음과 같다.

\[ \begin{equation} X = \begin{cases} 3 : & if & HHH \\ 2 : & if & HHT, HTH, THH \\ 1 : & if & HTT, THT, TTH \\ 0 : & if & TTT \\ \end{cases} \end{equation} \] 따라서 각 확률변수의 값에 대한 확률은 다음과 같다.

\[ P(X = 3) = \frac{1}{8} \\ P(X = 2) = \frac{3}{8} \\ P(X = 1) = \frac{3}{8} \\ P(X = 0) = \frac{1}{8} \\ \] 이처럼 확률이 각각의 확률변수의 값에 대해 흩어진 정도가 확률분포다. 예를 들어, 동전던지기 3회 시행해 앞면이 나올 확률은 {HHH}와 {TTT}에 각각 1/8씩 분포돼 있고, {HHT, HTH, THH}와 {HTT, THT, TTH}에 각각 3/8씩 분포돼 있다.

확률분포는 확률변수의 종류에 따라 이산확률분포(이항분포, 베르누이분포)와 연속확률분포로 나뉜다.

6.3.0.3 이산확률분포

베르누이 시행으로 생기는 확률변수의 값은 베르누이분포를 만들고, 베르누이 시행을 n번하는 이항시행(binomial trial)으로 생기는 확률변수의 값은 이항분포(binomial distribution)를 만든다.

이항시행을 3회 실시한 표본을 만들어 이항분포를 시각화해보자. 수학적확률과 근사한 값을 얻기 위해 표본의 갯수를 80000개로 크게 설정했다.

set.seed(73)
dist_br <- rbinom(n = 80000, size = 3, prob = .5) %>% factor()
data.table(x = dist_br)  %>% 
ggplot(aes(x)) + 
  geom_bar(width = .9, fill = "deeppink", alpha = .6) +
  labs(title = "이항분포",
       x = "확률변수의 값") +
  theme(title = element_text(size = 15))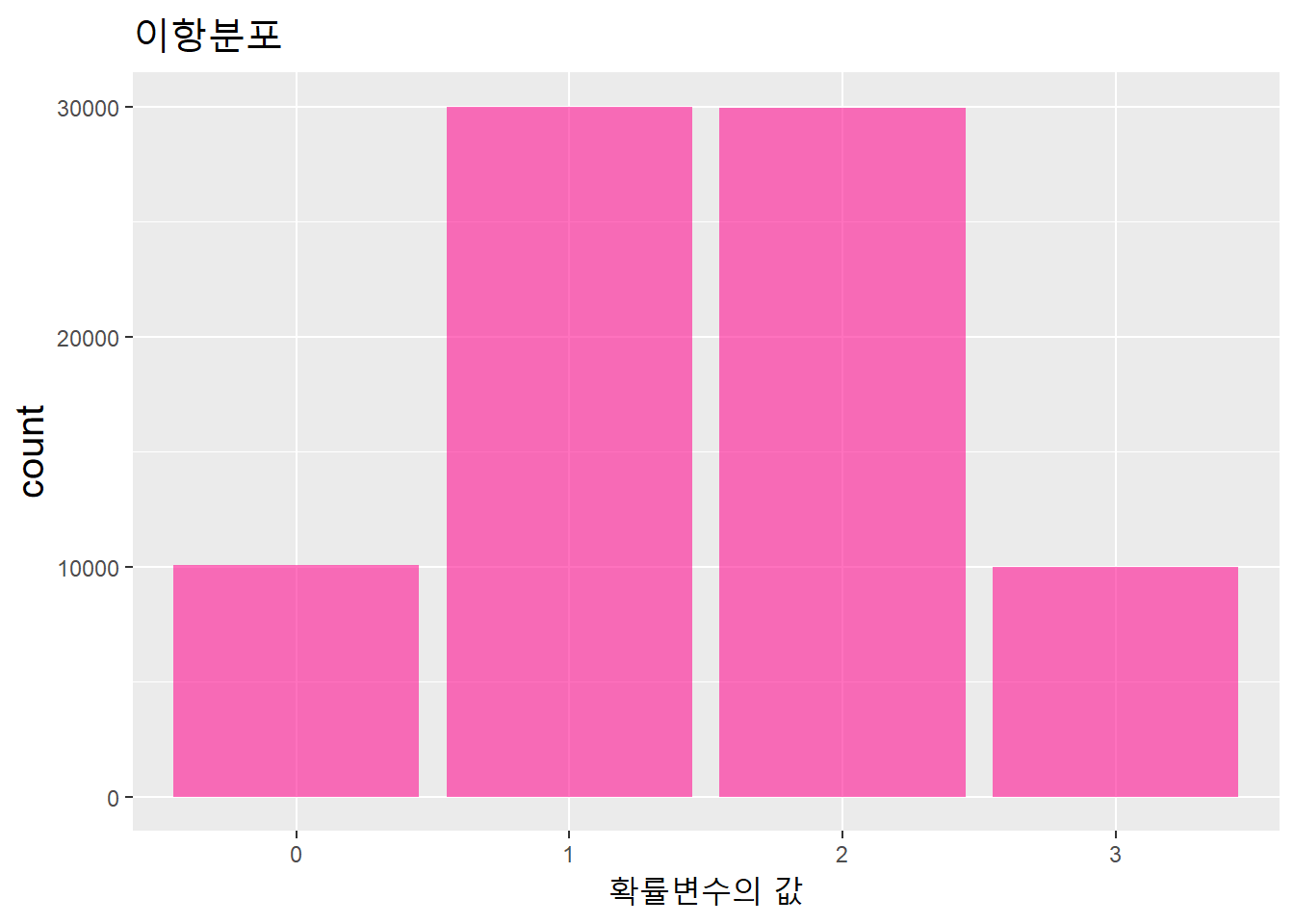

6.3.0.4 연속확률분포

연속확률분포의 확률은 확률변수의 값이 특정 값을 갖는 확률이 아니라, 값과 값 사이에 있을 확률이다. 즉, 특정 확률변수의 값에 대한 확률이 아니라 값과 값 사이의 구간에 대한 확률이다. 균등분포(uniform distribution)와 정규분포(normal distribution)가 대표적인 연속확률분포다.

균등분포: 각 구간 내의 값이 나타날 가능성이 동일한 분포

data.table(x = runif(80000, min = 0, max = 100)) %>% 
  ggplot(aes(x)) +
  geom_histogram(fill = "purple", color = "pink", 
                 alpha = .6, bins = 10) +
  labs(title = "균등분포",
       x = "확률변수의 값") +
  theme(title = element_text(size = 15))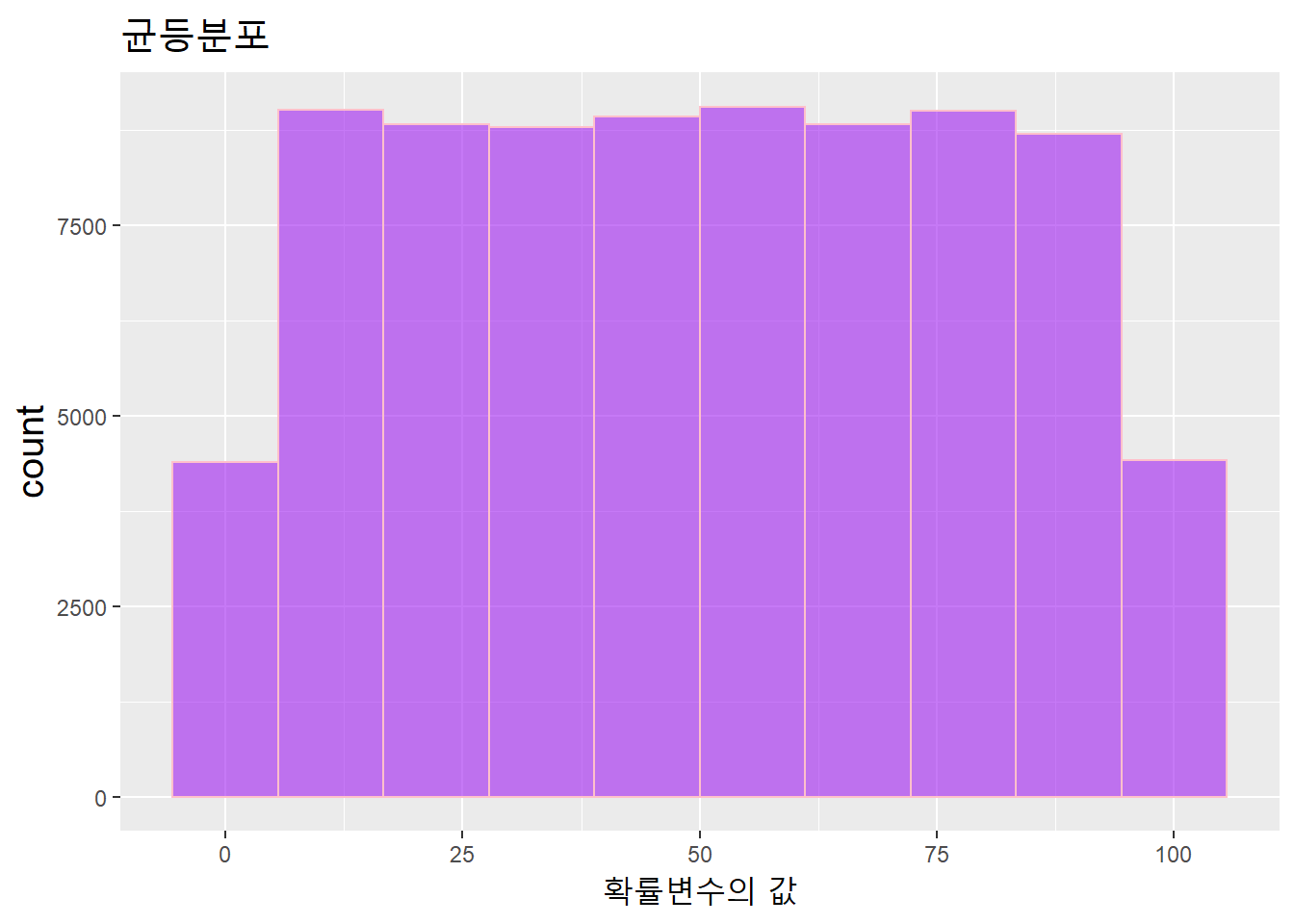

정규분포:

봉우리가 하나이고 좌우 대칭인 종모양의 곡선을 이루는 연속확률분포다. 정규분포는 평균(\(\mu\))과 표준편차(\(\sigma\))를 지정해 생성하므로 표기법은 다음과 같다. \(N\)은 정규(normal).

\[ N(\mu, \sigma^2) \]

정규분포를 생성하는 함수 rnorm(n, mean, sd)도 같은 원리다. \(N(50, 10^2)\)인 정규분포를 이루는 임의의 값 1000개는 다음과 같이 생성한다.

rnorm(1000, 50, 10)

표준편차를 달리한 정규분포를 2개 그려보자. 정규분포이므로 둘다 종모향의 좌우대칭 곡선이다.

m0sd1 <- rnorm(20000, 0, 1)
m19sd4 <- rnorm(20000, 19, 4)

m0 <- ggplot() + 
  geom_histogram(aes(m0sd1), binwidth = 0.25)
m19 <- ggplot() + 
  geom_histogram(aes(m19sd4), binwidth = 0.25)

m0 + m19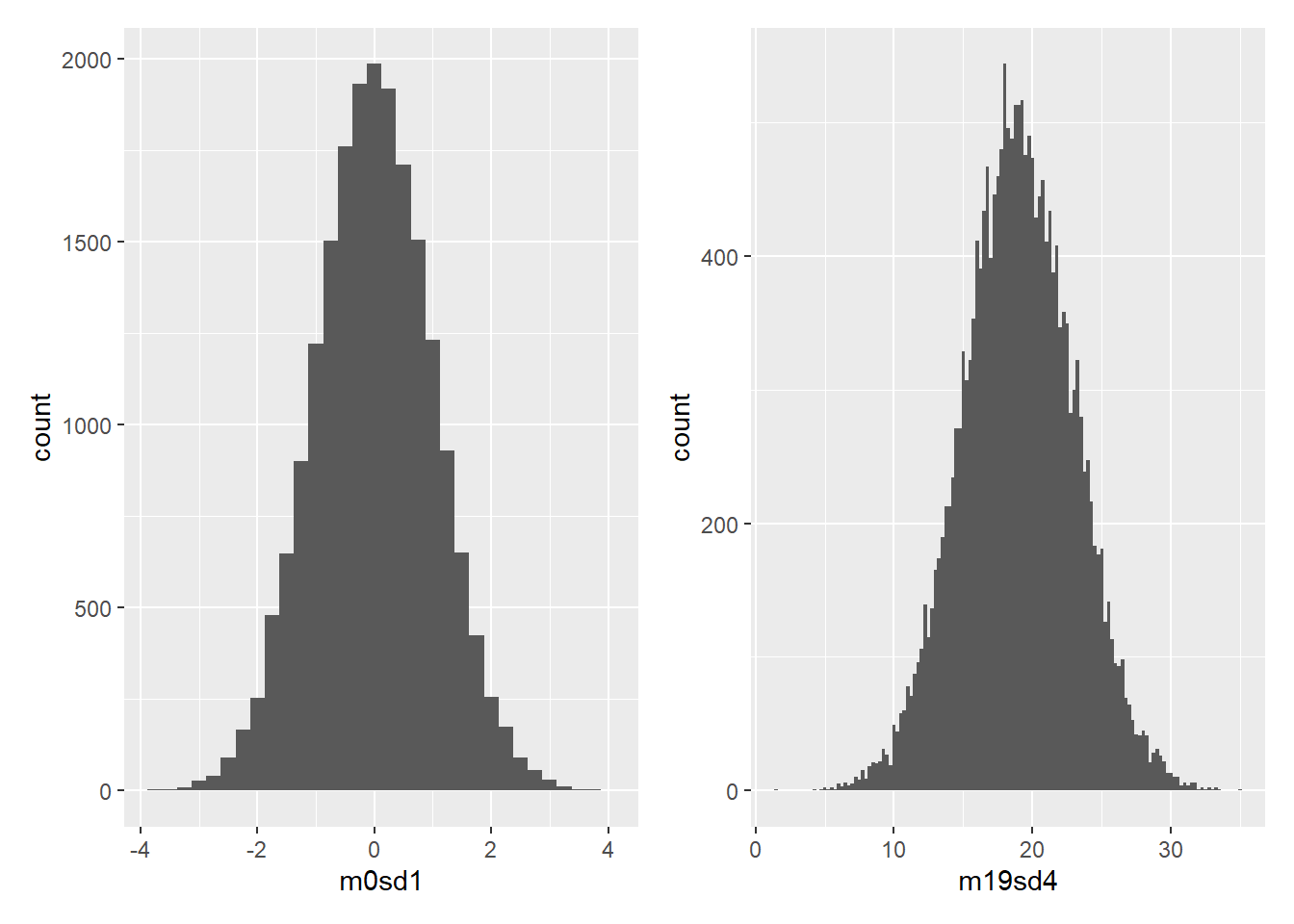

X축과 Y축을 일치시켜 보면 둘의 모양은 꽤 다르다. 표준편차가 작으면 높고 뾰족한 종모향의 분포를 만들고, 표준편차가 크면 낮고 납작해진다. 표준편차는 평균에서 자료가 벗어난 정도이므로, 표준편차가 클수록 값이 더 퍼지고, 표준편차가 작을수록 값이 평균을 중심으로 모인다.

m0sd1 <- rnorm(20000, 0, 1)
m19sd4 <- rnorm(20000, 19, 4)
df <- data.frame(
  cond = factor(rep(c("M:0, SD:1","M:19, SD:4"), 
                    each = 20000)),
  dist = c(m0sd1, m19sd4))

ggplot(df, aes(x = dist, fill = cond)) +
  geom_histogram(binwidth = .25)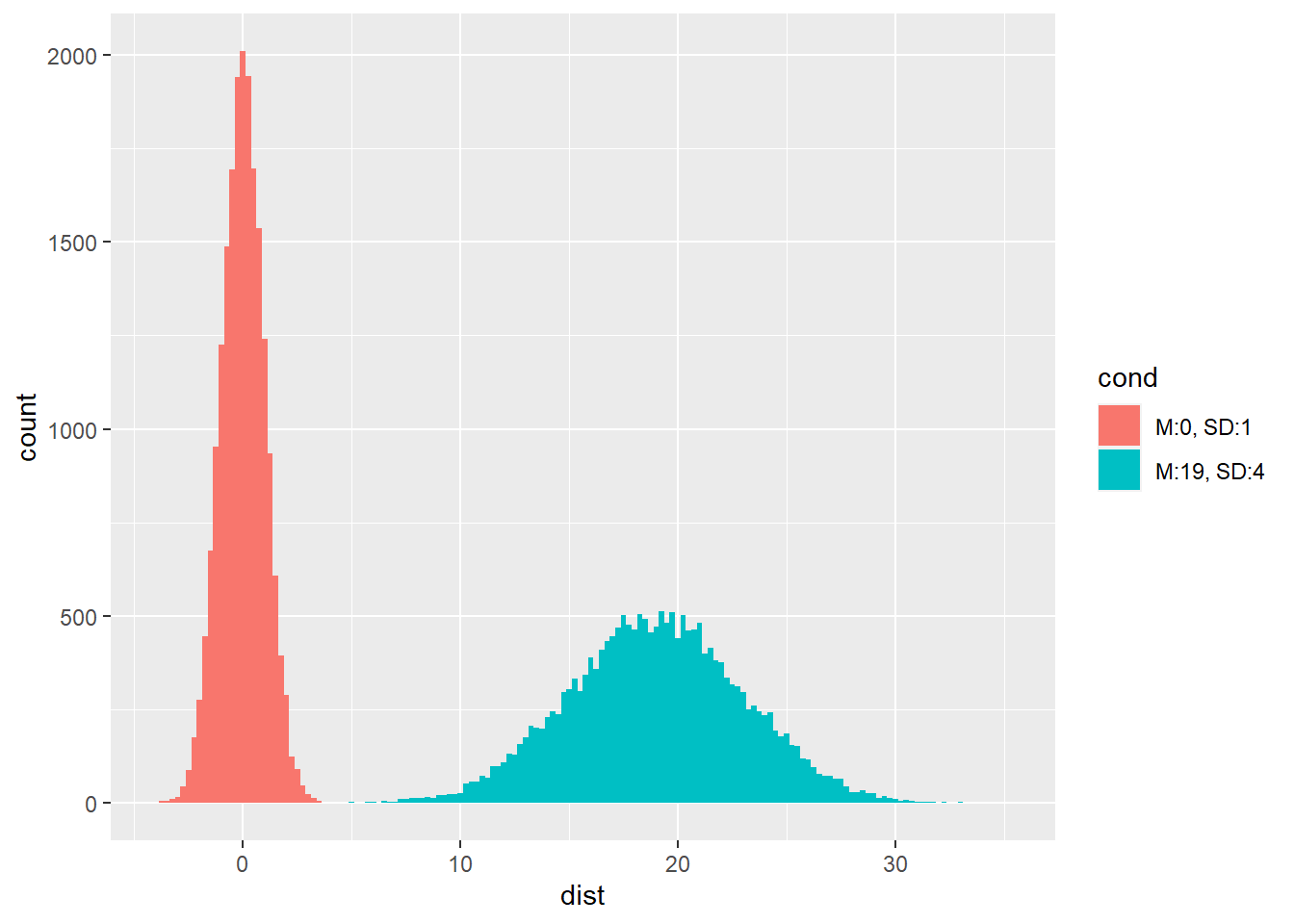

평균이 0이고, 표준편차가 1인 정규분포를 표준정규분포라고 한다.

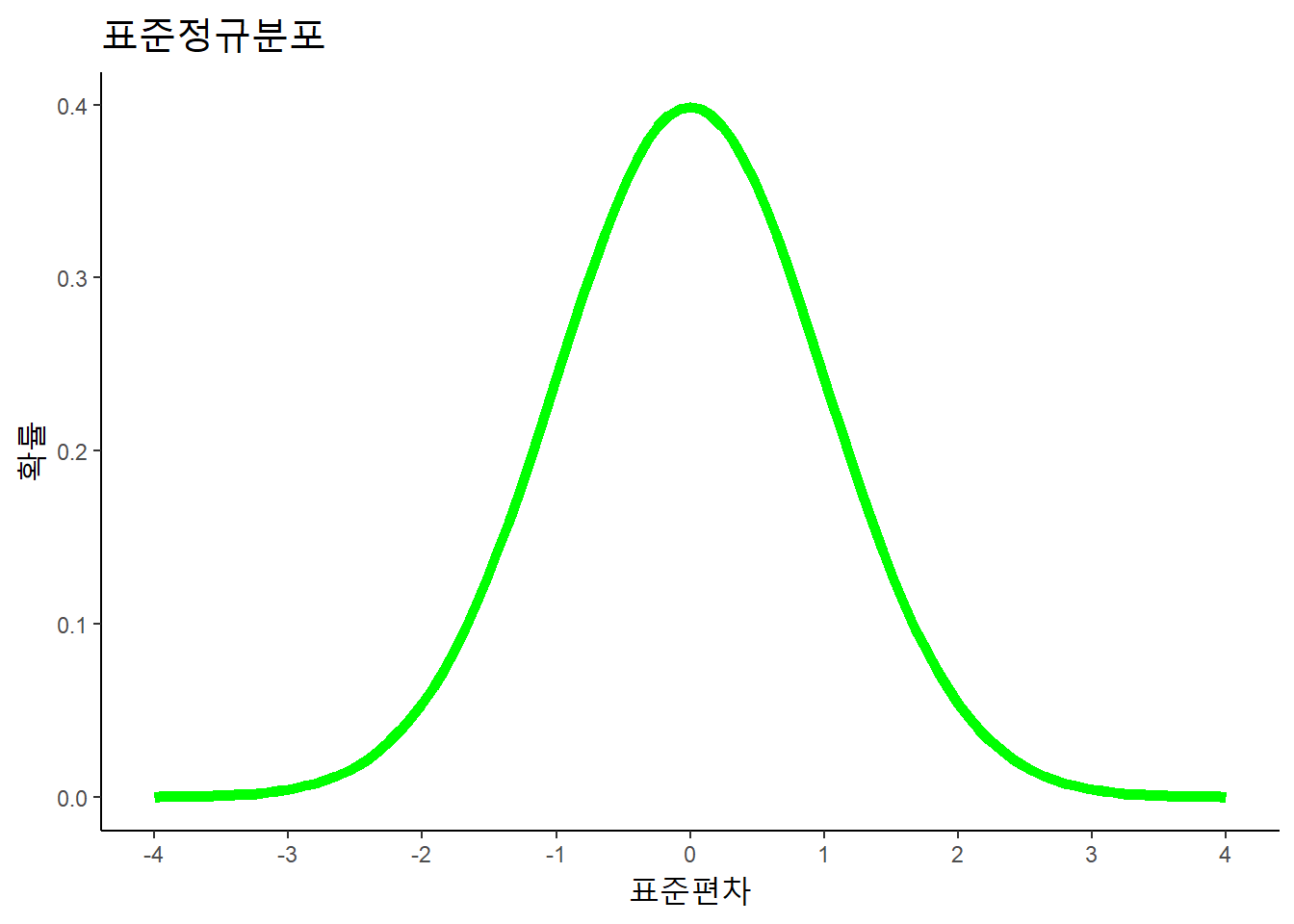
자료가 정규분포를 따르는 분포인 경우, 약 68%가 1표준편차 안에, 95%가 2표준편차 안에, 그리고 99.7%는 3표준편차안에 있다. 표준편차가 10이면 \(평균-10\)과 \(평균+10\) 사이에 자료의 68%가 있고, \(평균-20\)과 \(평균+20\) 사이에 95%가 있고, \(평균-30\)과 \(평균+30\) 사이에 99.7%가 있다 (Figure 6.2).

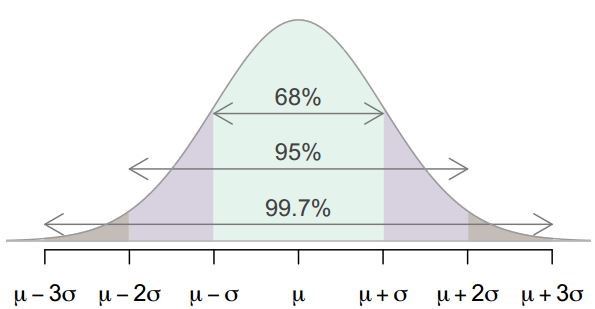
Figure 6.2: 68 - 95 - 99

6.3.0.5 표본분포(sampling distribution)

표집할 때마다 통계치가 매번 달라지나, 표집을 여러번 하면 표본이 여러개 생기고, 각 표본마다 통계치가 산출되므로, 그만큼 표본 통계치도 여러 개 생긴다. 즉, 표본의 통계치가 분포를 이루게 된다.

예를 들어, 표본을 1000번 표집하면 표본평균이 1000개 생성되면서, 1000개의 표본평균으로 이뤄진 표본평균의 분포를 만들 수 있다.

갑돌이가 활동중인 저그마을의 저그 인구가 1만명이라고 가정하고 가상의 모분포를 만들자.

set.seed(73)
population_v <- rnorm(n = 10000, mean = 50, sd = 10) %>% as.integer()
mean(population_v)

## [1] 49.4708

표본의 크기가 50개인 표본을 1000번 표집해 표본 1000개의 평균을 구한 다음, 표본 1000개 평균의 최소값, 1분위값, 중간값, 평균, 3분위값, 및 최대값을 구해보자.

set.seed(947)
# 표본의 갯수
nn <- 1000
# 표본의 크기
sample_size <- 50
sample_mean <- vector("integer", nn)
for(i in 1:nn){
  smp <- sample(population_v, sample_size, replace = T)
  sample_mean[i] <- mean(smp)
}
sample_mean -> sample1000_mean
head(sample1000_mean, 7)

## [1] 48.58 51.30 51.42 48.58 51.14 51.56 51.44

summary(sample1000_mean)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   44.70   48.46   49.38   49.39   50.33   53.70

표본크기가 50개인 표본을 각각 25회, 50회, 100회, 10000회 표집해 각 표본평균의 평균을 구한 다음, 표본1개 및 모집단의 평균과 비교해보자. 표본을 여러번 표집해 평균을 구할 때 표본 평균의 평균이 모집단의 평균과 비슷해 진다.

set.seed(73)
population_v <- rnorm(n = 10000, mean = 50, sd = 10) %>% as.integer()
sample_v1 <- sample(population_v, size = 50, replace = T)

# 표집 사용자 함수
sample_mean_f <- function(sample_size, sampling_nn) {
  sample_mean <- vector("integer", sampling_nn)
  for (i in 1:sampling_nn) {
    smp <- sample(population_v, sample_size, replace = T)
    sample_mean[i] <- mean(smp)
  }
 return(sample_mean) 
}
sample_mean_f(sample_size, 25) -> sample25_mean

# 표집 4회 반복
set.seed(811)  
sample_size <- 50
nn <- c(25, 50, 100, 10000) #표집 회수
op <- list()
for(i in 1:length(nn)){
  vv <- sample_mean_f(sample_size, nn[i])
  op <- list(op, vv)
}

# 데이터프레임으로 구성
data.frame(
  모평균  = mean(population_v),
  `표본1개 평균`  = mean(sample_v1),
  `표본25개 평균의 평균`  = mean(op[[1]][[1]][[1]][[2]]),
  `표본50개 평균의 평균`  = mean(op[[1]][[1]][[2]]),
  `표본100개 평균의 평균`  = mean(op[[1]][[2]]),
  `표본10000개 평균의 평균`  = mean(op[[2]])
) %>% 
  pivot_longer.(cols = everything(), 
                names_to = "-",
                values_to = "평균") %>% 
  gt() %>% 
  tab_header("표본의 평균의 평균") %>% 
  fmt_number(2, decimals = 2) %>% 
  tab_options(
    table.width = pct(50)
  )

표본의 평균의 평균
-	평균
모평균	49.47
표본1개.평균	51.84
표본25개.평균의.평균	49.24
표본50개.평균의.평균	49.65
표본100개.평균의.평균	49.39
표본10000개.평균의.평균	49.48

큰수의 법칙(law of large numbers):

표본크기가 증가함에 따라 표본평균이 모집단의 평균 또는 기댓값(expected value)에 수렴.

중심극한정리(central limit theorem):

표본크기가 증가함에 따라 표본평균의 분포가 정규분포에 수렴.

표본평균의 분포(표본 25개, 50개, 100개)를 히스토그램으로 그려보자.

hist_f <- function(xx, nn){
 p <- ggplot() + xlim(44, 56) +
  geom_histogram(aes_string(xx), binwidth = .5,
                 alpha = .5, color = "grey", fill = "deeppink") +
  labs(title = str_glue("표집 {nn}회")) 
  return(p)
}

options(scipen = 1) # 음수: scientific notation
nn <- c(25, 50, 100)
p <- list()
for(i in 1:length(nn)){
  p[[i]] <- hist_f(sample_mean_f(sample_size, nn[i]), nn[i])
}

p[[1]] + p[[2]] + p[[3]] +
  plot_annotation("표본평균의 분포") &
  theme(plot.title = element_text(size = 15))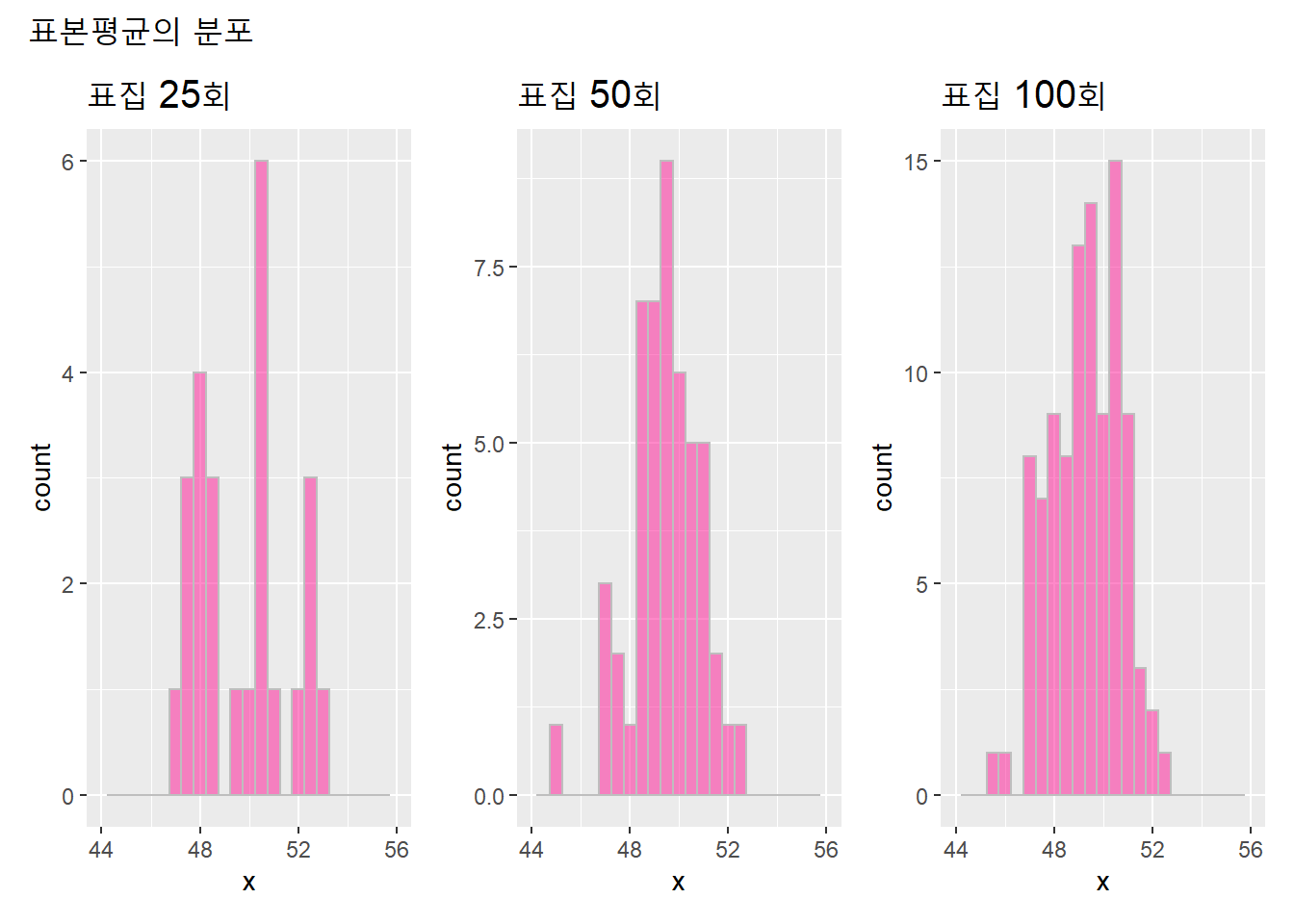

표본평균의 분포(100개, 10000개)를 히스토그램으로 그려보자. 표집을 여러번하여 표본의 갯수가 많을수록 정규분포와 유사해지며, 표본평균이 모평균에 수렴한다.

options(scipen = 1) # 음수: scientific notation
nn <- c(100, 10000)
p <- list()
for(i in 1:length(nn)){
  p[[i]] <- hist_f(sample_mean_f(sample_size, nn[i]), nn[i])
}

p[[1]] + p[[2]] +
  plot_annotation("표본평균의 분포") &
  theme(plot.title = element_text(size = 15))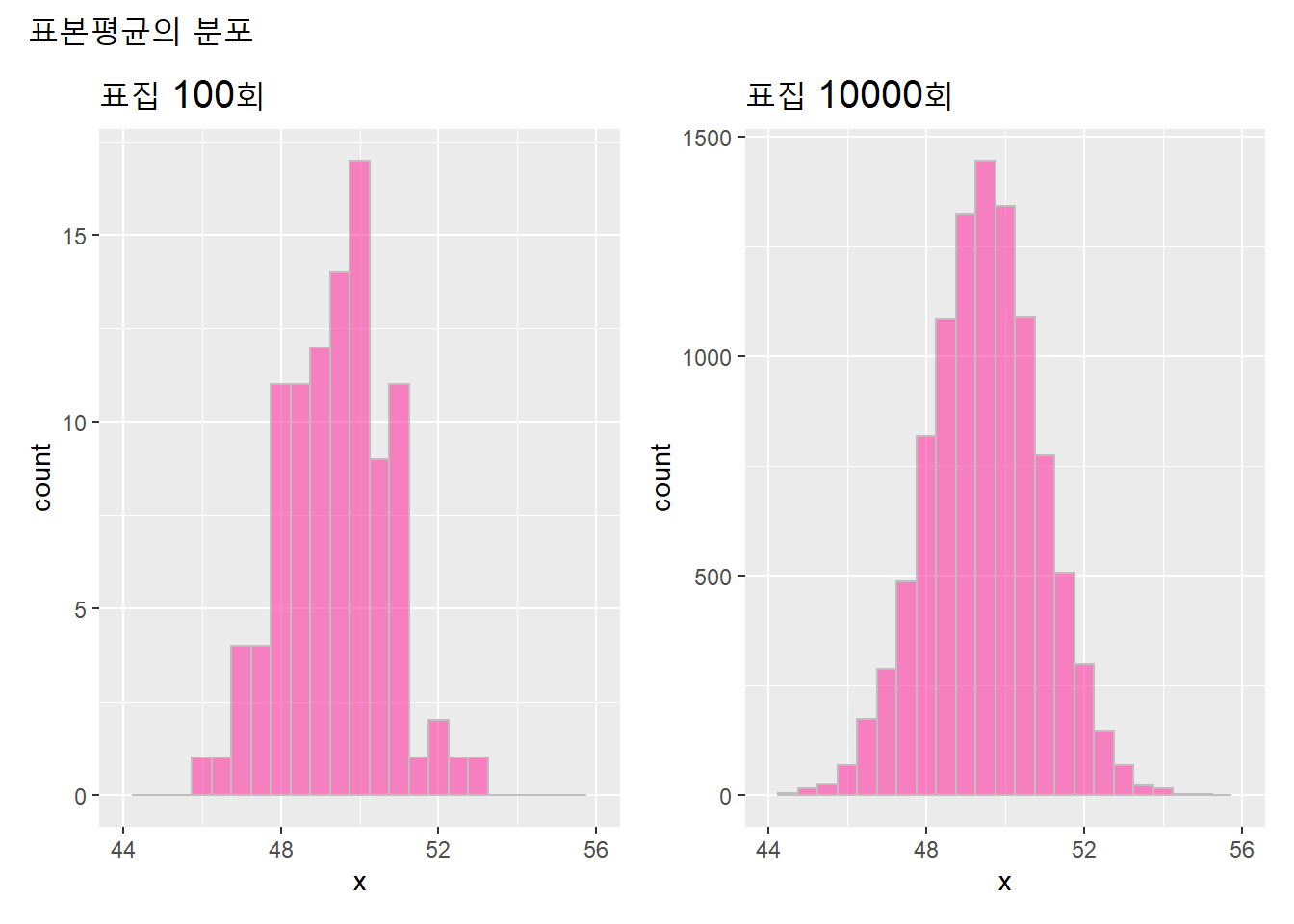

6.4 신뢰구간

6.4.1 표준오차

추정에는 두가지가 있다: 점추정(point estimation)과 구간추정(interval estimation).

점추정(point estimation): 표본의 통계치의 값 하나(점)를 모집단의 모수치로 추정. 예를 들어, 한국인 500명을 표집해 구한 수명(예: 84세)의 표본평균을 한국인 전체의 수명인 모평균(예: 84세)으로 추정한다면 이는 점추정한것이다.
구간추정(interval estimation): 표본의 통계치의 값에 대한 범위(구간)를 지정해 모집단의 모수치가 그 범위 안에 있을 것으로 추정. 예를 들어, 한국인 500명을 표집해 구한 수명의 표본평균(예: 84세)으로 한국인 전체 수명의 범위(예: 82세 ~ 86세)로 추정한다면 이는 구간추정한것이다. 구간추정을 하기 위해서는 표준오차(SE: standard error)를 알아야 한다.

표준오차는 일종의 표준편차(standard deviation)로서 표본분포의 추정 표준편차다. 표본의 통계치가 모수치 추정값에서 벗어난 정도의 평균을 나타낸다. 즉, 표본의 평균과 모집단의 평균이 다른 정도.

\[ 표준오차(SE) = \frac{표준편차(S)}{\sqrt{표본크기(n)}} \]

모집단을 가상으로 만들어 표준오차에 대해 살펴보자.

갑돌이가 활동중인 저그마을의 저그 인구가 1만명이라고 가정하고 가상의 모분포를 만들자.

set.seed(73)
population_v <- rnorm(n = 10000, mean = 50, sd = 10) %>% as.integer()
mean(population_v)

## [1] 49.4708

저그 50명을 두번 표집해 모집단의 모수치를 두 표본의 통계치와 비교해보자. 표본의 통계치는 표집할 때마다 표본평균의 값이 달라지고, 모평균과도 다른 값이 나온다.

set.seed(127)
sample(population_v, size = 50, replace = T) -> sample_v1
set.seed(211)
sample(population_v, size = 50, replace = T) -> sample_v2
data.table(
  표본 = c("표본1", "표본2"),
  평균  = c(mean(sample_v1), mean(sample_v2)),
  표준편차 = c(sd(sample_v1), sd(sample_v2)),
  표준오차 = c(
    sd(sample_v1)/sqrt(length(sample_v1)),
    sd(sample_v2)/sqrt(length(sample_v2)))
  ) %>% gt() %>% 
  tab_header("표준오차 비교") %>% 
  fmt_number(-1, decimals = 2) %>% 
  tab_options(
    table.width = pct(50)
  )

표준오차 비교
표본	평균	표준편차	표준오차
표본1	47.74	9.50	1.34
표본2	51.84	11.15	1.58

6.4.2 신뢰구간 구하기

단일 표본의 평균값(점 추정치)이 모평균을 정확하게 반영한다고 할 수 없지만, 그 평균이 모평균의 일정 범위 내(구간 추정치)의 값을 반영한다고 추정가능하다. 이렇게 표본평균의 값을 모평균의 일정범위 내의 값이라고 추정하는 구간을 신뢰구간(CI: confidence interval)이라고 한다.

신뢰구간(confidence interval): 신뢰추정치(confidence estimate)의 최대값과 최소값 사이

신뢰구간은 표준오차를 이용해서 추정한다.

신뢰구간의 최소값: 점 추정치에서 SE를 뺀 값
신뢰구간의 최대값: 점 추정치에서 SE를 더한 값

모평균을 추정하면서 이렇게 구간으로 추정하는 이유는 표본평균을 모평균으로 추정하는 과정에서 일정부분 오차가 발생할 수 밖에 없기 때문이다. 이 오차의 한계를 구간으로 지정하는 것이 신뢰구간. 신뢰구간의 최대값 혹은 신뢰구간의 최소값은 오차를 허용하는 한계라고 할 수 있다. 점추정치에서 신뢰구간의 최대값 혹은 최소값까지를 오차한계 또는 허용오차라고 한다 (Figure 6.3).

Figure 6.3: 신뢰구간

정규분포를 배울 때 다뤘던 68-95-99.7 규칙에 따르면, 정규분포의 약 68%는 평균의 1SD 상하 사이, 약 95%는 평균의 2SD 상하 사이, 약 99.7%는 평균의 3SD 상하 사이에 있다.

표본평균에 68-95-99.7 규칙을 적용하면 다음과 같다.

빈도의 약 68%(0.68확률)이라면,
- 표본평균은 모집단 평균에서 1표준오차 안에 있다.
빈도의 약 95%(0.95확률)이라면,
- 표본평균은 모집단 평균에서 2표준오차 안에 있다.
빈도의 약 99.7%(0.997확률)이라면,
- 표본평균은 모집단 평균에서 3표준오차 안에 있다.

저그마을의 갑돌이 상황을 이용해 구간 추정하는 연습 해보자. 갑돌이는 저그들의 면대면 대인커뮤니케이션에 대해 연구하기 시작했다. 남녀 저그 사이의 친밀한 관계가 연구주제다. 이 관계를 연구하기 위해 성인 저그 50명을 표집해서 이제까지 사귀었던 연인의 수를 조사했다. 조사 결과 평균적으로 3.2명을 사귄 것으로 나타났고 표준편차는 1.74다.

모평균의 구간을 추정하면?

이 문제를 풀기에 앞서서 여기서 모집단은 무엇일까?

모집단은 연구대상, 표본은 측정대상이므로, 모집단은 모든 성인저그다.

표준오차를 구한다.

\[ SE = \frac{S}{\sqrt{n}} \]

s_zg <- 1.74
n_zg <- 50
se_zg <- s_zg/sqrt(n_zg)

점추정치(표본평균)에서 표준오차를 더하고 빼 신뢰구간의 최대값과 최소값을 구한다. 일반적으로 구하는 신뢰구간이 표본평균 분포의 95%인 경우이므로 여기서는 2표준오차 구간을 계산한다.

m_zg <- 3.2
data.table(
  신뢰구간최소값 = m_zg - se_zg * 2,
  신뢰구간최대값 = m_zg + se_zg * 2
) %>% gt() %>% 
  fmt_number(1:2, decimals = 2)

신뢰구간최소값	신뢰구간최대값
2.71	3.69

2.7이 신뢰구간 최소값, 3.7이 신뢰구간 최대값. 따라서 모집단 평균의 구간은 2.7과 3.7이다.

앞서 추정한 모집단 평균의 구간[2.7, 3.7]에 대해 95%수준에서 신뢰(confident)할 수 있다고 할 때 , 신뢰구간[2.7, 3.7]에 대해 올바른 설명은 무엇일까?

이 표본에 있는 성인이 사귄 사람의 수는 2.7과 3.7사이
성인이 사귄 사람의 수는 2.7과 3.7사이
무작위로 성인을 선택했을 때, 그 사람이 사귄 사람의 수는 2.7과 3.7사이
95%의 성인이 사귄 사람의 수는 2.7과 3.7사이

답은 2번.

95% 신뢰구간[2.7, 3.7]의 의미는 무엇일까?

95%신뢰할 수 있는 수준에서 모집단의 평균값이 2.7과 3.7사이에 있다 는 의미인데, 여기서 95%신뢰할 수 있는 수준이라는 것은 표집분포에서 표본평균의 95%가 모평균의 추정구간에 포함된다는 것.

예를 들어 표본을 25개 표집했다고 할때, 25개 표본 중 24개의 표본 즉 표집한 전체의 표본 25개 중에서 95%( = 24/25)가 모평균 추정 구간에 포함돼 있다는 의미.

표본평균 24개(95% = 24/25)가 모평균 추정구간에 포함됐다는 것은 표집한 표본이 특이하지 않고, 일반적일 가능성이 95%.

표본평균 1개(5% = 1/25)는 모평균 추정구간에 포함되지 않았다는 것은 표집한 표본이 특이할 가능성이 5%.

즉, 95% 신뢰할 수 있는 수준이라는 것은 표본을 100번 표집한다고 했을 때 표본 95개는 그 표본평균의 신뢰구간으로 추정한 구간안에 모평균이 포함된다는 것이고, 표본 5개는 그 표본평균의 신뢰구간으로 추정한 구간안에 모평균이 포함되지 않는다는 것.

간단히 말해서 신뢰수준 95%라는 것은 표집한 표본에서 측정한 어떤 특성이 모집단에 그 특성이 있기 때문에 나타났을 확률이 95%, 표본이 특수하기 때문에 나타났을 가능성이 5%라는 것.

6.4.2.1 신뢰도와 정밀도

표본평균의 신뢰수준을 높이면(예: 68% → 95%) 모평균 추정의 정밀도는 올라갈까, 내려갈까?

신뢰도를 높이면 정밀도는 내려간다.

즉, 68%의 신뢰수준과 95% 신뢰수준 중 더 정밀한 추정은 68% 신뢰수준이다.

68%의 신뢰수준과 95% 신뢰수준 중 어느 것의 신뢰구간(CI: Confidence Interval)이 더 넓을까? 95% 신뢰수준이다.

신뢰도와 정밀도는 반비례 관계다 (Figure 6.4).

추정하는 구간이 바로 신뢰구간인데, 신뢰구간의 범위를 정하는 것이 신뢰수준. 95%의 신뢰수준이라고 한다면 그 구간이 점추정치에서 2표준오차 아래 위의 값 범위내에 있다. 반면 68%의 신뢰수준이라고 한다면 그 구간이 점추정치에서 1표준오차 아래 위의 값 범위내에 있다.

따라서 68%의 신뢰수준으로 모평균 구간을 추정하는 것이 95%의 신뢰수준으로 모평균 구간을 추정하는 것보다 더 정밀한 추정이라고 할 수 있다. 달리 말해, 68%의 신뢰수준으로 모평균 구간을 추정할 경우, 95% 신뢰수준보다는 정밀하게 모평균 구간을 추정할 수 있지만, 대신 신뢰도는 그만큼 떨어지게 된다.

Figure 6.4: 신뢰도와 정밀도

6.5 종합

6.5.1 통계

진양성
위양성
위음성
위양성
통속과학
체계적 과학
인과추론의 근본문제
무작위대조시험(RCT)
모수치(parameter)
통계치(statistic)
전수조사(census)
표집(sampling)
시행
표본공간
사건
복원추출
비복원추출
표집오차
확률변수
이산확률변수
베르누이확률변수
연속확률변수
이항분포
연속확률분포
균등분포
정규분포
표본분포
큰수의 법칙
중심극한정리
신뢰구간
표준오차
점추정
구간추정
표준오차

References

안도현. 2021. “유령위험과 무시된 위해: 위험의 개념화와 유형화.” 언론정보연구 58 (2): 5–65.